 |
Как решать уравнения? Тождественные преобразования.
|
|
|
|
В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой «х». Решить уравнение - это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.
Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.
1. Линейные уравнения. Это уравнения, в которых есть только неизвестные в первой степени, да числа. Причём в уравнении нет дробей с делением на неизвестное, это важно! А деление на число, или дробь числовая – это пожалуйста! Например:
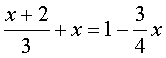
Это линейное уравнение. Здесь есть дроби, но нет иксов во второй, третьей и т.д. степени и нет иксов в знаменателях, т.е. нет деления на икс. А вот уравнение

нельзя назвать линейным. Здесь иксы все в первой степени, но есть деление на выражение с иксом. После упрощений и преобразований может получиться и линейное уравнение, и квадратное, и всё, что угодно.
В общем виде любое линейное уравнение сводится к виду:
ax + b = 0
Здесь b – любое число. Совсем любое. Дробь, целое, отрицательное, ноль и т.д. А а – любое, кроме нуля. Кстати, сообразите, почему так? Почему а не может быть нулём?
Если вы из запутанного и длинного уравнения путём упрощений, приведения подобных, промежуточных вычислений пришли к виду ax + b = 0, можно вздохнуть свободно. Как решать уравнение дальше - уже понятно. С иксами влево, без иксов - вправо... Помните это заклинание?)
|
|
|
2. Квадратные уравнения. Если в уравнении есть неизвестное в квадрате, уравнение называется квадратным. Кроме этого, в нём может быть (а может и не быть) просто икс (неизвестное в первой степени), всякие числа и коэффициенты и нет дробей с делением на неизвестное. Ну и, конечно, нет иксов в третьей, четвёртой и т.д. степенях. Например:

Любое квадратное уравнение сводится к виду:

Здесь a, b и с – тоже числа. b и c – совсем любые, а а – опять не равно нулю. Почему? Подставьте вместо а ноль. У нас исчезнет квадрат неизвестного! Уравнение станет линейным. Иначе уже решается…
Здесь та же песня, что и в линейных уравнениях. Если, после всяких упрощений и преобразований, вы получили уравнение вида
 ,
,
можно не волноваться. Как решать это уравнение дальше - уже понятно. А если непонятно, читайте следующий урок - и всё поймёте!
3. Дробные рациональные уравнения. Если в уравнении есть дроби с иксом в знаменателе, уравнение называется дробным рациональным, или просто дробным. Уравнение, что я приводил выше:

как раз - дробное.
Чтобы решать эти уравнения, надо уметь сводить их к первым двум типам. Это будет в отдельном уроке.
4. Все остальные уравнения. Этих больше всего, да… Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем.
Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.
И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные - третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, просто для них нет единой надежной и безотказной технологии. Приходится всякий раз как-то изворачиваться.
|
|
|
Но для линейных и квадратных такая технология есть. Если уж мы добрались до выражений вида ax + b = 0, или
 ,
,
то решим их наверняка. Если добрались…
Это и есть самое интересное. Как хитрое исходное уравнение привести к приличному (т.е. вполне решаемому) виду?
Я выше писал про всякие упрощения и преобразования. Именно здесь и зарыты всякие ошибки и подводные камни. Разберёмся с этим.
В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходное выражение. Причем так, чтобы при смене внешнего вида суть выражения не менялась. Такие преобразования называются тождественными или равносильными.
|
|
|


