 |
Тождественные преобразования.
|
|
|
|
Сейчас мы с вами повторим все-все-все базовые тождественные преобразования.
Их два.
Базовые потому, что их можно применять к любым уравнениям – тригонометрическим, показательным, иррациональным и т.д. и т.п.
Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое, но одно и то же число или выражение (в том числе и выражение с неизвестным!). Вы постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа:

Дело знакомое, переносим 2 вправо, и получаем:
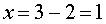
На самом деле вы отняли от обеих частей уравнения 2:


И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах…. Это в разделе на четвёрку. Загляните, там просто всё!
Второе тождественное преобразование: обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа

Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. Ещё уравнение, чуть похитрее:

Здесь кое-кто и запутается…. Озарение не наступит, а делить обе части на дробь 1/5 не очень в уме удобно… Чтобы не опозориться на ровном месте, нужно просто сказать себе: слева нам нужен чистый х. Нам мешает дробь 1/5. Чтобы избавиться от неё, надо левую часть поделить на 1/5. Или, что проще, умножить на 5. Или на дробь 5/1, это всё едино. Это нам надо. Чтобы пятёрки сократились, и остался чистый х. А математике надо, чтобы вы тогда уж и правую часть умножили на 5. Тогда всем будет хорошо:
|
|
|
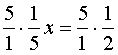

Умножение обеих частей на нужное число, позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, вполне можно и ошибок наляпать. Короче дорога – меньше ошибок!
Вот и всё.
Забавно, но эти два (всего два!) действия с уравнениями решают кучу проблем! Если их делать правильно, разумеется. Посмотрим, как эти тождественные преобразования применяются на практике. Для начала решим простенькое уравнение:

Это линейное уравнение. С чего начнём? Задаю вам ключевой вопрос: что вам больше всего не нравится в этом уравнении?
95 человек из 100 ответят: дроби! Ответ правильный. Вот и давайте от них избавимся. Здесь нам пригодится второе тождественное преобразование. На что нужно умножить дробь слева, чтобы знаменатель сократился напрочь? Верно, на 3. А справа? На 4. Но математика позволяет нам умножать обе части на одно и то же число. Как выкрутимся? А умножим обе части на 12! Т.е. на общий знаменатель. Тогда и тройка сократится, и четвёрка. Не забываем, что умножать надо каждую часть целиком. Вот как выглядит первый шаг:
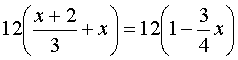
Раскрываем скобки:

Обратите внимание! Числитель (х+2) я взял в скобки! Это потому, что при умножении дробей, числитель умножается весь, целиком! А теперь дроби и сократить можно:

Раскрываем оставшиеся скобки:

А теперь – одно удовольствие! Вспоминаем заклинание из младших классов: с иксом – влево, без икса – вправо!
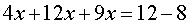
Приводим подобные:

И делим обе части на 25:

Вот и всё. Ответ: х =0,16
Берём на заметку: чтобы преобразовать исходное замороченное уравнение к приятному виду, мы использовали два (всего два!) тождественных преобразования – перенос влево-вправо со сменой знака и умножение-деление уравнения на одно и то же число. Это универсальный способ! Работать таким образом мы будем с любыми уравнениями! Совершенно любыми. Но на этой страничке потренируемся с простыми линейными уравнениями.
|
|
|
А на ЕГЭ они будут? - слышу вопрос практичных людей. Отвечаю. В чистом виде - нет. Слишком элементарны. А вот при решении задачек в ЕГЭ вы с ними столкнётесь обязательно! Так что, меняем мышку на ручку и решаем.




Ответы даны в беспорядке: 2,5; нет решений; 51; 17.
Напомню, что если вам в примере встречаются целые и смешанные числа, десятичные дроби, – превращаем их в обыкновенные дроби, и – вперёд! Как описано в разделе "Дроби".
А как решать уравнения более хитрые, - это в следующей теме.
|
|
|


