Подходы к выбору оптимального портфеля

 

Существует несколько подходов к выбору наиболее оптимального для инвестора портфеля активов.

Теория портфеля (Г. Марковец)

 

 

Инвестор должен основывать свое решение по выбору портфеля исключительно на ожидаемой доходности и стандартном отклонении этого портфеля. Следовательно, инвестор должен оценить ожидаемую доходность и стандартное отклонение каждого портфеля, а затем выбрать лучший из них, основываясь на соотношении этих двух параметров.

Этот метод связан с построением кривых безразличия, которые отражают отношение инвестора к риску и доходности.

При использовании подхода Марковец делается предположение о ненасыщаемости, т.е. предполагается, что инвестор предпочитает более высокий уровень конечного благосостояния более низкому его уровню.

Когда инвестору необходимо выбирать между портфелями, имеющими один уровень доходности, но разный уровень отклонения, нужно принимать во внимание предположение, что инвестор избегает риска.

Эти два предположения о ненасыщаемости и избегании риска являются причинами выпуклости кривой безразличия и положительного наклона кривой.

Подход ожидаемой доходности актива

 

,

 

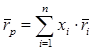где  – ожидаемая доходность портфеля;

x_i – доля начальной стоимости портфеля, инвестированная в актив i;

 – ожидаемая доходность финансового актива i;

n – количество ценных бумаг в портфеле.

 

 

Так как ожидаемая доходность портфеля представляет собой средневзвешенное ожидание доходности его активов, то вклад каждого актива в ожидаемую доходность портфеля зависит от его доходности и от его доли.

При расчете риска (σ_p) учитывается взаимосвязь между разными активами в портфеле и их рисками.

,

 

где x_i – доля в общей стоимости портфеля актива i;

x_j – доля в общей стоимости портфеля актива j;

cov_ij – ковариация доходности i и j активов.

 

,

 

где cor_ij – коэффициент корреляции между доходностью на ценную бумагу i и на ценную бумагу j.

- 1 ≤ cor ≤ 1

Если cor = 0, это говорит о некоррелируемой доходности.

 

Пример:

Пусть имеется портфель активов, состоящий из акций А, B, С

		r %			xi		Вклад в rp
А		16,2			0,2325		3,77
В		24,6			0,4070		10,01
С		22,8			0,3605		8,22
	А		В	С
А	146		187	145
В	187		854	104
С	145		104	289

Ранее было отмечено, что подход Марковеца предполагает избегание инвестором риска. Хотя это предположение является вполне резонным, оно не является необходимым. Вместо этого можно предположить, что инвестор азартен или нейтрален к риску. Для того, чтобы понять различия инвесторов, нужно ввести честную игру.

Честная игра – это игра, при которой по определению ожидаемое вознаграждение равно нулю.

Инвестор, который избегает риска, отказывается или не захочет выбрать игру. Это объясняется тем фактором, что количество разочарований при потенциальном проигрыше оказывается выше, чем количество удовольствия при потенциальном выигрыше.

Если азартный инвестор столкнется с честной игрой, он предпочтет принять участие в данном проекте.

Кроме того, крупные игры более привлекают, чем мелкие. Это означает, что при выборе двух портфелей, имеющих одинаковую доходность, инвестор выберет тот портфель, у которого больше стандартное отклонение.

Рисковый инвестор выбирает портфель выше и правее.

В случае нейтральности к риску инвестор находится между случаем избегания риска и азартности.

В то время как инвестор, избегающий риска, не хочет принимать участие в честной игре, а азартный инвестор – наоборот, хочет, нейтральному к риску инвестору все равно принимать участие в игре или не принимать. Это означает, что риск (стандартное отклонение) для него не имеет важного значения.

Кривые безразличия

 

Теория портфеля (Г. Марковец) связанас построением кривых безразличия, которые отражают отношение инвестора к риску и доходности.

 

	А	B	C	D
rp	8	12	11	7
σ p	10	20	13	17

 

Каждая кривая линия на графике отображает одну кривую безразличия и представляет все комбинации портфеля, которые обеспечивают заданный уровень желания инвестора.

Свойства кривых безразличия:

1. Все портфели, лежащие на данной кривой безразличия являются равноценными для инвестора.

2. Кривые безразличия не могут пересекаться, т.к. они отражают разные уровни желательности.

3. Инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, привлекательнее, чем любой портфель, лежащий на кривой безразличия, расположенный ниже и правее.

4. Как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними.

 

Предыдущая12345678Следующая

Поделиться:

Воспользуйтесь поиском по сайту: