 |
Диверсификация финансовых активов. Рыночный и собственный риск портфеля
|
|
|
|
Исходя из рыночной модели, общий риск финансового актива (σi2) состоит из двух частей:
- рыночный или систематический риск;
- собственный или несистемный риск.
,
где σi2 – общий риск финансового актива;
βiI2 σI2 – рыночный риск;
σεi2 – собственный риск.
Мерой собственного риска является дисперсия случайной погрешности.
Общий риск портфеля
Рассмотрим случай, когда доходность каждого рискового финансового актива из портфеля связана с доходностью рыночного индекса.
Доходность портфеля может быть определена как:
,
где хi – доля средств, вложенных в актив i;
N – количество финансовых активов.
- рыночная модель портфеля финансовых активов.
Данная модель является прямым обобщением рыночных моделей отдельных финансовых активов, входящих в его состав.
Общий риск портфеля измеряется дисперсией его доходности и обозначается σр2:
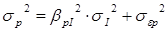
Он состоит из рыночного и собственного риска.
Увеличение диверсификации может привести к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля. В то время как рыночный риск портфеля остается примерно таким же.
Чем более диверсифицирован портфель, тем меньше каждая доля актива в нем. При этом значение βpI не меняется существенным образом, за исключением случаев преднамеренного включения в портфель финансовых активов с относительно низким или высоким значением βiI.
Поэтому диверсификация приводит только к усреднению среднего риска.
Иная ситуация при рассмотрении риска портфеля
Предположим, что во все финансовые активы инвестировано одинаковое количество средств, т.е. доля xi каждого финансового актива равна 1/N.
|
|
|
(средний собственный риск).
Собственный риск портфеля в N-раз меньше среднего собственного риска финансового актива.
Более диверсифицированный портфель – средний собственный риск практически не изменится.
Пример:
Первый портфель ценных бумаг состоит из 4-х ценных бумаг, второй – из 10. Все ценные бумаги имеют β = 1 и собственный риск = 30%. В обоих портфелях доля всех ценных бумаг одинакова. Вычислить общий риск каждого портфеля, если стандартное отклонение индекса рынка составляет 20%.
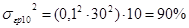
Оценка рисков безрисковых активов
Безрисковый активпредполагает, что доход по нему является определенным в конце инвестиционного периода.
Стандартное отклонение для безрискового актива рано нулю.
Ковариация между ставкой доходности по безрисковому активу и ставкой доходности по рисковому активу также равна нулю.
Т.е. безрисковые актив имеет фиксированный доход и нулевую вероятность неуплаты (государственные ценные бумаги).
При этом срок погашения совпадает с периодом владения, т.е. отсутствует неопределенность.
Такое инвестирование называется безрисковым кредитованием.
Появление новых возможностей при инвестировании существенно расширяет достижимое множество портфеля активов и изменяет расположение эффективного множества.
Рассмотрим ожидаемую доходность и стандартное отклонение для портфеля, состоящего из инвестиций в безрисковые активы в сочетании с одним рисковым активом.
Пример:
A, B, C + 1 безрисковый актив
х1 – доля актива
х4 = 1 – х1 – доля в безрисковом активе
| Портфели | х1 | х4 | rp | σ p |
| A | 0,00 | 1,00 | 4% | 0,0 |
| B | 0,25 | 0,75 | 7,05% | 3,02 |
| C | 0,5 | 0,5 | 10,10% | 6,04 |
| D | 0,75 | 0,25 | 13,15% | 9,06 |
Предположим, что х4 имеет ставку доходности 4%.
r4 = 4%
r1 = 16,2%
Любой портфель, состоящий из комбинации безрисковых и рисковых активов, будут иметь ожидаемую доходность и стандартное отклонение, которые лежат на одной прямой, соединяющей точки, соответствующие этим активам.
|
|
|
|
|
|
