 |
А теперь от теории принятия решений перейдём к матричным играм.
|
|
|
|
Матричная игра игроков с нулевой суммой может рассматриваться, как следующая абстрактная игра двух игроков.
Игрок А имеет m стратегий i = 1, 2, …, m. Игрок В имеет n стратегий j = 1, 2, …, n. Каждой паре стратегий (i, j) поставлено в соответствие число а 
, выражающее выигрыш игрока А за счет игрока В, если первый игрок примет свою i -ю стратегию, а второй – свою j -ю стратегию.
Каждый из игроков делает один ход: игрок А выбирает свою i -ю стратегию (i =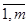 
), В – свою j -ю стратегию (j = 
), после чего игрок А получает выигрыш а за счет игрока А (если а < 0, то это значит, что игрок В платит второму сумму |а |). На этом игра заканчивается.
Каждая стратегия игрока i = 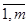или j = часто называется чистой стратегией.
Если рассмотреть матрицу А:
а 
| а 
| … | а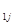 
| … | а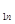 
|
| … | … | … | … | … | … |
а 
| а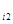 
| … | а
| … | а 
|
| … | … | … | … | … | … |
а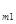 
| а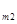 
| … | а 
| … | а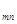 
|
то проведение каждой партии матричной игры с матрицей сводится к выбору игроком А i -й строки, а игроком В j -го столбца и получения игроком А (за счет игрока В) выигрыша а .
Как было сказано выше, главным в теории игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл: стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока.
Исходя из этих позиций, игрок А исследует матрицу выигрышей следующим образом: для каждого значения i (i =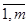 
) определяется минимальное значение выигрыша в зависимости от применяемых стратегий игрока В
а 
(i = )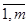
т.е. определяется минимальный выигрыш для игрока А при условии, что он примет свою i -ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i = i 
, при которой этот минимальный выигрыш будет максимальным, т.е. находится
|
|
|
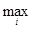
а = а 
= α
Определение игры
Дадим определение понятию «Игра». Игрой называется набор
,
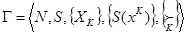где N – произвольное множество игроков; S – произвольное множество всех исходов игры; XK - произвольное множество стратегий коалиции K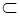 
N; S (XK) 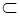S – множество возможных исходов, если коалиция K применяет стратегию х K 
Х K;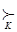 
- транзитивное отношение предпочтения коалиции K 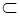N на S. При математической формализации игра, должна проходить по определенным правилам, которые представляют следующую систему условий:
- возможные действия каждого из игроков;
- объем информации, которую может получить каждая сторона о действиях другой;
- исход игры в результате каждой совокупности ходов противников.
Игроки: Считается заданным список игроков. Если игроков различать по номерам, то их список сводится к множеству 
, где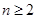 
- число игроков. Считается, что игроки осведомлены о наличии каждого из своих партнеров.
Действия: Каждый игрок 
имеет в своём распоряжении некоторый набор стратегий 
. Множества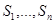 
могут быть как конечными, так и бесконечными. В основе рационального поведения участников игры лежит так называемый постулат «общего знания»: каждый полностью информирован о своих стратегических возможностях и о стратегических возможностях своих партнёров. Процесс игры состоит в выборе каждым из игроков своей стратегии: 
. В результате складывается игровая ситуация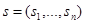 
. Множество Ω всех возможных игровых ситуаций образует ситуационное пространство игры, обозначаемое 
.
Интересы: Степень заинтересованности игрока k в той или иной ситуации s определяется размером выигрыша 
, который в этой ситуации он может получить. Таким образом, правила игры получаются заданием так называемых, функций выигрыша 
. Эти функции принимают числовые значения и имеют общую область определения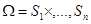 
. Каждая из таких функций есть функция «n-переменных»: 
.
|
|
|
Основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявление для каждого из них «оптимальной стратегии». Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или эквивалентно минимально возможный средний проигрыш).
Опишем некоторые основные понятия, используемые в теории игр. Заинтересованные стороны называются игроками. Любое возможное действие для игрока называется его стратегией. В условиях конфликта каждый игрок придерживается выбранной им стратегии, в результате появляется набор стратегий, называемый ситуацией. Заинтересованность игроков в каждой конкретной ситуации, проявляется в том, что каждому игроку в данной ситуации приписывается число, выражающее степень удовлетворённости его интересов. Такое число называется выигрышем.
Игра начинается с некоторого положения и состоит из последовательности личных ходов, при каждом из которых один из игроков совершает выбор среди нескольких возможностей. Некоторые ходы могут быть случайными (таковы, например, бросание кости или тасование колоды карт).
Примерами игр такого типа являются шахматы, в которых нет случайных ходов (кроме разыгрывания того, кто будет играть белыми), бридж, в котором случай играет большую роль.
На примере бриджа и шахмат можно показать другой важный элемент игры. Именно, в шахматной игре каждый игрок знает любой ход, который был сделан до этого момента, в то время как в бридже это знание игрока обычно неполно. Таким образом, в некоторых играх игрок не в состоянии определить, какой из нескольких возможных ходов был фактически сделан, будь то ход одного из его противников или случайный ход. На практике это означает, что, когда игрок делает свой ход, он не знает точной позиции игры и должен делать ход с учетом того, что имеется несколько возможных позиций.
В конце игры игроки обычно получают какой-либо выигрыш, (может быть в форме денег, престижа или иного удовлетворения), который зависит от протекания игры. В общее представление об игре входят 3 элемента:
|
|
|
1 чередование ходов, которые могут быть как личными, так и случайными
2 возможная недостаточность информации
3 функция выигрыша
Запишем теперь основные этапы поиска решения игры:
1 проверка наличия (или отсутствия) равновесия в чистых стратегиях (к этому вопросу вернёмся чуть позже). При наличии равновесной ситуации указываются соответствующие оптимальные стратегии игроков и цена игры.
2 поиск доминирующих стратегий (в случае успеха этого поиска – отбрасывание доминирующих строк и столбцов в исходной матрице игры).
3 замена игры на её смешанное расширение и отыскание оптимальных смешанных стратегий и цены игры.
| Игрок 2 стратегия 1 | Игрок 2 стратегия 2 | |
| Игрок 1 стратегия 1 | 4, 3 | –1, –1 |
| Игрок 1 стратегия 2 | 0, 0 | 3, 4 |
| Нормальная форма для игры с 2 игроками, у каждого из которых по 2 стратегии. | ||
Отметим, что нормальная форма антагонистической игры сводится к некоторой матрице А с числом строк равным числу стратегий игрока 1 и с числом столбцов, равным числу стратегий игрока 2. Выигрыш – если игрок 1 выбирает i-ю стратегию, а игрок 2 j-ю стратегию – представляет собой элемент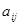 
в i-ой строке и в j-ом столбце данной матрицы.
Игроков, как участников игры, интересует, какие из стратегий являются выигрышными с точки зрения максимизации доли каждого игрока в выигрыше. Однако, результаты случайных ходов, известны только в вероятностном смысле, поэтому лучше рассматривать математическое ожидание функции выигрыша, определённое в случае, когда игроки используют n-набор стратегий. Поэтому для описания математического ожидания функции выигрыша, при условии, что игрок i применяет стратегию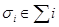 
, можно употребить следующее обозначение 
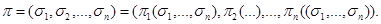Исходя из этого функцию 
на множестве всех возможных значений переменных 
можно выразить либо в форме соотношения, либо в виде n -мерной матрицы n -векторов. Такая n -мерная таблица называется нормальной формой игры Г. В нормальной (стратегической) форме игра описывается платёжной матрицей. Каждая сторона матрицы – это игрок, строки определяют стратегии первого игрока, а столбцы – второго. На пересечении двух стратегий можно увидеть выигрыши, которые получат игроки. На примере, если игрок 1 выбирает первую стратегию, а второй игрок – вторую, то на пересечении получится (1,-1). Это значит, что в результате хода игроки потеряли по одному очку.
|
|
|
Пример 1: игра «Орлянка».
| X \ Y | Орел | Решка |
| Орел | -1, 1 | 1, -1 |
| Решка | 1, -1 | -1, 1 |
Первый игрок прячет монету орлом или решкой вверх, а второй пытается угадать, как она спрятана. Если он не угадывает – платит первому одну денежную единицу, если угадывает – первый платит ему одну денежную единицу. В данной игре каждый игрок имеет две стратегии: «орёл» и «решка». Множество ситуаций в игре состоит из 4 элементов. В строках таблицы указаны стратегии первого игрока Х, в столбцах – стратегии второго игрока Y. Для каждой из ситуаций указаны выигрыши первого и второго игроков.
Рассмотрим основную теорему матричных игр.
Основная теорема теории матричных игр (по Дж. фон Нейману).
Для матричной игры с любой матрицей Авеличины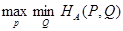 
и 
равны между собой, т.е.
Более того, существует хотя бы одна ситуация в смешанных стратегиях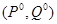 
, для которой выполняется соотношение
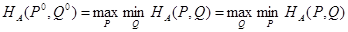
Иными словами, любая матричная игра имеет решение в смешанных стратегиях. Поиск этого решения опирается на установленные факты.
Приведём доказательство данной теоремы (автор: Дж. Б. Данциг, 1951г.)
Теорема. Каждая матричная игра с нулевой суммой всегда имеет решение в смешанных стратегиях, т.е. существуют такое число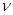 
и такие стратегии 
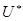и 
игроков 1 и 2 соответственно, выполняются неравенства:
. (*)
Комментарий. Формула (*) означает, что: если игрок 1 отклоняется от своей оптимальной стратегии, то его выигрыш не увеличивается по сравнению с ценой игры; если от своей оптимальной стратегии отклоняется игрок 2, то по сравнению с ценой игры его проигрыш не уменьшается.
Доказательство.
Пусть матрица игры равна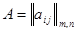 
. Всегда можно считать, что все коэффициенты 
. Если это не так, то предположим, что наименьший из всех отрицательных коэффициентов есть 
. Тогда увеличим все элементы платёжной матрицы на произвольное положительной число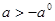 
. Функция выигрыша при этом окажется равной
.
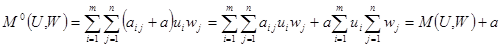Из этого следует, что от увеличения всех элементов матрицы 
на величину 
цена игры увеличивается на эту величину, причём оптимальные смешанные стратегии не изменяются.
Для определения среднего оптимального выигрыша игрока 1, соответствующего первоначальной платёжной матрице, необходимо из найденной цены игры вычесть величину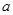 
.
|
|
|
Классификация игр
Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры. В зависимости от числа игроков различают игры с двумя, тремя и более участниками. Согласно другому принципу классификации (по количеству стратегий) различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий (например, в игре в орлянку игроки имеют по два возможных хода - они могут выбрать "орел" или "решку"). Сами стратегии в конечных играх нередко называются чистыми стратегиями (смысл этого названия будет ясен далее).
Соответственно, в бесконечных играх игроки имеют бесконечное число возможных стратегий. Так в ситуации «Продавец-Покупатель» каждый из игроков может назвать любую устраивающую его цену и количество продаваемого (покупаемого) товара. Третий способ классификации игр-по свойствам функции выигрыша (платежных функций). Важным случаем в теории игр является ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. налицо прямой конфликт между игроками. Подобные игры называются играми с нулевой суммой, или антагонистическими играми. Игры в орлянку или в шахматы - типичные примеры антагонистических игр. Прямой противоположностью играм такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща. Между этими крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков. Можно также выделить 2 способа задания игры.
1 так называемая позиционная форма. При этом определяются:
· порядок ходов
· альтернативы (возможные ходы), доступные каждому из игроков на момент наступления его хода
· информация, которой владеет каждый из игроков на момент очередного хода
· выигрыши (для каждого игрока) как функции от выбранных ходов
· вероятностные распределения на множестве возможных состояний внешней среды
2. нормальная или стратегическая форма. Каждый участник (игрок) k, где 
, характеризуется наличием индивидуальной системы целевых установок и множеством стратегий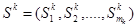 
, т.е. возможных вариантов действий в игре.
Ранее упоминалось о таком понятии, как «антагонистическая игра». Примером такой игры может служить игра «Орлянка». Дадим определение антагонистической игре.
Антагонистическая игра - игра, в которой участвуют два игрока (обычно обозначаемые I и II) с противоположными интересами. Для антагонистической игры характерно, что выигрыш одного игрока равен проигрышу другого и наоборот, поэтому совместные действия игроков, их переговоры и соглашения лишены смысла.. Определяются антагонистические игры заданием множеств стратегий игроков и выигрышей игрока I в каждой ситуации, состоящей в выборе игроками своих стратегий. Таким образом, формально антагонистическая игра есть тройка ‹ А, В, Н›, в которой А и В - множества стратегий игроков, а Н (а, b) - вещественная функция (функция выигрыша) от пар (а, b), где а A, b В. Игрок I, выбирая а, стремится максимизировать Н (а, b),а игрок II, выбирая b, - минимизировать Н (а, b).
Пример 2:
Рассмотрим игру G (4х5) в матричной форме.
| 
| 
| 
| 
| |
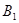
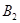
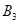
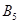
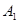
| 3 | 4 | 5 | 2 | 3 |
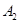
| 1 | 8 | 4 | 3 | 4 |
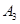
| 10 | 3 | 1 | 7 | 6 |
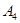
| 4 | 5 | 3 | 4 | 8 |
Очевидно надо выбирать ту стратегию, при которой выигрыш максимален. (Это так называемый принцип минимакса. О нём чуть позже). В правом добавочном столбце запишем минимальное значение выигрыша в каждой строке; обозначим его для i-ой строки 
.
|
| 
| 
|
| 
| 
| |
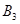
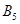
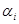
| 3 | 4 | 5 | 2 | 3 | 2 |
|
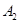
| 1 | 8 | 4 | 3 | 4 | 1 |
|
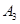
| 10 | 3 | 1 | 7 | 6 | 1 |
| 4 | 5 | 3 | 4 | 8 | 3 |
| 10 | 8 | 5 | 7 | 8 |
Из всех значений выделено наибольшее (3). Ему соответствует величина 
- гарантированный выигрыш, который называется нижней ценой игры. Исходя из принципа осторожности, надо выбрать стратегию 
, а противник должен выбрать стратегию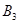 
. Такая стратегия называется «минимаксной». Выше было упомянуто о принципе минимакса. Рассмотрим далее соответствующую терему.
Теорема о минимаксе.
Можно доказать, что для любой функции F(x,y) определённой на произвольном декартовом произведении X × Y имеет место неравенство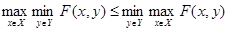 
. Отсюда следует, что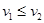 
Запишем 2 утверждения:
Утверждение 1. Точка 0 ( в m-мерном пространстве) содержится в выпуклой оболочке m+n точек
и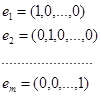 
Утверждение 2. Существуют числа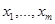 
удовлетворяющие условиям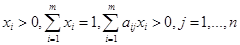 
Доказательство: Пусть А – матричная игра. Имеет место либо утверждение 1, либо утверждение 2. Если верно утверждение 1 то 0 является выпуклой линейной комбинацией m+n векторов. Поэтому существуют такие
что 
Если бы все числа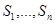 
были бы равны нулю, то 0 оказывался бы выпуклой линейной комбинацией m единичных векторов 
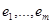, что невозможно, т.к. они линейно независимы. Следовательно, по крайней мере одно из чисел 
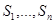положительно и
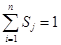
тогда можно положить
и получится 
для всех i
Значит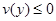 
и 
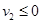
Предположим, что верно утверждение 2. Тогда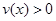 
, так что 
. Следовательно, неравенство 
не имеет смысла. Предположим, что игра А изменена на игру 
, где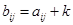 
. Для любых х и y 
, поэтому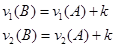 
. Так как неравенство 
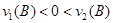не имеет смысла, то неравенство 
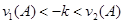также не выполняется. Но k произвольно. Значит неравенство 
невозможно. Т.к. 
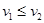то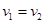 
. Что и требовалось доказать.
Принцип минимакса.
Рассмотрим игру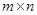 
с платежной матрицей 
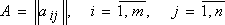Следует определить наилучшую стратегию игрока I среди стратегий 
, 
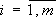и игрока II среди стратегий 
, 
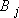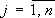. Определение наилучших стратегий игроков основано на принципе, который предполагает, что противники, участвующие в игре, одинаково разумны и каждый из них делает все для того, чтобы добиться своей цели. Найдем наилучшую стратегию игрока I. Допустим, что он выбрал i-ю стратегию (i –ю строку матрицы (1)). Тогда он получит меньше, чем 
– наименьшее число в этой строке. Причем это будет в том случае, если игрок II каким-то образом раскроет стратегию игрока I. Из сказанного следует, что I игрок, если он не желает рисковать, т.е. играть не оптимально, должен действовать следующим образом – определить наименьшие элементы всех строк и выбрать ту из них, в которой это число наибольшее. В этом случае он гарантирует себе выигрыш равный наибольшему из меньших чисел всех строк. Этот выигрыш равен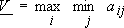 
Число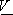 
это “низкий выигрыш” игрока I и его называют нижним значением или нижней ценой игры. Как же рассуждает второй игрок? “Если я выберу j-ую стратегию (j-ый столбец), то самый лучший выигрыш у игрока I будет 
наибольшее число этого столбца. Чтобы рисковать, я должен выбрать столбец, в котором это число наименьшее. В результате I игрок не сможет получить больше, чем 
Число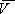 
представляет собой ”верхний выигрыш” игрока I и называется верхним значение или верхней ценой игры. Можно показать, что для всякой матричной игры выполняется условие 
. Если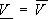 
, то такие игры называются играми с седловой точкой. Из неравенства следует, что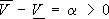 
. Это фактически означает, игрок I мог бы рассчитывать на выигрыш 
.
Матричные игры
В этом параграфе будет рассказано о принципе максимина, рациональном представлении матрицы игры, о решении игры при помощи фиктивного разыгрывания.
| н/ч | ч | |
| н/ч | 1 | -1 |
| ч | -1 | 1 |
Начнём непосредственно с матричных игр. Тройка 
(где x и y – множества, H – функция от двух переменных 
) называется антагонистической игрой. Процесс разыгрывания конечной антагонистической игры (игра называется конечной, если тройка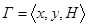 
конечна) состоит в том, что игроки 1 и 2 независимо друг от друга выбирают соответственно некоторые чистые стратегии x и y, в результате чего складывается ситуация (x,y).
Мы знаем, что антагонистическую игру двух участников с нулевой суммой (напомним, что нулевая сумма – это когда выигрыш одного игрока равен проигрышу другого) удобно задавать с помощью, так называемой платёжной матрицы. Каждый элемент такой матрицы 
содержит числовое значение выигрыша игрока 1 (или проигрыша игрока 2) в ситуации, когда первый игрок применяет стратегию i, а второй – стратегию j. Классическим примером антагонистической игры является игра с двумя участниками, которые независимо друг от друга загадывают числа. Предполагается, что если сумма оказывается чётной, то выигрыш равный 1, достаётся первому игроку, а если нечётной, то второму. Если предположить, что загадывание нечётного числа – стратегия первого игрока, а загадывание чётного числа – стратегия второго игрока, то платёжная матрица выглядит следующим образом:
Строки матрицы соответствуют стратегиям игрока 1, столбцы – стратегиям игрока 2, а её элементы – результатам (т.е. выигрышам) первого. Если взять элементы матрицы с обратным знаком, то это будут выигрыши второго игрока. Здесь надо отметить, что вопрос о выборе стратегии является основным в теории игр. Для примера проанализируем произвольную игру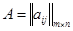 
. При выборе игроком 1 стратегии i, его выигрыш в независимости от игрока 2 составит 
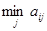. Стратегия I произвольно, поэтому главная цель игрока 1 максимизировать величину полученного выигрыша, т.е. получить 
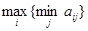. Такой принцип получил название принципа максимина. Напомним, что максимин – это выигрыш максимальный из минимальных. Надо также отметить, что принцип максимина обеспечивает игрокам гарантированный «выигрыш» при любых стратегиях противников.
|
|
|
