 |
Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
|
|
|
|
Построение математической модели
Процесс построения математической модели для решения поставленной задачи можно начать с ответов на три следующие вопроса:
1. Для определения, каких величин должна быть построена модель?
2. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, для моделируемой системы?
3. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?
Отвечая на поставленные вопросы, сформулируем суть проблемы. Фирме требуется определить объемы производства (в тоннах) каждой из красок, который максимизирует доход (в тысячах долларов) от реализации продукции, с учетом ограничений на спрос и расход исходных продуктов.
Введем переменные: так как нужно определить объемы производства каждого вида краски, то переменными в модели являются
· xE - суточный объем производства краски Е (в тоннах)
· xI - суточный объем производства краски I (в тоннах).
Так как стоимость 1 т краски Е равна 3 тыс. долл., суточный доход от ее продажи составит 3 xE тыс. долл. Аналогично доход от реализации xI тонн краски I составит 2 xI тыс. долл. в сутки. При допущении независимости объемов сбыта каждой из красок можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения xЕ и xI, максимизирующие величину общего дохода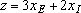 
Ограничения: При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов и спрос на изготовляемые краски. Ограничение на расход исходных продуктов можно записать следующим образом:
Это приводит к следующим двум ограничениям: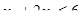 
(для А) 
(для В) Ограничения на величину спроса красок имеют вид
|
|
|
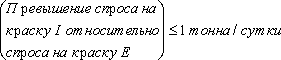
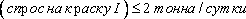
Эти ограничения имеют вид: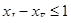 
(соотношение величин спроса на краску I и краску Е), 
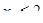(максимальная величина спроса на краску I). Переменные xI и xE не могут принимать отрицательных значений: 
(объем производства краски I),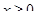 
(объем производства краски Е). Итак, математическую модель можно записать следующим образом. Определить суточные объемы производства (xI и xE) краски I и краски Е (в тоннах), при которых достигается 
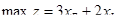(целевая функция) при ограничениях:
Что определяет линейный характер построенной модели? С формальных позиций данная модель является линейной потому, что все входящие в нее функции (ограничения и целевая функция) линейны. Линейность предполагает наличие двух свойств - пропорциональности и аддитивности.
1 Пропорциональность означает, что вклад каждой переменной хЕ и хI в целевую функцию прямо пропорционален этим переменным.
2 Аддитивность заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных. Однако если фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.
Задача о пищевом рационе.
Пусть имеется 4 вида продуктов: 
. Стоимость единицы каждого продукта 
. Согласно этим условиям, требуется составить пищевой рацион, в котором должны содержаться белки, в количестве не менее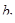 
единиц, углеводов – не менее 
единиц, жиров – не менее 
единиц.
Составим таблицу.
| продукт | элементы | продукт | элементы | ||||
| Белки | углеводы | Жиры | Белки | углеводы | Жиры | ||
| 
|
| 
| 
|
| 
| 
|
| 
| 
| 
|
|
|
| 
|
(
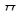
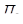
) – какие то определённые числа. Первый индекс указывает номер продукта, второй – номер элемента (белки, жиры углеводы). Требуется составить пищевой рацион таким образом, чтобы условия по белкам, жирам и углеводам были выполнены. Математическая модель будет выглядеть следующим образом: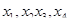 
- количества продукции 
входящих в рацион. Показатель эффективности L – стоимость рациона (эту величину требуется минимизировать). Запишем линейную зависимость 
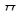. Учитывая, что в одной единице продукта содержится единиц белка, в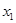 
единицах -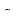 
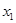единиц белка, в 
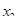единицах продукта 
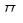содержится 
единиц белка и т.д. получим три неравенства: 
эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения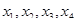 
. Таким образом задача сводится к следующей: найти такие неотрицательные значения переменных 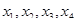, чтобы они удовлетворяли ограничениям – неравенствам и одновременно обращали в минимум линейную функцию этих переменных: 
|
|
|
|
|
|
