 |
Теорема о принципе максимина.
|
|
|
|
Для 
с 
(где 
- множества чистых стратегий игроков, (х, у) – ситуация игры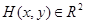 
- функции полезности игроков, заданные на множестве ситуаций 
игры аналитически 
) общего вида
.
Доказательство.
Для
Для игры, заданной матрицей выигрышей 
можно записать следующее равенство 
.
Скажем ещё несколько слов о матричных играх. Для матричных игр доказано, что любая из них имеет решение, и оно может быть легко найдено путем сведения игры к задаче линейного программирования.
Матричная игра игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.
Первый игрок имеет m страте6гий i = 1,2,...m, второй имеет n стратегий j=1,2,...n. Каждой паре стратегий (i, j) поставлено в соответствии число a 
, выражающее выигрыш игрока 1 за счет игрока 2, если первый игрок примет свою i-ю стратегию, а 2-ю j-ю стратегию.
Каждый из игроков делает один ход: игрок 1 выбирает свою i-ю стратегию (i= 
), 2- свою j-ю стратегию (j= 
) после чего игрок 1 получает выигрыш a за счет игрока 2 (если a 
<0, то это значит, что игрок 1 платит второму сумму 
a 
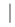). На этом игра заканчивается.
Каждая стратегия игрока i= 
; j= 
часто называется чистой стратегией.
Если рассмотреть матрицу
то проведение каждой партии матричной игры с матрицей А сводится к выбору игроком 1 i- строки, а игроком 2 j-го столбца и получения игроком 1 (за счет игрока 2) выигрыша a .
Главным в исследовании игр является понятие оптимальных стратегий игроков. В это понятие вкладывается следующий смысл: обеспечивается наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока. Исходя из этих позиций, игрок 1 исследует матрицу выигрышей А следующим образом: для каждого значения i (i= ) определяется минимальное значение выигрыша в зависимости от применяемых стратегий игрока 2
|
|
|
min a 
(i= 
)
j
т.е определяется минимальный выигрыш для игрока 1 при условии, что он примет свою i-ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i=i 
, при которой этот минимальный выигрыш будет максимальным, т.е. находится
max min a = a 
= 
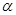(1)
Определение: Число 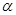, определенное по формуле (1) называется чистой нижнейценойигры показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2.
Игрок 2 при оптимальном своем поведении должен стремиться по возможности за счет своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскивается
max a
i
т.е. определяется max выигрыш игрока 1, при условии, что игрок 2 применит свою j-ю чистую стратегию, затем игрок 2 отыскивает свою j=j 
стратегию, при которой игрок 1 получит min выигрыш, т.е. находит
min max a =a 
= 
(2)
j i
Определение. Число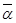 
, определяемое по формуле (2), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счет своих стратегий может себе гарантировать игрок 1.
Другими словами, применяя свои чистые стратегии, игрок 1 может обеспечить себе выигрыш не меньше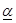 
, а игрок 2 за счет применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем .
Переходя к рациональному представлению матрицы игры, отметим, что стратегии двух игроков сводятся в таблицу, а непосредственно само представление упрощает поиск решения матричных игр.
ПРИМЕР 3: Провести SP-разбиение матрицы игры (Н)
| X1 | 2 | 3 | 4 | 5 |
| X2 | 1 | 4 | 0 | 5 |
| X3 | 1 | 0 | 6 | 7 |
| X4 | 1 | 2 | 3 | 4 |
| Y1 | Y2 | Y3 | Y4 |
| 
| 
| 
| 
| 
|
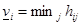
| 2 | 3 | 4 | 5 | 2 |
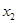
| 1 | 4 | 0 | 5 | 0 |
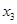
| 1 | 0 | 6 | 7 | 0 |
| 1 | 2 | 3 | 4 | 1 |
| 2 | 4 | 6 | 7 | 
|
Решение: вычисляем верхнюю и нижнюю цену игры
|
|
|
Исходная игра имеет SP 
(x1,y1) в чистых стратегиях. Существование SP в чистых стратегиях матричной игры с полной информацией позволяет провести SP-разбиение (Н) исходной игры:
.
Формирование SP- разбиения матричной игры с SP по существу и является рациональным представлением исходной матрицы (Н) игры. Значит, понятие рациональности представления матрицы игры преследует цель сформулировать методы рационального преобразования платёжной матрицы с целью вычисления цены игры v или упрощения построения подыгры-решения.
Далее рассмотрим такое понятие, как решение, при помощи фиктивного разыгрывания. Есть 2 игрока, которые без теории игр, хотят сделать игру несколько раз, причём каждый из них склонен к статистике и оценивает стратегию своего противника. При каждом разыгрывании противоборствующие стороны стремятся максимизировать свой ожидаемый выигрыш против наблюдаемого вероятностного распределения противника: если игрок 2 использует j-ю стратегию 
раз, то игрок 1 выберет i-ю стратегию, чтобы максимизировать 
. Аналогично, если игрок 1 использует i-ю стратегию 
раз, то игрок 2 выберет j-ю стратегию, чтобы минимизировать 
. Условно эмпирические распределения сходятся к оптимальным стратегиям. Точнее, пусть 
- число использований первым игроком i-ой стратегии в течение первых N розыгрышей. Пусть 
, то тогда 
является смешанной стратегией. Здесь справедливо утверждение о том, что предел любой сходящейся подпоследовательности является оптимальной стратегией, т.е. если 
и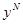 
полученные стратегии игроков 1 и 2, то выполняется равенство 
. Такой метод полезен в случае игры с большим числом стратегий.
Опишем некоторые свойства решений матричных игр. Пусть G(X,Y,A) – игра двух лиц с нулевой суммой, в которой игрок 1 выбирает стратегию 
, а игрок 2 -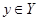 
, после чего игрок 1 получает выигрыш A=A(x,y) за счёт игрока 2.
Свойство 1: Если чистая стратегия одного из игроков содержится в спектре (спектр – множество чистых стратегий, вероятность которых положительна) некоторой его оптимальной стратегии, то выигрыш этого игрока в ситуации, образованной данной стратегией и любой оптимальной стратегией другого игрока, равен значению конечной антагонистической игры.
|
|
|
Свойство 2: Ни одна доминируемая чистая стратегия игрока не содержится в спектре его оптимальной стратегии.
Свойство 3: Если 
– конечная антагонистическая игра, а 
, подыгра игры G причём 
- чистая стратегия игрока 1 в игре G, доминируемая над некоторой стратегией 
, спектр которой не содержит 
. Тогда всякое решение 
игры 
является решением игры G.
Свойство 4: Тройка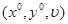 
является решением игры <=>, когда 
является решением игры 
, где а – любое вещественное число, к>0
|
|
|
