Математический аппарат теории игр и его применение к решению прикладных задач

Транспортная задача. Подобная задача возникает в своем простейшем варианте, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителю. Поэтому здесь естественно возникает задача о наиболее рациональном прикреплении транспорта, правильном направлении перевозок груза, при котором полностью удовлетворяются потребности при минимальных затратах на транспортировку. Итак, задача формулируется следующим образом.

Имеется m пунктов производства с объемами производства в единицу времени а _i, i =  и n пунктов потребления b_i, i = , естественно, что потребление не должно превышать возможностей производства a_i   b_i, затраты на перевозку единицы продукции из i -го пункта производства в j -й пункт потребления составляют С _{i j}, а количество перевезенного продукта x_{i j}.

Требуется составить такой план перевозок, при котором суммарные затраты на них были бы минимальны min C_ij x _ij при условиях, что в каждый пункт потребления завозится требуемое количество продукта x_{i j}  b_j, j = , из каждого пункта производства вывозится не более произведенного количества продукта x_{i j}  a _i, =  и перевозимый объем продукта не может быть отрицательным x_ij   0, i = , j = .

Рассмотрим далее транспортную задачу в частной постановке.

На двух станциях отправления  и  сосредоточено соответственно  и  единиц некоторого однородного груза. Этот груз следует доставить в три пункта назначения , , , причём в каждый из них должно быть завезено соответственно , ,  единиц этого груза. Стоимость перевозки единицы груза из пункта  в пункт  (равную ), считаем заданной. Все данные полезно представить в виде таблицы 2.2.

 

Таблица 2.2

Пункты назначения Пункты отправления	Пункты назначения			Запасы груза
Потребность в грузе

 

Естественно считать, что общий запас грузов на станциях отправления равен суммарной потребности в этом грузе всех станций назначения. Следовательно

 (1)

 

Требуется составить такой план перевозок, при котором их общая стоимость была бы наименьшей.

Обозначим через  количество единиц груза, предназначенного к отправке из пункта  в пункт . Тогда количество груза, который планируется к доставке в пункт  из пунктов  и  составит

 

.

 

Но так как потребность в грузе в пункте  равна , то должно выполняться равенство .

Аналогичные рассуждения приводят к равенствам

 

, .

 

С другой стороны, общее количество груза, отправленного со станции , выражается суммой , которая, очевидно, обязана совпадать с запасом груза , сосредоточенным на этой станции, т.е.

 

.

 

Подобно этому .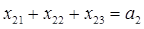

Полученные соотношения легче запомнить, если все величины свести в таблицу 2 (матрицу перевозок). Тогда легко проверить, что сумма всех , расположенных в -ой строке, равна запасу  в пункте назначения . Сумма же всех 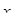 из столбца  равна потребности  пункта назначения .

Таблица 2.3

Пункты назначения Пункты отправления	Пункты назначения			Запасы груза
Потребности

 

Из условий задачи с очевидностью вытекает, что общая стоимость  всех перевозок

 

 

Таким образом, математическая формулировка транспортной задачи (по критерию стоимости перевозок) такова.

Задана система

 

 (2)

 

пяти линейных алгебраических уравнений с шестью переменными и линейная целевая функция

 

(3)

Требуется среди всех неотрицательных решений  системы (2) выбрать такое, при котором целевая функция  минимизируется (достигает наименьшего значения).

Необходимо отметить, что при решении транспортной задачи следует учитывать важное соотношение

 

 (4)

 

вытекающего из самого условия задачи.

Впрочем, возможны и иные постановки транспортной задачи, когда условие (1а) не выполнено.

Задача о выборе производственной программы. Эта задача была одной из первых практических задач линейного программирования, решенная в 1939 году известным русским математиком Л.В.Канторовичем.

На m предприятиях нужно произвести n продуктов в заданном ассортименте l₁, l₂,..., l_n. Если x _ij, i = , j =  – рабочее время i -го предприятия, отводимое под j -й продукт, а_ij – производительность i -го предприятия в единицу времени по выпуску j -го продукта, то задача о выборе производственной программы для случая, когда продукция дефицитна, производственные мощности ограничены и должны использоваться максимально полно, ставится следующим образом.

Требуется составить программу работы предприятий – указать время х _{i j}, отведенное на производство каждого вида продукции на данном предприятии таким образом, чтобы получить максимальный суммарный объем продукции в заданном ассортименте в единицу времени, т.е. необходимо найти x_{i j} из условий, что время не может быть отрицательным x_ij > 0, сумма всех временных долей не превосходит полного времени работы предприятия x_{i j}  1, количество ассортиментных наборов продуктов максимально.

Задача об использовании сырья. Предположим, что изготовление продукции двух видов  и  требует использования четырех видов сырья , , , . Запасы сырья каждого вида ограничены и составляют соответственно , , ,  условных единиц. Количество единиц сырья, необходимое для изготовления единицы каждого из видов продукции, известно и задаётся таблицей 2.4.

Таблица 2.4

Виды сырья	Запасы сырья	Виды продукции
Доход

 

В этой экономической ситуации 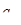 означает количество единиц сырья вида , необходимое для изготовления продукции вида 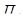. В последней строке таблицы указан доход, получаемый предприятием от реализации одной единицы каждого вида продукции.

Нужно определить такой план выпуска продукции видов  и , при котором доход предприятия от реализации всей продукции оказался бы максимальным.

Математическую форму поставленной задачи изучим на следующем числовом примере (см. таблицу 2.5).

Таблица 2.5

Виды сырья	Запасы сырья	Виды продукции
	19	2	3
	13	2	1
	15	0	3
	18	3	0
Доход		7	5

 

Допустим, что предприятие выпускает 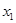 единиц продукции вида  и  единиц продукции вида . Для этого потребуется  единиц сырья  (на основании таблицы 2.5). Так как в наличии имеется всего 19 единиц сырья , то должно выполняться неравенство . Неравенство, а не точное равенство появляется в связи с тем, что максимальный доход может быть достигнут предприятием и в том случае, когда запасы сырья вида  используются не полностью.

Аналогичные рассуждения, проведённые для остальных видов сырья, позволяют записать следующие неравенства:

(сырьё )

(сырьё )

(сырьё ).

При этих условиях доход , получаемый предприятием, составит .

Таким образом, математически рассматриваемую экономическую ситуацию можно сформулировать так.

Дана система

 

четырёх линейных неравенств и линейная целевая функция

 

.

 

Требуется среди неотрицательных решений системы (4) выбрать такое, при котором целевая функция  принимает наибольшее значение (максимизировать).

Рассмотрим на примере ещё несколько игр.

Игра Морро. Игроки показывают одновременно 1 или 2 пальца и в тоже время называют число. Если число, названное одним игроком, совпадает с общим числом пальцев, то игрок получит от своего противника выигрыш, равный этому числу. Если оба угадают верно, то чистый платёж будет равен нулю.

	0	2	-3	0
	-2	0	0	3
	3	0	0	-4
	0	-3	4	0

Оборона города («Игра полковника Блотто»)

Полковник Блотто имеет m полков, а его противник – n полков. Противник защищает 2 позиции. Позиция будет защищена полковником, если на ней наступающие полки окажутся в численном превосходстве. Противоборствующим сторонам тре6уется распределить полки между двумя позициями. Если игрок 1 (полковник) имеет на позиции больше полков, то выигрыш равен числу полков противника плюс один (занимаемая позиция равносильна захвату одного полка). Если у противника (игрока 2) больше полков на позиции, то игрок 1 таким образом теряет свои полки на этой позиции и ещё единицу. Если обе стороны имеют одинаковое количество полков на позиции, то имеет место ничья. Посмотрим на стратегии игроков.

Игрок 1 имеет следующие стратегии:

 - послать все полки на первую позицию

 - послать  полков на первую позицию, а  полков – на вторую позицию и т.д.

 - послать все полки на вторую позицию

Игрок 2 имеет такие стратегии:

- послать все полки на первую позицию

 - послать  полков на первую позицию, а  полков – на вторую позицию и т.д.

 - послать все полки на вторую позицию

Пусть m=4, n=3. Тогда рассмотрев всевозможные ситуации, получим матрицу выигрышей, для этой игры

 

Игрок 1 Игрок 2
	4	2	1	0
	1	3	0	-1
	-2	2	2	-2
	-1	0	3	1
	0	1	2	4

 

Основная задача линейного программирования.

Любую задачу линейного программирования можно свести к ОЗЛП (основной задаче линейного программирования). Основной принцип данной задачи таков: найти такие неотрицательные значения переменных , которые удовлетворяли условиям – равенствам

 

 

и обращали бы в максимум линейную функцию этих переменных: . Если функцию L требуется обратить в минимум, то для этого нужно изменить знак этой функции (т.е. максимизировать не L, а ). Рассмотрим конкретный пример, объясняющий эту позицию.

Пример. Пусть требуется найти неотрицательные значения переменных , удовлетворяющих ограничениям – неравенствам и обращающие в максимум линейную функцию . Приведём условия в фигурной скобке к стандартному виду. Получим (1). А теперь обозначим левые части неравенств через y1 и y2 => (2). Из условий (1) и (2) следует что переменные y1 и y2 тоже должны быть неотрицательными.

Выводы

 

1 Представлены основные понятия теории игр и исследования операций.

2 Приведены примеры игр в чистой и смешанной стратегиях (задача Борьба двух предприятий за рынок продукции региона»).

3 Представлена основная теорема Теории игр (с доказательством) и использован принцип сведения теоретико-игровой модели к ЗЛП (задаче линейного программирования)

4 В работе приведена серия задач, связанных с теорией игр и исследованием операций (в частности – основная задача линейного программирования).

5 Раскрыто современное понятие «Принятие решений» на основе математических методов и моделей Теории игр

ЛИТЕРАТУРА

1. Борисова С.П., Власова И.А., Коваленко А.Г. Теория игр и исследование операций – Издательство «Самарский университет», 2006.

2. Берж Л. Общая теория игр нескольких лиц – М.: ГИФМЛ, 1961. 327.стр.

3. Барсов А.С. Линейное программирование в технико-экономических задачах. М.: Наука, 1964. – 278 с.

4. Воробьёв Н.Н. Матричные игры – М.: Физматгиз, 1961.

5. Власов Д.А., Монахов Н.В., Монахов В.М. Математические модели и методы внутримодельных исследований – Издательство «Альфа», 2007.

6. Вентцель Е.С. Исследование операций. Задачи, принципы, методология – М.: Дрофа, 2006. 208 страниц.

7. Гасс С. Линейное программирование (методы и приложения) – М., 1961.

8. Гамецкий А.Ф., Слободенюк В.А., Спиридонова Г.В. Теория игр, исследование операций – Издательство КГУ, 1987.

9. Громенко Г.Н. Теория игр – М.: Издательство МГОУ, 2005. 198 стр.

10. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр – М.: Наука, 1989. 310 стр.

12. Давыдов Э.Г. Исследование операций: учебное пособие – М., 1990.

13. Зайченко Ю.П. Исследование операций – Киев, 1979. 278 стр.

14. Краснов М.Л., Киселёв А.И. Высшая математика, том 5 – М.: Издательство ЛКИ, 2007. 300 стр.

15. Конюховский П.В. Математические методы исследования операций в экономике - СПб.: Издательство СПбГУ. 394 стр.

16. Карлин С. Математические методы в теории игр, программировании и экономике – М., 1964. 400 стр.

17. Льюис Р.Д., Райфа Г. Игры и решения. – М.: ИЛ, 1961 285 стр.

18. Лагунов В.Н. Игры преследования и введение в теорию игр. Т., 1993

19. Мак-Кинси Дж. Введение в теорию игр. – М.: Физматгиз, 1960.

20. Малыхин В.И.. Статкус А.В. Теория принятия решений. МИУ, М., 1989. 382 стр.

21. Мулен Э Теория игр с примерами из математической экономики - М.: Мир 1985.

22. Нейман Дж. Фон, Моргенштерн О. Теория игр и экономическое поведение – М.: Издательство «Наука», 2007. 420 стр.

23. Нестеров Е.П. Транспортные задачи линейного программирования – М.: Транспорт 1971. 216 стр.

24. Оуэн Г. Теория игр - М.: Издательство ЛКИ, 2007. 232 стр.

25. Петросян Л.А. Теория игр – М.: Издательство «Высшая школа», 1998.

26. Протасов И.Д. Теория игр и исследование операций – М.: Издательство «Гелиос» АРВ, 2006. 368 страниц.

27. Парфёнов Г.Н. Принципы теории игр – Издательство СПбГУ, 2001.

28. Секацкий В.В., Худякова Г.И. Элементы теории матричных игр в курсе математики.// Ярославский педагогический вестник. 2000, №1(23).

29. Терехов Л.Л. Применение математических методов в экономике – М.: Статистика, 1968. 188 стр.

30. Таха Х. Введение в исследование операций – М.: издательство «Вильямс», 2001.

31. Фатхутдинов Р.А. Управленческие решения – М.: нфра 2007.

32. Хорн Р., Джонсон Ч. Матричный анализ – М.: Мир, 1989. 427 стр.

33. Хазанова Л.Э. Математические методы в экономике – М.: издательство БЕК, 2002. 144 стр.

34. Шикин Е.В. От игр к играм – М.: УРСС, 1997. 149 стр.

35. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование. Теория, методы, приложения – М.: «Наука», 1969. 364 стр.

36. Яновская Е.Б. Антагонистические игры // Проблемы кибернетики. – М.: Наука, 1978. С. 221 – 246.

Предыдущая12345678Следующая

Поделиться:

Воспользуйтесь поиском по сайту: