 |
Способы создания и оценки репрезентативности выборки
|
|
|
|
С точки зрения статистического подхода репрезентативность выборки обеспечивается выполнением следующих условий: а) каждый из объектов генеральной совокупности должен иметь одинаковую вероятность быть представленным в выборке; б) отбор производится из однородных совокупностей; в) число объектов в выборке должно быть достаточно большим; г) выборка и генеральная совокупность должны быть по возможности статистически однородны.
Создание простой вероятностной выборки может осуществляться методом рандомизации – процедурой случайного отбора.При этом методе характеристики испытуемых игнорируются, их включение в выборку имеет одинаковую вероятность и является непредвзятым. Это значит, что любой испытуемый имеет равные шансы попасть в выборку. Процедура построения простой случайной выборки включает в себя следующие шаги: а) необходимо получить полный список членов генеральной совокупности и пронумеровать этот список; б) определить предполагаемый объем выборки, то есть ожидаемое число испытуемых; в) извлечь из таблицы случайных чисел столько чисел, сколько требуется выборочных единиц (например, если в выборке должно оказаться 100 человек, из таблицы берут 100 случайных чисел, которые могут генерироваться компьютерной программой). Упрощенным вариантом рандомизации является механический отбор испытуемых на основе списка генеральной совокупности через определённый интервал (К), который определяется случайно.
Несмотря на свою простоту, этот метод имеет существенные ограничения:
- значительно увеличивает трудозатраты и стоимость сбора данных, если генеральная совокупность является численно большой или распределенной по большой географической территории (это характерно при создании ПДМ, рассчитанных на широкие слои населения);
|
|
|
- результаты применения простой случайной выборки часто характеризуются низкой точностью и большой стандартной ошибкой.
В случае неоднородной генеральной совокупности, прежде чем формировать выборку, рекомендуется разделить эту совокупность на однородные части. Они могут формироваться на основе того или иного признака: административно-территориальные единицы (например, районы города), социально-демографические характеристики (пол, возраст, социальный статус) или организационная принадлежность испытуемых (образовательные учреждения) и т.д. Такая выборка называется районированной (стратифицированной). Далее из каждой однородной части отбор в выборку осуществляется случайным образом. Например, для оценки методики изучения межличностной идентичности в группе и подгруппах и методики изучения микрогрупповой и групповой идентичности (применительно к учебным группам подростково-юношеского возраста) были выбраны шесть средних общеобразовательных школ в трех районах и два вуза г. Ростова-на-Дону. Далее методом случайного отбора в выборку были включены по шесть групп 10-х и 11-х классов школ и шесть студенческих групп 2 курса вузов (всего 18 групп).Общая численность испытуемых составила 413 человек.
Ещё одним вариантом рандомизации является создание серийной (гнездовой или кластерной) выборки. Здесьединицами случайного отбора выступают не сами объекты, а группы (кластеры или гнёзда). Объекты внутри групп обследуются сплошным образом.
Создание невероятностной выборки, что широко практикуется при оценке психодиагностических методик и составлении нормативов, осуществляется не по принципу случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д. Выделяют несколько способов формирования такой выборки:
|
|
|
1) Метод квотирования. Изначально выделяется некоторое количество групп объектов (например, мужчины и женщины в возрасте 18-25 лет, 26-35 лет и 36-55 лет. Для каждой группы задается количество испытуемых, которые должны быть обследованы с помощью данной методики. Количество испытуемых, которые должны попасть в каждую из групп, задается либо пропорционально заранее известной доле группы в генеральной совокупности (например, если генеральная совокупность представлена 5000 человек, из них 2000 женщин и 3000 мужчин, тогда в квотной выборке будет 200 женщин и 300 мужчин), либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно.
2) Метод «снежного кома». Выборка строится следующим образом: у каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования.
3) Метод стихийного отбора.Опрашиваются наиболее доступные респонденты. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – желанием и активностью респондентов.
4) Метод отбора типичных объектов. После районирования (стратификации) из каждой группы отбирается типичный объект, т.е. объект, который по большинству изучаемых в исследовании характеристик приближается к средним показателям.
Репрезентативность выборки измеряется разностью между характеристиками выборочной и генеральной совокупностей. (Чем более выборка и генеральная совокупность являются статистически однородны, тем более выборка репрезентативна.) Однако фактическая величина указанной разности остаётся неизвестной, вследствие чего мерой репрезентативности служит определяемая по правилам математической статистики её вероятная величина или же средняя квадратическая её возможных значений.
При разработке, оценке и стандартизации методики суждение о степени репрезентативностивыносится на основе оценки минимального объема выборк и и соответствия эмпирического распределения нормальному.
Требуемый объем выборки для обеспечения её количественной репрезентативности часто определяется как минимальный объем выборки, необходимый для того, чтобы выборочное среднее значение ( 
) отличалось от истинного среднего значения генеральной совокупности не более, чем на заданную величину. В этом случае минимальный объем выборки может оцениваться посредством определения доверительного интервала для среднего значения по показателям методики:
|
|
|
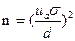, (2)
где n – минимальный объем выборки, ua – значения для стандартных доверительных вероятностей, 
- выборочное стандартное отклонение, d – заданная величина отклонения выборочного среднего значения от генерального среднего.
Например, по методике изучения общительности-замкнутости мы провели пилотажное обследование 50 испытуемых. С помощью «ключа» производим обработку результатов и получаем тестовые показатели по каждому испытуемому. Далее на этой выборке (N=50) проводим расчет:
а) среднего значения: 
, (3)
где 
- тестовый показатель каждого испытуемого, N – количество испытуемых;
б) стандартного (среднеквадратического) отклонения: 
(4).
По результатам выборочного исследования среднее значение составляет 11,25 и стандартное отклонение – 3,47. Задаемся, например, доверительной вероятностью 95% (ua= 1,96 в табл. 1) и отклонением выборочного среднего значения от истинного значения среднего результата не более чем на d = 0,5 и по формуле (1) находим
= 154.
Таким образом, при объеме выборки n = 154 существует 95%-ная вероятность того, что выборочное среднее арифметическое будет отличаться от генерального среднего не более чем на 0,5 баллов.
Таблица 1
Значения ua для стандартных доверительных вероятностей
| a | 1 - a | u a |
| 0,05 | 0,95 | 1,96 |
| 0,01 | 0,99 | 2,58 |
| 0,001 | 0,999 | 3,28 |
В этом случае нам надо провести дополнительное обследование 104 испытуемых и, тем самым, довести объем выборки до 154. Величина минимального объема выборки зависит от заданного уровня доверительной вероятности, величины d и выборочного стандартного отклонения. Чем больше будет доверительная вероятность, меньше величина d или больше стандартное отклонение, тем потребуется большая по численности минимальная выборка.
|
|
|
Нормальное распределение наиболее часто применяют для статистического описания совокупности эмпирических данных, оценки репрезентативности выборки и шкалы (методики), для стандартизации тестовых баллов (на основе перевода в интервальную шкалу). На свойствах нормального распределения основаны статистические критерии проверки гипотез (z-критерий, критерий 
, F-критерий Фишера, t-критерий Стъюдента и др.).
Нормальность распределения оценивается с помощью критерия 
Колмогорова – Смирнова, который считается наиболее состоятельным для определения степени соответствия эмпирического распределения нормальному. Если p >0,1, то делается вывод о приблизительном соответствии данного эмпирического распределения нормальному. В качестве примера можно привести показатели оценки нормальности распределения по шкалам многомерного профессионально-психологического личностного теста.
Сравнение эмпирического распределения с теоретическим нормальным распределением можно также осуществлять посредством оценки таких свойств как асимметрия ( 
) и эксцесс ( 
). Асимметрия и эксцесс нормального распределения равны нулю. Если хотя бы один из этих двух показателей проверяемого эмпирического распределения существенно отклоняется от данного значения, это означает аномальность оцениваемого распределения.
Асимметрия эмпирического распределения определяется по формуле:
, (5)
где 
- среднее арифметическое значение, - стандартное отклонение,
- среднее кубическое ( 
), (6)
С – среднее квадратическое ( 
) (7).
Эксцесс определеяется по формуле:
, (8)
где Q – среднее значение четвертной степени ( 
) (9).
Проверку статистической значимости вычисляемого показателя асимметрии можно провести на основе неравенства Чебышева:
, (10)
где 
- дисперсия эмпирической оценки асимметрии, которая вычисляется следующим образом: 
(11), р – уровень значимости (р= 0,05 или р= 0,01).
Подобным образом оценивается значение эксцесса:
, (12)
где 
- эмпирическая дисперсия оценки эксцесса, которая вычисляется по формуле: 
(13).
Если эмпирическое распределение не соответствует нормальному, то выборка не репрезентативна по качеству и/или количеству. Однако это может свидетельствовать и о том, что данная методика не дает нормального распределения результатов, так как плохо составлен стимульный материал (например, многие тестовые задания не обладают средней диагностической силой).
Понятие стандартности
Стандартность – унификация, приведение к единым нормативам разных частей ПДМ и процедуры ее применения.
|
|
|
Психодиагностические методики с самого начала их разработки задумываются как универсальные, неспецифические, т.е. такие, которые могут использоваться разными специалистами в различных ситуациях. Поэтому ПДМ должна иметь единообразную процедуру проведения, стандартный стимульный материал (утверждения, рисунки и т.д.), стандартный метод обработки и способ интерпретации результатов. Именно это позволяет сравнить выводы, т.е. оценить проявление одного и того же психического параметра в разных ситуациях и у разных людей и, в зависимости от силы проявления диагностируемого параметра, выработать адекватные рекомендации. Стандартность ПДМ и условий ее применения дает возможность сравнивать результаты, полученные разными специалистами при диагностике различных людей. При любом отклонении ПДМ от стандарта, ее результаты невозможно сравнивать с результатами, полученными с помощью оригинала данной методики, использованной на других людях или в другой ситуации.
Однако отсутствие или нарушение стандартности ПДМ не означает, что данной методикой вообще невозможно пользоваться. Нестандартизированную методику можно использовать в научно-исследовательских целях – изучать новые психические явления, выявлять новые факты и накапливать научные результаты, устанавливать причинно-следственные связи и закономерности. Однако такой методикой нельзя пользоваться в психодиагностических целях.
|
|
|
