Точность и ошибки измерения

Психодиагностическая методика рассматривается как обычная шкала для измерений, принятых в естественных науках. Каждая такая шкала характеризуется определённой точностью. Например, метровая линейка для измерения тканей, в которой деления расположены через каждые 5 мм, обладает невысокой точностью, и погрешность измерения лежит в пределах 5 мм. На обычной ученической линейке, на которую нанесены миллиметровые деления, точность значительно выше. Погрешность измерения такой линейкой лежит в пределах 1 мм. Существуют специальные измерительные устройства, которые образуют шкалы с очень маленькой погрешностью измерения. Например, микрометр, точность измерения которого будет очень высока, а погрешность будет лежать в пределах 1 микрона.

Можно ли применить понятие точности и погрешности измерения к ПДМ? В принципе можно. ПДМ принципиально ничем не отличается от обычной измерительной шкалы. Непонятно только другое. С чем можно сравнить точность ПДМ - с точностью микрометра или с точностью портняжного метра? Если для измерения всевозможных размеров имеется большое количество разнообразных измерительных приборов, образующих измерительные шкалы различной точности, то при измерении психических свойств пока существуют только ПДМ, точность которых не с чем сравнить.

В психодиагностической литературе точность измерения обычно рассматривается в контексте разброса (дисперсии) результатов произведенных с помощью методики измерений. В самом широком смысле точность измерения показывает, в какой сте­пени индивидуальные различия в тестовых показателях могут быть отнесены на счет «истинных» различий в изучаемых свойствах, а в какой могут быть приписаны слу­чайным ошибкам. Иначе говоря, надо определиться с тем, какую долю общей дисперсии (общей изменчивости) тестовых показа­телей составляет дисперсия ошибок. Это не «ошибки» в обычном смысле слова, пред­полагающем, что их можно было бы избежать или скорректировать путем усовершен­ствования методологии измерений.

Надо иметь в виду, что факторы, которые применительно к одним задачам можно было бы счесть источниками случайной вариации показателя (т.е. дисперсии ошибок), при решении других задач могут быть отнесены, и не без основания, к причинам его истин­ной дисперсии. Например, если бы нас интересовало измерение колебаний настрое­ния, то происходящие день ото дня изменения в показателях шкалы «радость - уны­ние» были бы релевантны цели данного теста и, следовательно, составляли бы часть истинной дисперсии показателей. С другой стороны, если бы тест предназначался для измерения более устойчивых характеристик личности, те же ежедневные колебания попали бы уже в разряд дисперсии ошибок.

В сущности, любое условие тестирования, которое не имеет отношения к цели теста, представляет собой источник дисперсии ошибок. Поэтому, стремясь к поддер­жанию единых условий тестирования (контролируя общую обстановку, временные ограничения, инструкции испытуемым и другие аналогичные факторы), пользователи тестов способствуют уменьшению дисперсии ошибок и повышению на­дежности тестовых показателей. Но и при оптимальных условиях тестирования ни один тест не является абсолютно надежным инструментом. Поэтому каждый тест сле­дует сопровождать сведениями о его надежности. Сообщаемая мера надежности ха­рактеризует тест только в случае его проведения в стандартных условиях и с людьми, имеющими сходство с теми, кто входил в состав нормативной выборки. Следователь­но, при описании теста нужно точно указывать и характеристики этой выборки, вме­сте с типом измеренной на ней надежности.

Стандартная ошибка измерения вычисляется по следующей формуле:

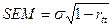, (1)

где - стандартное отклонение показателей теста на выборке испытуемых, - коэффициент надежности.

Например, если стандартные показатели IQ конкретному тесту интеллекта имеют =15 и коэффициент надежности =0,89, то SEM в этом тесте будет составлять .

Эта мера особенно удобна для оценки индивидуальных показателей. Например, тестовый показатель испытуемого А составляет 110. Вследствие разного рода случайных ошибок показатели этого испытуемого могут варьироваться вокруг истинного показателя (110), подчиняясь нормальному распределению. Среднее это­го распределения ста показателей можно принять за «истинный показатель» для дан­ного использования теста, а стандартное отклонение — за соответствующую SEM. Как и любое стандартное отклонение, стандартную ошибку можно интерпретировать в единицах плотности нормального распределения. При нормальном распределении в интервал + попадает приблизительно 68 % всех случаев. Следовательно, имеется примерно 2 шанса против 1 (точнее, 68:32), что IQ испытуемого А по этому тесту будут колебаться в пределах ± 1 SEM или 5 единиц в обе стороны от его истинного IQ. Если его истинный IQ = 110, можно ожидать, что в 2/3 (68 %) случаев показанные им результаты попадут в интервал между 105 и 115.

Несмотря на то что в литературе описаны приёмы определения точности и погрешностей измерения ПДМ, надо сказать, что в подавляющем большинстве описаний той или иной ПДМ нет указаний на точность или погрешность измерений. (Иногда специалисты апеллируют к показателям оценки ретестовой надежности и надежности-согласованности методики как к критериям точности измерения.) Таким образом, определение точности ПДМ и погрешности её измерения скорее пожелание, а не практическая реальность.