Квантильная стандартизация

В некоторых случаях знания степени отклонения индивидуального результа­та от среднегруппового бывают недостаточны. Экспери­ментатору необходимо оценить место, которое занимает испытуемый в популяции по исследуемому параметру, т. е. узнать, какой процент испытуемых выполняет тест хуже или лучше обследованного лица, имеет бо­лее высокие или более низкие оценки и т.п. Ответ на эти вопросы может быть получен на основе распреде­ления накопленных частот.

Квантильная стандартиза­ция – преобразование, связанное с определением места испытуемого в выборке, а точнее с определением процента испытуемых, получивших такой же или более низкий тестовый показатель по сравнению с данным испытуемым.

На рис. 4 по оси абсцисс отложены нормиро­ванные значения тестовых оценок, а по оси ординат — накопленная частота. Кривая накопленной частоты позволяет легко определить место испытуемого в норма­тивной выборке, т.е. перейти от одной шкалы оценок к другой. Исходные оценки выражают результаты тести­рования через задания теста, а преобразованные — че­рез популяцию. Как видно в рис. 4, обе эти шка­лы связаны нелинейным образом. Изменением шкалы по оси ординат кривая может быть превращена в пря­мую линию.

 

Рис. 4. Кривая накопленной частоты

 

Однако на практике используются не точные, а ин­тервальные оценки места испытуемого в популяции. С этой целью ось накопленной частоты разбивается на фиксированное число равных интервалов. Точка на оси накопленной частоты, делящая ось в установленной пропорции, называется квантилем, поэтому этот вид стандартизации называется квантильной стандартиза­цией.

Квантиль – точка на оси накопленной частоты, делящая ось в установленной пропорции. Квантиль — это общее понятие, а квартили, квинти­ли, децили и процентили — его наиболее частные реали­зации. Имеются, например, три квартиля (Q1, Q2, Q3), ко­торые делят выборку на четыре равные части (кварты) таким образом, что 25% испытуемых располагаются ниже Q1, 50% — ниже Q2 и 75% — ниже Q3. Четыре квинтиля делят выборку аналогичным образом на пять, девять децилей — на де­сять, а 99 процентилей — на 100 равных частей.

Номер квантиля используется в качестве новой пре­образованной тестовой оценки. Он показывает относи­тельное положение испытуемого в нормативной выбор­ке. Например, квартальная оценка 3 и процентильная оценка 75 указывают, что более высокую тестовую оценку могут иметь только 25% испытуемых.

 

Глава 8. Надежность и валидность

Понятие и виды надежности

Надежность ПДМ – независимость методики от любых внутренних и внешних, осознаваемых или неосознаваемых, учтенных или неучтенных факторов, которые могут внести погрешность в измерение величины исследуемого параметра. Надежность, наряду с валидностью и стандартностью, обеспечивает достоверность получаемых результатов.

Виды надежности:

1) Ретестовая надежность – относительно устойчивая воспроизводимость (сходство) результатов тестирования по ПДМ в течение определенного периода времени.

Эта устойчивость зависит от случайных колебаний в выполнении заданий от одного сеанса тести­рования к другому, от неконтролируемых условий тестирования, таких как резкие изменения погоды, внезапные шумы и другие отвлекающие факторы, от изменений в состоянии испытуемых (например, болезнь, утомление, эмоциональное напряжение, беспокойство и др.). Ретестовая надеж­ность показывает, в какой степени результаты теста можно распространить на различ­ные случаи его применения. Чем выше надежность, тем менее чувствительны тестовые показатели к случайным изменениям состояния тестируемых и обстановки тестирования.

Существует несколько ограничений оценки ретестовой надежности. Во-первых, этот вид надежности принципиально не может оцениваться относительно методик, предназначенных для диагностики психических характеристик (например, состояний), подверженных изменению в течение короткого периода времени. В этом случае будет иметь место, как правило, низкий показатель надежности, отражающий не столько данное свойство методики, сколько динамичность измеряемого с её помощью психического явления. Следовательно, эта надежность оценивается тогда, когда методика направлена на исследование относительно устойчивого психического свойства, медленно изменяющегося во времени.

Во-вторых, возникает проблема временного интервала между двумя замерами. Интервал между первым и повторным исследованием должен быть не слишком коротким. Иначе испытуемые будут помнить свои ответы на пункты методики (например, в тест-опросниках) в первом обследовании и стараться отвечать таким же образом во втором или, ухватив принцип решения и построив всю цепь рассуждений (например, в тестах интеллекта), в дальнейшем могут воспроизводить правильный ответ. Следовательно, результаты двух предъявлений теста не будут независимыми, и корреляция между ними окажется обманчиво высокой.

В то же время, интервал не должен быть очень длинным, иначе личностное свойство может измениться. Обычно этот интервал составляет от 3-х недель до 3-х месяцев. Его продолжительность зависит от возраста испытуемых и меры вариабельности измеряемой характеристики. Так, при тестировании маленьких детей этот период должен быть еще короче, чем у испытуемых старшего возраста, поскольку в первые годы жизни связанные с возрастным развитием изменения наблюдаются ежемесячно и даже быстрее. Например, для оценки ретестовой надежности методики изучения доверия детей к незнакомым взрослым было проведено повторное тестирование через шесть месяцев. За индекс надежности был принят коэффициент корреляции Пирсона между результатами двух исследований, который оказался равным 0,38 и статистически незначимым. Однако это не свидетельствует о низкой ретестовой надежности методики, так как анализ возрастной динамики доверия детей от пяти к семи годам показал, что оно сильно снижается, а значит, является вариабельной характеристикой в возрастном аспекте. Скорее всего, надо было установить меньший временной интервал между двумя измерениями.

Таким образом, ретестовая надежность применима только к тем тестам, на которые их повторное проведение на одних и тех же испытуемых не оказывает заметного влияния.

2) Надежность параллельных форм – сходство результатов, получаемых с помощью разных форм одной и той же ПДМ (например, форма А и Б EPI – личностного опросника Айзенка).

При разработке взаимозаменяемых форм надо обеспечить их действительную параллельность. Важно, чтобы парал­лельные формы конструировались как независимые тесты, отвечающие, однако, од­ним и тем же требованиям. Такие тесты должны содержать одинаковое число зада­ний, представленных в одной и той же форме и с однотипным содержанием, а также имеющих примерно одинаковую диагностическую силу. Инструкции, формат бланков и др. также должны быть единообразными.

Помимо оценки надежности, наличие параллельных форм желательно и по другим сооб­ражениям: взаимозаменяемые формы полезны при повторных исследованиях, служат средством уменьшения вероятности формирования опыта («натаскивания») при выполнении тестов и преднамеренного искажения ответов.

Надежность взаимозаменяемых форм характеризуется рядом ограничений. Прежде всего, если изучаемые характеристики подвержены значительному влиянию тренировки (например, в некоторых тестах интеллекта), использование параллельных форм ослабит, но не устранит его полностью. Это приведет к снижению корреляции между двумя формами, а значит, к снижению данного вида надежности. Другая проблема связана с возможным изменением сущности теста при повтор­ном его проведении. Например, если в параллельных задачах на мышление применен один и тот же принцип, то большинство испытуемых, однажды найдя реше­ние, и во второй раз применят его. В подобных случаях одной замены содержания заданий явно недостаточно для того, чтобы избежать переноса принципа решения из одной формы теста на другую. Наконец, следует добавить, что для многих тестов взаимозаменяемые формы отсутствуют ввиду практических трудностей со­здания подлинно эквивалентных форм. В силу этих причин часто приходится обра­щаться к другим методам оценки надежности методики.

3) Надежность-согласованность – сходство результатов (ответов, реакций) по разным частям стимульного материала ПДМ.

Этот вид надежности можно определить на основании однократного применения единственной формы теста, пользуясь для этого различными процедурами расщепления теста, как правило, на две равноценные половины или на такое количество, сколько заданий в стимульном материале. Вре­менная устойчивость показателей в такой характеристике надежности не представле­на, поскольку она предполагает только один тестовый замер.

Оценка надежности

1. Ретестовая надежность. Самый простой способ определения этого вида надежности – проведение двух обследований с помощью методики на одной и той же выборке испытуемых через определенный интервал времени. В этом случае коэффициент надежности (г_я) просто равен корреляции между двумя рядами тестовых показателей.

По существу, коэффициент корреляции (г) выражает степень соответствия или связи между двумя множествами показателей. Вычисляемые по реальным данным коэффициенты корреляции попадают между граничными значениями (-1 и +1) и обычно отличаются от нуля, но практически всегда оказываются меньше единицы (по абсолютному значению). Коэффициенты корреляции можно вычислять разными способами, в зависимо­сти от природы данных. Наибольшее распространение получил коэффициент корреля­ции Пирсона.

, (16)

 

где xi и yi – тестовые оценки i испытуемого по двум замерам, и - средние значения, соответственно, по первому и второму замеру на выборке испытуемых, и 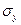- среднеквадратические отклонения по первому и второму замеру на выборке испытуемых, n – количество пар значений.

Этот коэффициент учитывает не только поло­жение индивида в группе, но и степень его отклонения в ту или иную сторону от среднего уровня выборки.

Если коэффициент корреляции между двумя тестовыми замерами составляет от +0,7 до +0,9 (на уров­не р<0,01), то ретестовая надежность считается высокой, а если более + 0,9, то – очень высокой. Чем больше объем выборки, на которой производилась оценка ретестовой надежности, тем о более высокой надежности свидетельствуют одни и те же значения коэффициента корреляции. Например, коэффициент г=0,81, полученный по методике на выборке N=270, свидетельствует о более высокой надежности, чем если бы такое значение корреляции было получено на выборке N=120.

Надо иметь в виду, что значения коэффициентов корреляции при оценке надежности шкал субъективного типа будут снижаться при следующих условиях:

- оценка многомерных методик по сравнению с одномерными тестами;

- использование трех- и пятиальтернативных вариантов ответов по тестовым заданиям, особенно с развернутой формулировкой;

- наличие тестовых заданий, обладающих средней диагностической силой.

Возникает противоречивая ситуация, когда повышение надежности-согласованности сопровождается ухудшением других характеристик методики и наоборот.

В описании процедуры и результатов оценки методики всегда следует указы­вать, в каком интервале времени измерена ретестовая надежность. Поскольку корреляции постепенно снижаются по мере увеличения этого интервала, для любого теста суще­ствует не один, а бесконечное множество ретестовых коэффициентов надежности. Желательно также давать некоторые сведения о событиях, происшедших за время между двумя сеансами тестирования с теми, на ком измерялась надежность теста. Также хорошо было бы знать, какими соображениями руководствовался разработчик при выборе именно этого интерва­ла.

2. Надежность параллельных форм. Одних и тех же испы­туемых тестируют в первый раз с помощью одной формы, а второй раз – посредством другой, эквивалентной формы. Корреляция между показателями, полу­ченными по двум формам теста, представляет его коэффициент надежности. Заме­тим, что такой коэффициент надежности служит мерой как временной устойчивости, так и согласованности ответов на различные выборки заданий (или формы теста). Таким образом, этот коэффициент служит смешанной характеристикой двух типов надежности. Однако поскольку оба ее типа важны для большинства целей тестирова­ния, надежность взаимозаменяемых форм оказывается полезной мерой для оценки многих тестов.

Как и в случае ретестовой надежности, сведения о надежности параллельных форм всегда должны сопровождаться указанием длительности временного интервала между двумя предъявлениями теста, а также характеристикой релевантных событий, происшедших за это время в жизни испытуемых. Если обе формы применяются не­посредственно одна за другой, то полученная корреляция показывает только надежность параллельных форм, но ничего не говорит о надежности как временной устойчивости. Дисперсия ошибок в этом случае обусловлена колебаниями результатов при переходе от одного набора заданий к другому, а не временными флуктуациями показателей.

3. Надежность-согласованность. Этот вид надежности можно определить посредством деления теста либона две равноценные половины, либо на столько частей, сколько содержится в нём заданий, с оценкой связи между частями теста.

3.1. Надежность эквивалентных половин теста. При таком способе каждый испытуемый получает два показателя благодаря разделе­нию теста на две эквивалентные части.

Первая проблема, с которой приходится сталкиваться при применении метода расщепле­ния, связана с тем, как разделить тест, чтобы добиться максимальной эквивалентно­сти его половин. Всякий тест можно членить многими способами. В большинстве тестов первая и вторая половины оказались бы неэквивалентными вследствие разли­чий в характере и уровне трудности заданий, а также в связи с кумулятивными эф­фектами вхождения в работу, утомления и любых других факторов, воздействие которых нарастает от начала к концу теста. Подходящий для большин­ства целей метод состоит в вычислении показателей отдельно по четным и нечетным заданиям теста.

Полученные показатели по двум частям теста коррелируются обычным методом. Однако эта корреляция показывает на­дежность лишь половины теста. Например, если весь тест состоит из 24 заданий, то корреляция вычисляется между двумя множествами показателей, каждый из кото­рых основан только на выполнении 12 заданий. В отличие от надежности этого типа, при расчете ретестовой надежности и надежности параллельных форм, каж­дый показатель основывается на полном наборе заданий теста.

Поэтому применительно к расчетам надежности эквивалентных частей теста используется формула Спирмена – Брауна, предполагающая удвое­ние числа заданий теста:

, (17)

где rhh – коэффициент корреляции эквивалентных половин теста.

При прочих равных условиях, чем больше заданий содержит тест, тем выше его надежность. Вполне оправданно ожидать, что чем обширнее выборка поведения, тем адекватнее и согласованнее получаемые единицы измерения.

Альтернативный метод вычисления надежности эквивалентных половин теста разработан Рюлоном:

, (18)

где 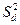- дисперсия разностеймежду показателями каждого испытуемого по обеим половинам теста, - дис­персия показателей по полному тесту.

Любая разность между показателями испытуемого по двум половинам теста от­ражает постороннее влияние или дисперсию ошибок. Дисперсия таких разностей, поделенная на дисперсию показателей по всему тесту, дает долю дисперсии ошибок в этих показателях. Вычитая эту дисперсию ошибок из единицы, мы получаем долю «истинной» дисперсии для установленного применения теста, которая равна его ко­эффициенту надежности.

3.2. Надежность совокупности тестовых заданий. Этот метод оп­ределения надежности, также использующий однократное предъявление единствен­ной формы теста, основан на оценке согласованности ответов по всем заданиям теста. На эту внутреннюю согласованностьвлияют два источника дисперсии ошибок: а) выборочная представленность содержания (как в случае надежности параллельных форм и экви­валентных половин теста); б) неоднородность содержания тестовых заданий. Чем однороднее задания, тем выше внутренняя согласованность. Например, если один тест включает только задания на умножение, а другой — на сложение, вычитание, умножение и деление, то первый тест, вероятно, покажет более высокую внутреннюю согласованность, чем второй. Во втором, более разнородном тесте один испытуемый может лучше справиться с вычитанием, чем с другими арифметическими действия­ми, другой покажет относительно высокий результат в делении, но хуже проявит себя в сложении, вычитании и умножении и т д.

Существует несколько способов оценки этой разновидности надежности-согласованности.

Коэффициент надежности Кьюдера – Ричардсона. Внутренняя согласованность находится по данным однократного проведе­ния единственной формы теста, но вместо использования показателей по двум экви­валентным половинам теста эта методика опирается на результаты выполнения каж­дого задания. Из различных формул шире других применяется так называемая формула КR-20:

, (19)

где rtt – коэффициент надежности полного теста, п – число заданий в тесте,

– стандартное отклонение суммарных показателей теста, p и q – доля испытуемых, соответственно справившихся (р) и не справившихся (q) с каждым заданием.

Чтобы вычислить , нужно для каждого задания найти произведение p х q, а затем сло­жить эти произведения по всем заданиям.

Коэффициент альфа Кронбаха. Формула Кьюдера – Ричардсона применима лишь к тем тестам, в которых выпол­нение заданий оценивается по принципу «А – не-А» (альтернативные признаки), т.е. «да» или «нет», «верно» или «не верно». В некоторых тестах, однако, практикуется более дифференциро­ванная форма представления результатов заданий. Например, в личност­ном опроснике испытуемый может получить различные числовые показатели по любому конкретному пункту опросника в зависимости от того, на какой из готовых категорий ответов он остановил свой выбор: например, «да», «пожалуй, да», «нечто среднее», «пожалуй, нет», «нет». Для таких тестов была выведена обобщенная формула, известная как коэффициент альфа. В этой формуле заме­нена на - сумму дисперсий балльных оценок по каждому заданию теста. Про­цедура вычислений состоит в нахождении дисперсии всех индивидуальных балльных оценок по каждому заданию с последующим суммированием этих дисперсий по всем заданиям. Полная формула коэффициента альфа выглядит следующим образом:

(20).

Кластерный анализ Горбатенко. Его суть состоит в применении математической процедуры «распознавания образа». Она позволяет «без учителя» выделять таксоны (кластеры), заpанее не задавая пpедполагаемое их количество и состав. Таксон включает в себя ряд тестовых заданий, которые фактически можно рассматривать как обладающие внутренним сходством, а значит, характеризующиеся надежностью-согласованностью.

Алгоритм данного метода предполагает:

а) составление «матрицы описания», которая характеризует конкретное состояние группируемых переменных (пунктов методики);

б) установление по определенным критериям численных значений связей (сходства) между всеми группируемыми переменными (пунктами методики) и построение «матрицы коэффициентов сходства»; в качестве меры «сходства» описаний i-го и j-го членов группы используется величина:

, (21)

где - число совпадений выборов в i-ом и j-ом столбцах, - число несовпадений выборов в i-ом и j-ом столбцах, - суммарное число выборов в i-ом и j-ом столбцах.

в) группировка переменных (пунктов) в таксоны и определение коэффициента плотности, характеризующего качество данной группировки; для того чтобы определить качество (плотность) полученных таксонов, используется мера D, которая вычисляется по формуле:

D= , (22)

где - число пунктов методики, - мера сходства между «центральным» и наиболее «удаленным» (несходным с центральным) пунктом.

г) в случае, если группировка производилась неоптимальным образом или качество группировки не удовлетворяет определенным критериям, производится перегруппировка переменных.

Для проведения расчетов используется специально разработанная компьютерная программа.

По методике (или каждой шкале многомерного теста) в программу дважды вводятся ответы всех испытуемых выборки по каждому заданию:

· ответы по совпадению с ключом (значимым вариантам ответов), которые индексируются «1»;

· ответы по несовпадению с ключом, которые индексируются «0».

По каждому способу обработки во внимание принимаются:

· количество таксонов и «доминирующий» (по численности и плотности) из них;

· не вошедшие ни в один таксон тестовые задания.

В окончательном варианте стимульного материала оставляют только те задания, которые входят в «главный» таксон каждого способа ввода данных (могут быть задания, которые одновременно входят в один и другой таксон).

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: