 |
225. Вспомогател. состояние для расчета угла поворота сечения?
|
|
|
|
225. . Вспомогател. состояние для расчета угла поворота сечения?
единичный силовой фактор - сосредоточенная пара
226. . Вспомогател. состояние для расчета взаимного лин. смещения?
2 сосредоточенные единич. силы 
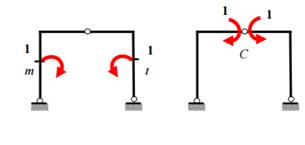
227. Вспомогател. состояние для расчета взаимного угла поворота?
2 сосредоточенные единич. пары
228. . Почему при расчете изгибн. перемещений пренебрегают N, Q?
прогибы, зависящие от Q, несравнимо малы по сравнению с прогибами и от изгибающих моментов, а N не вызывают изгиб. перемещений.
229. Перечислите формулы «перемножения» эпюр по методу Мора.
230. Как «перемножить» эпюры усилий по формуле Верещагина?
Умножить площадь эпюры от заданной нагрузки на координату эпюры от единичной силы под ц. т. площади первой эпюры.
231. Ограничение применимости формулы Верещагина?
1. Эпюра изгибающего момента от единичной нагрузки должна быть в виде одной прямой линии.
2. Изгибающий момент от внешней нагрузки в пределах участка должен иметь один знак.
3. Жесткость стержня в пределах участка должна быть постоянна, иначе интегрирование следует распространять отдельно на участки с постоянной жесткостью.
232. Как «перемножить» эпюры усилий по формуле Трапеций?
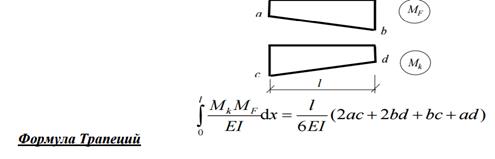
233. Ограничение применимости формулы Трапеций?
Формула трапеции перемножения эпюр применяется, только если обе эпюры линейны.
234. Как «перемножить» эпюры усилий по формуле Симпсона?
235. Как «перемножить» эпюры усилий по формуле Ньютона?
236. Формула расчета перемещений от действия температуры
интеграл Мора для определения температурных перемещений:
|
|
|
где α – коэффициент температурного расширения материала;
Интеграл значительно упрощается тогда, когда интегрирование ведётся для прямолинейных или ломаных стержней, имеющих по длине постоянное поперечное сечение. В этом случае интегралы могут быть определены, как площади единичных эпюр.
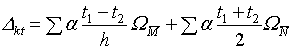, (5. 37)
где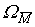 
и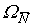 
- площади единичных эпюр 
и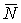 
.
(Пусть верхнее волокно элемента ds нагрето на t1, а нижнее - на t2. При этом t1 > t2. Распределение температуры по высоте сечения принято по прямолинейному закону. При температурном коэффициенте линейного расширения a верхнее волокно удлинится на at1ds, а нижнее - на at2ds. На уровне нейтральной оси это удлинение, что очевидно из рис. 5. 19, составит полусумму удлинений верхнего и нижнего волокон элемента ds.
. (5. 34)
Выражение (5. 34) соответствует тому состоянию элемента ds, при котором он по всей высоте сечения h получил равномерное изменение температуры. От неравномерного нагрева торцевые сечения элемента ds поворачиваются на угол
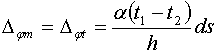. (5. 35)
Деформация сдвига в элементе ds не возникает, поэтому интергал Мора принимает такой вид).
237. Правило знаков при расчете перемещений от температуры?
При расчете перемещений методом Мора, если деформации элемента ds от температуры и от единичной силы одного знака, то соответствующие слагаемые в формуле положительны, и соответственно наоборот.
238. Какие деформации стержней вызывает температ. воздействие?
сечения элементов сооружения поступательно перемещаются (линейные перемещения) и поворачиваются (угловые перемещения).
239. Формула для определения перемещений от смещения опор?
∆ k∆ = – ∑ Ri ∙ ∆ i
∆ k∆ – искомое перемещение какой-либо точки (сечения) в заданном направлении i;
Ri – реакция в i-й связи, которая возникает от действия единичной нагрузки, приложенной в направлении искомого перемещения;
∆ i – заданное смещение j-й связи (опоры). Чем вызвано это смещение не имеет значения.
|
|
|
|
|
|
