Логические основы компьютера

 

Всякое устройство ЭВМ, выполняющее некоторое действие над цифровыми сигналами, можно рассматривать как функциональный преобразователь, на входы которого с помощью цифровых сигналов подаются значения аргументов функции (исходные двоичные числа), а на выходах получают значения функций, реализующих указанное действие для этих аргументов (выходные двоичные числа).

Логический элемент компьютера - это часть электронной логической схемы, которая реализует элементарную логическую функцию.

1) Логический элемент «И» (конъюнктор). Выдает на выходе значение логического произведения входных сигналов

 

Рис. 1

 

2) Логический элемент «ИЛИ» (дизъюнктор). Выдает на выходе значение логического сложения входных сигналов

Рис.2

 

3) Логический элемент «НЕ» (инвертор). Выдает на выходе сигнал, противоположный сигналу на входе.

 

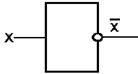
Рис. 3

Пример. Определить структурную формулу по заданной функциональной схеме

 

 

 

Решение:

1. Переменные А и В входят в «коробочку» ИЛИ, полученная формула на выходе – (А Ú В)

2. Пройдя «коробочку» ИЛИ сигнал заходит в «коробочку» НЕ, полученная формула на выходе – не (А Ú В)

3. Переменная В тоже проходит через «коробочку» НЕ, полученная формула на выходе – не В

4. Далее на пути встречается «коробочка» И, пройдя через которую переменные приходят к виду F = не (А Ú В) и (не В)

 

Запишем соответствующие формулы на схеме:

 

ПРИМЕРЫ ТИПОВЫХ РЕШЕНИЙ

ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА ПО ТЕМЕ «СИСТЕМА СЧИСЛЕНИЯ»

Задача №1

Даны два числа a=D7₁₆ и b=331₈. Необходимо определить какое из чисел, записанных в двоичной системе счисления, удовлетворяет неравенству a<c<b?

1) 11011001₂

2) 11011100₂

3) 11010111₂

4) 11011000₂

Общий подход: перевести все числа (и исходные данные, и ответы) в одну (любую!) систему счисления и сравнить.

 

Решение (вариант 1, через десятичную систему):

1)

2)

3) переводим в десятичную систему все ответы:

11011001₂ = 217,

11011100 ₂= 220,

11010111₂ = 215,

11011000₂=216

4) очевидно, что между числами 215 и 217 может быть только 216

5) таким образом, верный ответ – 4.

 

Решение (вариант 2, через двоичную систему):

1) 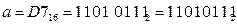(каждая цифра шестнадцатеричной системы отдельно переводится в четыре двоичных – тетраду);

2) (каждая цифра восьмеричной системы отдельно переводится в три двоичных – триаду, старшие нули можно не писать);

3) теперь нужно сообразить, что между этими числами находится только двоичное число 11011000₂ – это ответ 4.

 

Решение (вариант 3, через восьмеричную систему):

1) (сначала перевели в двоичную систему, потом двоичную запись числа разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, так как для чисел от 0 до 7 их восьмеричная запись совпадает с десятичной);

2) , никуда переводить не нужно;

3) переводим в восьмеричную систему все ответы:

11011001₂ = 011 011 001₂ = 331₈ (разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, как в п. 1)

11011100 ₂= 334₈, 11010111₂ = 327₈, 11011000₂=330₈

4) в восьмеричной системе между числами 327₈ и 331₈ может быть только 330₈

5) таким образом, верный ответ – 4.

 

Решение (вариант 4, через шестнадцатеричную систему):

1) никуда переводить не нужно;

2) 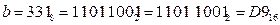(сначала перевели в двоичную систему, потом двоичную запись числа разбили на тетрады справа налево, каждую тетраду перевели в шестнадцатеричную систему; при этом тетрады можно переводить из двоичной системы в десятичную, а затем заменить все числа, большие 9, на буквы – A, B, C, D, E, F);

3) переводим в шестнадцатеричную систему все ответы:

11011001₂ = 1101 1001₂ = D9₁₆ (разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F, как в п. 1)

11011100 ₂= DC₁₆, 11010111₂ = D7₁₆, 11011000₂=D8₁₆

4) в шестнадцатеричной системе между числами D7₁₆ и D9₁₆ может быть только D8₁₆

5) таким образом, верный ответ – 4.

Задача №2.

Даны два числа х и у. Чему равна сумма этих чисел, если и ?

1) 121₈

2) 171₈

3) 69₁₆

4) 1000001₂

Общий подход: перевести оба исходных числа и ответы в одну (любую!) систему счисления, и выполнить сложение

 

Решение (вариант 1, через десятичную систему):

1.

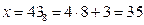
2.

3. сложение: 35 + 86 = 121

4a) переводим результат во все системы, в которых даны ответы (пока не найдем нужный):

121 = 1111001₂ = 171₈ = 79₁₆

4b) или переводим все ответы в десятичную систему

121₈ = 81,

171₈ = 121,

69₁₆ = 105,

1000001₂ = 65

5) таким образом, верный ответ – 2.

Решение (вариант 2, через двоичную систему):

1) (каждая цифра восьмеричной системы отдельно переводится в три двоичных – триаду, старшие нули можно не писать)

2) (каждая цифра шестнадцатеричной системы отдельно переводится в четыре двоичных – тетраду)

3) складываем

100011₂

+ 1010110₂

1111001₂

4) переводим все ответы в двоичную систему

121₈ = 001 010 001₂ = 1010001₂ (по триадам)

171₈ = 001 111 001₂ = 1111001₂ (по триадам)

69₁₆ = 0110 1001₂ = 1101001₂ (по тетрадам)

1000001₂ не нужно переводить

5) правильный ответ – 2.

Решение (вариант 3, через восьмеричную систему):

1) , никуда переводить не нужно

2) (сначала перевели в двоичную систему, потом двоичную запись числа разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, так как для чисел от 0 до 7 их восьмеричная запись совпадает с десятичной)

3) складываем

43₈

+ 126₈

171₈

4) видим, что такой ответ есть, это ответ 2.

Решение (вариант 4, через шестнадцатеричную систему):

1) (сначала перевели в двоичную систему, потом двоичную запись числа разбили на тетрады справа налево, каждую тетраду перевели в шестнадцатеричную систему; при этом тетрады можно переводить из двоичной системы в десятичную, а затем заменить все числа, большие 9, на буквы – A, B, C, D, E, F)

2) , никуда переводить не нужно

3) складываем

23₁₆

+ 56₁₆

79₁₆

4) переводим в шестнадцатеричную систему все ответы:

121₈ = 001 010 001₂ = 0101 0001₂ = 51₁₆ (перевели в двоичную систему по триадам, разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F)

171 ₂ = 001 111 001₂ = 0111 1001₂ = 79₁₆,

69₁₆, переводить не нужно

1000001₂ = 0100 0001₂ = 41₁₆

 

5) таким образом, верный ответ – 2.

Задача №3

Пример 1. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?

 

Общий подход:

¾ вспомним алгоритм перевода числа из десятичной системы в систему с основанием , из него следует, что младшая цифра результата – это остаток от деления исходного числа на , а две младших цифры – это остаток от деления на и т.д.

¾ в данном случае , остаток от деления числа на должен быть равен 11₄ = 5

¾ потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16

Решение (вариант 1, через десятичную систему):

1. общий вид чисел, которые дают остаток 5 при делении на 16:

где – целое неотрицательное число (0, 1, 2, …)

2. среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при ) и 21 (при )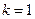

3. таким образом, верный ответ – 5, 21.

Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):

1) переведем 25 в четверичную систему счисления: 25 = 121₄, все интересующие нас числа не больше этого значения

2) из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:

это 11₄ = 5 и 111₄ = 21

3) таким образом, верный ответ – 5, 21.

 

Пример 2. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

Общий подход:

¾ здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через

¾ поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть

¾ вспомним алгоритм перевода числа из десятичной системы в систему с основанием (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на

Решение:

1) итак, нужно найти все целые числа , такие, что остаток от деления 23 на равен 2, или (что то же самое)

(*)

где – целое неотрицательное число (0, 1, 2, …);

2) сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа

3) из формулы (*) получаем , так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2

4) в этой задаче есть только три таких делителя: и

5) таким образом, верный ответ – 3, 7, 21.

Задача №4.

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.

Общий подход:

¾ неизвестно основание системы счисления, мы обозначим его через

¾ пока будем считать, что запись числа 31 в системе с основанием состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через ) нужно найти:

2 1 0 ← разряды

31 = k 1 1_N = k·N² + N¹ + N⁰ = k·N² + N + 1

¾ можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить как при некотором целом ; например, для числа с пятью разрядами получаем:

4 3 2 1 0 ← разряды

31 = k₄ k₃ k₂ 1 1_N = k₄·N⁴ + k₃·N³ + k₂·N² + N¹ + N⁰

= k·N² + N + 1

для (из первых трех слагаемых вынесли общий множитель )

Решение:

1) итак, нужно найти все целые числа , такие что

(**)

где – целое неотрицательное число (0, 1, 2, …);

2) сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа

3) из формулы (**) получаем , так что задача сводится к тому, чтобы найти все делители числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом , то есть, – целое число

4) выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30

5) из всех этих делителей только для 2, 3, 5 и 30 значение – целое число (оно равно соответственно 7, 3, 1 и 0)

6) таким образом, верный ответ – 2, 3, 5, 30.

 

 

ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА ПО ТЕМЕ «КОДИРОВАНИЕ ИНФОРМАЦИИ»

 

Задача №1

Тема: Кодирование текстовой информации. Кодировка ASCII. Основные кодировки кириллицы.

Что нужно знать:

¾ все символы кодируются одинаковым числом бит[3] (алфавитный подход)

¾ чаще всего используют кодировки, в которых на символ отводится 8 бит (8-битные) или 16 бит (16-битные)

¾ при измерении количества информации принимается, что в одном байте 8 бит, а в одном килобайте (1 кбайт) – 1024 байта, в мегабайте (1Мбайт) – 1024 кбайта[4]

¾ после знака препинания внутри (не в конце!) текста ставится пробел

¾ чтобы найти информационный объем текста I, нужно умножить количество символов N на число бит на символ K: I = N * K

¾ две строчки текста не могут занимать 100 кбайт в памяти

 

Пример 1. Определите информационный объем текста

Бамбарбия! Кергуду!

1) 38 бит

2) 144 бита

3) 152 бита

4) 19 бит

 

Решение:

6) в этом тексте 19 символов (обязательно считать пробелы и знаки препинания)

7) если не дополнительной информации, считаем, что используется 8-битная кодировка (чаще всего явно указано, что кодировка 8- или 16-битная)

8) поэтому в сообщении 19*8 = 152 бита информации (ответ 3).

Пример 2. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 480 бит. Какова длина сообщения в символах?

Решение:

1) обозначим количество символов через N

2) при 16-битной кодировке объем сообщения – 16*N бит

3) когда его перекодировали в 8-битный код, его объем стал равен– 8*N бит

4) таким образом, сообщение уменьшилось на 16*N – 8*N = 8*N = 480 бит

5) отсюда находим N = 480/8 = 60 символов.

 

Задача №2

Тема: Вычисление информационного объема сообщения.

Что нужно знать:

¾ с помощью K бит можно закодировать Q = 2^K различных вариантов (чисел)

¾ таблица степеней двойки, она же показывает, сколько вариантов Q можно закодировать с помощью K бит:

 

K, бит
Q, вариантов

 

¾ при измерении количества информации принимается, что в одном байте 8 бит, а в одном килобайте (1 кбайт) – 1024 байта, в мегабайте (1Мбайт) – 1024 кбайта[5]

¾ чтобы найти информационный объем сообщения (текста) I, нужно умножить количество символов (отсчетов) N на число бит на символ (отсчет) K: I = N * K

¾ две строчки текста не могут занимать 100 кбайт в памяти

¾ мощность алфавита – это количество символов в этом алфавите

 

Пример 1. В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?

1) 70 бит

2) 70 байт

3) 490 бит

4) 119 байт

Решение:

1) велосипедистов было 119, у них 119 разных номеров, то есть, нам нужно закодировать 119 вариантов

2) по таблице степеней двойки находим, что для этого нужно минимум 7 бит (при этом можно закодировать 128 вариантов, то есть, еще есть запас); итак, 7 бит на один отсчет

3) когда 70 велосипедистов прошли промежуточный финиш, в память устройства записано 70 отсчетов

4) поэтому в сообщении 70*7 = 490 бит информации (ответ 3).

 

Пример 2. Объем сообщения, содержащего 4096 символов, равен 1/512 части Мбайта. Какова мощность алфавита, с помощью которого записано это сообщение?

1) 8

2) 16

3) 4096

4) 16384

 

Решение (вариант 1):

1) в сообщении было 4096 = 2¹² символов

2) объем сообщения

1/512 Мбайта = 2²³ / 512 бита = 2²³ / 2⁹ бита = 2¹⁴ бита (= 16384 бита!)

3) место, отведенное на 1 символ:

2¹⁴ бита / 2¹² символов = 2² бита на символ = 4 бита на символ

4) 4 бита на символ позволяют закодировать 2⁴ = 16 разных символов

5) поэтому мощность алфавита – 16 символов

6) правильный ответ – 2.

Решение (вариант 2, предложен В.Я. Лаздиным):

1) объем сообщения

1/512 Мбайт = 1024/512 кбайт = 2 кбайт = 2048 байт

2) на 1 символ приходится 2048 байт / 4096 = 1/2 байта = 4 бита

3) 4 бита на символ позволяют закодировать 2⁴ = 16 разных символов

4) поэтому мощность алфавита – 16 символов

5) правильный ответ – 2.

 

Пример 3. В корзине лежат 32 клубка шерсти, из них 4 красных. Сколько бит информации несет сообщение о том, что достали клубок красной шерсти?

1) 2

2) 3

3) 4

4) 32

Решение (вариант 1):

1) красные клубки шерсти составляют 1/8 от всех, …

2) поэтому сообщение о том, что первый вынутый клубок шерсти – красный, соответствует выбору одного из 8 вариантов

3) выбор 1 из 8 вариантов – это информация в 3 бита (по таблице степеней двойки)

4) правильный ответ – 2.

Решение (вариант 2, использование формулы Шеннона):

1) красные клубки шерсти составляют 1/8 от всех, поэтому вероятность того, что первый вынутый клубок шерсти – красный, равна 1/8

2) по формуле Шеннона находим количество информации в битах:

бита.

3) правильный ответ – 2.

 

Задача №3

Тема: Кодирование и декодирование информации.

Что нужно знать:

¾ кодирование – это перевод информации с одного языка на другой (запись в другой системе символов, в другом алфавите)

¾ обычно кодированием называют перевод информации с «человеческого» языка на формальный, например, в двоичный код, а декодированием – обратный переход

¾ один символ исходного сообщения может заменяться одним символом нового кода или несколькими символами, а может быть и наоборот – несколько символов исходного сообщения заменяются одним символом в новом коде (китайские иероглифы обозначают целые слова и понятия)

¾ кодирование может быть равномерное и неравномерное; при равномерном кодировании все символы кодируются кодами равной длины; при неравномерном кодировании разные символы могут кодироваться кодами разной длины, это затрудняет декодирование

 

Пример 1. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится

1) 4B₁₆

2) 411₁₆

3)BACD₁₆

4) 1023₁₆

Решение:

1) из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный

2) последовательность БАВГ кодируется так: 01 00 10 11 = 1001011

3) разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем

1001011 = 0100 1011₂ = 4B₁₆

4) правильный ответ – 1.

Пример 2.

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице:

A	B	C	D	E

 

Определить, какой набор букв закодирован двоичной строкой 0110100011000

1) EBCEA

2) BDDEA

3) BDCEA

4) EBAEA

 

Решение (вариант 1, декодирование с начала):

7) здесь используется неравномерное кодирование, при котором декодирование может быть неоднозначным, то есть, заданному коду может соответствовать несколько разных исходных сообщений

8) попробуем декодировать с начала цепочки, первой буквой может быть B или E, эти случаи нужно рассматривать отдельно

9) пусть первая буква – E с кодом 011, тогда остается цепочка 0100011000

¾ для кода 0100011000 первой буквой может быть только B с кодом 01, тогда остается 00011000 (начало исходной цепочки – EB?)

¾ для кода 00011000 первой буквой может быть только A с кодом 000, тогда остается 11000, а эта цепочка не может быть разложена на заданные коды букв

¾ поэтому наше предположение о том, что первая буква – E, неверно

¾ пусть первая буква – B с кодом 01, тогда остается цепочка 10100011000

¾ для кода 10100011000 первой буквой может быть только D с кодом 10, тогда остается 100011000 (можно полагать, что начало исходной цепочки – BD?)

¾ для кода 100011000 первой буквой может быть только С с кодом 100, тогда остается 011000 (начало исходной цепочки – BDC?)

Несмотря на то, что среди ответов есть единственная цепочка, которая начинается с BDC, здесь нельзя останавливаться, потому что «хвост» цепочки может «не сойтись»

¾ для кода 011000 на первом месте может быть B (код 01) или E (011); в первом случае «хвост» 1000 нельзя разбить на заданные коды букв, а во втором – остается код 000 (буква А), поэтому исходная цепочка может быть декодирована как BDCEA

10) правильный ответ – 3

Решение (вариант 2, декодирование с конца):

1) для кода 0110100011000 последней буквой может быть только А (код 000), тогда остается цепочка 0110100011

2) для 0110100011 последней может быть только буква E (011), тогда остается цепочка 0110100

3) для 0110100 последней может быть только буква C (100), тогда остается цепочка 0110

4) для 0110 последней может быть только буква D (10), тогда остается 01 – это код буквы B

5) таким образом, получилась цепочка BDCEA

6) правильный ответ – 3

 

Задача №4

Тема: Кодирование информации.

Для хранения растрового изображения размером 32×32 пикселя отвели 512 байтов памяти. Каково максимально возможное число цветов в палитре изображения?

1) 256

2) 2

3) 16

4) 4

Общий подход:

В таких задачах вся игра идет на двух формулах: 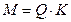и Поэтому нужно:

9) найти общее количество пикселей Q

10) перевести объем памяти M в биты

11) найти количество бит на пиксель

12) по таблице степеней двойки найти количество цветов N

Решение:

1) находим общее количество пикселей

2) находим объем памяти в битах байт байт бит бит

3) определяем количество бит на пиксель: бита на пиксель

4) по таблице степеней двойки находим, что 4 бита позволяют закодировать 2⁴ = 16 цветов

5) поэтому правильный ответ – 3.

 

Пример 2. Для кодирования цвета фона страницы Интернет используется атрибут bgcolor="#ХХХХХХ", где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной RGB-модели. Какой цвет будет у страницы, заданной тэгом <body bgcolor="#FFFFFF">?

1) белый

2) зеленый

3)красный

4) синий

Решение:

1) значение FF₁₆ = 255 соответствует максимальной яркости, таким образом, яркость всех составляющих максимальна, это белый цвет

2) правильный ответ – 1

 

Задача №5

Тема: Определение скорости передачи информации при заданной пропускной способности канала.

 

Пример 1. Скорость передачи данных через ADSL-соединение равна 128000 бит/c. Через данное соединение передают файл размером 625 кбайт. Определите время передачи файла в секундах.

Решение:

1. выделим в заданных больших числах степени двойки и переведем размер файла в биты, чтобы «согласовать» единиц измерения:

128000 бит/c = 128 · 1000 бит/с = 2⁷ · 125 · 8 бит/с = 2⁷ · 5³ · 2³ бит/с = 2¹⁰ · 5³ бит/с

625 кбайт = 5⁴ кбайт = 5⁴ · 2¹³ бит

2. чтобы найти время передачи в секундах, нужно разделить размер файла на скорость передачи:

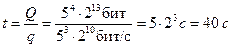
3. таким образом, ответ – 40 с.

 

Пример 2. Скорость передачи данных через ADSL-соединение равна 512 000 бит/c. Передача файла через это соединение заняла 1 минуту. Определить размер файла в килобайтах.

Решение:

1) выделим в заданных больших числах степени двойки; переведем время в секунды (чтобы «согласовать» единицы измерения), а скорость передачи – в кбайты/с, поскольку ответ нужно получить в кбайтах:

1 мин = 60 с = 4 · 15 с = 2² · 15 с

512000 бит/c = 512 · 1000 бит/с = 2⁹ · 125 · 8 бит/с = 2⁹ · 5³ · 2³ бит/с
= 2¹² · 5³ бит/с = 2⁹ · 5³ байт/с = кбайт/с = кбайт/с

2) чтобы найти время объем файла, нужно умножить время передачи на скорость передачи:

кбайт/с кбайт кбайт

3) таким образом, ответ – 3750 кбайт.

 

 

ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА ПО ТЕМЕ «АЛГЕБРА ЛОГИКИ»

Задача №1

Укажите, какое логическое выражение равносильно выражению AÙ(BÚC)

1) A Ú B Ú C

2) A Ú B Ú C

3) A Ù B Ù C

4) A Ù B Ù C

Решение (использование законов де Моргана):

1. Перепишем заданное выражение и ответы в других обозначениях:
заданное выражение
ответы: 1) 2) 3) 4)

2. Посмотрев на заданное выражение, видим инверсию (операцию «НЕ») для сложного выражения в скобках, которую раскрываем по формуле де Моргана,

а затем используем закон двойного отрицания по которому :

3. Таким образом, правильный ответ – 3.

Задача №2

Сколько различных решений имеет уравнение ((K\/L) /\ (M\/N)) = 1, где K, L, M, N – логические переменные?

В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.

Решение

((K\/L) /\ (M\/N)) = 1

K	L	M	N	K\/L	M\/N	(K\/L) /\ (M\/N)

 

Ответ: 9

Задача №3

Пример 1. Для какого из указанных значений числа X истинно высказывание ((X>2) -> (X>3))

1) 1

2) 2

3) 3

4) 4

Решение

1) определим порядок действий: сначала вычисляются результаты отношений в скобках, затем выполняется импликация (поскольку есть «большие» скобки), затем – отрицание (операция «НЕ») для выражения в больших скобках

2) выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); сначала определяем результаты сравнения в двух внутренних скобках:

 

X	X > 2	X > 3	(X > 2)→(X > 3)	((X > 2)→(X > 3))

1) по таблице истинности операции «импликация» находим третий столбец (значение выражения в больших скобках), применив операцию «импликация» к значениям второго и третьего столбцов (в каждой строке):

 

X	X > 2	X > 3	(X > 2)→(X > 3)	((X > 2)→(X > 3))

 

2) значение выражения равно инверсии третьего столбца (меняем 1 на 0 и наоборот):

 

X	X > 2	X > 3	(X > 2)→(X > 3)	((X > 2)→(X > 3))

 

3) таким образом, ответ – 3.

Решение (вариант 2, упрощение выражения):

1) обозначим простые высказывания буквами:

A = X > 2, B = X > 3

2) тогда можно записать все выражение в виде

(A → B) или

 

3) выразим импликацию через «ИЛИ» и «НЕ» (см. выше):

(A → B)= (A Ú B) или

 

4) раскрывая по формуле де Моргана операцию «НЕ» для всего выражения, получаем

(A Ú B)= A Ù B или

5) таким образом, данное выражение истинно только тогда, когда A истинно (X > 2), а B – ложно (X ≤ 3), то есть для всех X, таких что 2 < X ≤ 3

6) из приведенных чисел только 3 удовлетворяет этому условию,

7) таким образом, ответ – 3.

Выводы:

1) в данном случае, наверное, проще первый вариант решения (прямая подстановка всех предложенных ответов)

2) второй вариант позволяет не только проверить заданные значения, но и получить общее решение – все множество X, для которых выражение истинно; это более красиво для человека, обладающего математическим складом ума.

Задача №4

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

 

X	Y	Z	F

 

Какое выражение соответствует F?

1)X \/ Y \/ Z

2) X /\ Y /\ Z

3) X /\ Y /\ Z

4) X \/ Y \/ Z

 

Решение

Рассмотрим выражение X \/ Y \/ Z

1) X=0, Y=0, Z=0, F=0

0 \/ 0 \/0=0

2) X=1, Y=1, Z=0, F=1

1 \/1 \/0=1

3) X=1, Y=0, Z=0, F=1

1 \/0 \/0=1

Ответ: 4

 

Задача №5

Три школьника, Миша (М), Коля (К) и Сергей (С), остававшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:

Миша: «Я не бил окно, и Коля тоже…»

Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!»

Сергей: «Я не делал этого, стекло разбил Миша».

Стало известно, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил. Зная это, директор смог докопаться до истины.

Кто разбил стекло в классе? В ответе запишите только первую букву имени.

Решение

	М	К	С
М
К
С
истинно

 

Значит, Сергей сказал правду, Коля соврал, Миша в одной части заявления соврал, а другое его высказывание истинно

Сергей: Сергей не бил, Миша бил;

Коля: Миша бил, Сергей не бил;

Миша: Коля не бил, Миша бил.

Ответ: М

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: