 |
Механический смысл производной
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ КЫРГЫЗСКОЙ РЕСПУБЛИКИ
КЫРГЫЗСКО – РОССИЙСКИЙ СЛАВЯНСКИЙ УНИВЕРСИТЕТ
Медицинский факультет
Кафедра физики, медицинская информатики и биологии
ВЫСШАЯ МАТЕМАТИКА
Учебное пособие
Бишкек 2012
УДК
ББК
Л
Составители: доцент, А.А. Сорокин; доцент, Т.И. Сологубова; доцент, И.Р. Тупеев; ст. преп., Н.А. Абдукаримова; ст. преп., Р.Б. Молдонасиров
Рекомендовано к изданию Ученым советом КРСУ
(пр. №__ от ……..)
Рецензенты:
Допущено Министерством образования и науки Кыргызской Республики в качестве учебного пособия для студентов высших учебных заведений
(пр. №………)
Л…. ВЫСШАЯ МАТЕМАТИКА: Учеб. Пособие/Сост.А.А. Сорокин, Т.И. Сологубова, И.Р. Тупеев, Н.А. Абдукаримова, Р.Б. Молдонасиров.-Бишкек: КРСУ, 2012.-…с.
ISBN …………………
Работа представляет собой учебное пособие, которое поможет студентам-медикам освоить основы высшей математики, математической статистики и подготовиться к практическим занятиям.
К ……….. УДК
ББК
ISBN ………………… ©КРСУ, 2012
©А.А. Сорокин,
Т.И. Сологубова,
И.Р. Тупеев,
Н.А. Абдукаримова,
Р.Б. Молдонасиров, 2012
АННОТАЦИЯ
Математическая подготовка студентов медицинских вузов дает возможность более глубоко изучить курсы медицинской и биологической физики, информатики, бионеорганической и биоорганической химии, технологии лекарственных веществ, рентгенологии и другие медико-биологические дисциплины.
Теория курса «Высшая математика» охватывает те разделы математики, которые находят применение в медицине, и помогут студентам приобрести математические навыки для дальнейшей работы.
|
|
|
Производная функции может быть использована при математическом описании динамики химических реакций, при нахождении градиентов скорости, давления, концентрации, температуры и других величин.
Интегральное исчисление является составной частью математического анализа и применяется при решении многих задач химии, биологии, медицины именно в тех случаях, когда по известной производной требуется найти вид самой функции.
Дифференциальные уравнения используются при изучении явлений и процессов во всех областях знаний, в том числе и в медицине. Сформулировав задачу на языке дифференциальных уравнений, специалист–медик получает готовый аппарат для численного решения задачи, изучения качественных особенностей этого решения. Кроме того, дифференциальные уравнения являются одним из средств математического моделирования. Пользуясь ими, устанавливается связь между переменными величинами, характеризующими данный процесс или явление.
Теория вероятностей изучает закономерности, присущие случайным событиям, величинам и процессам массового характера. Теория вероятностей нашла применение в теории эпидемий, в разработке математических методов медицинской диагностики, в организации здравоохранения и т.д.
Математическая статистика - раздел математики, непосредственно примыкающий к теории вероятностей. Медицинские задачи, которые решаются с её помощью, принимают ту или иную форму в зависимости от характера вопроса и объема накопленного опытного материала.
Наиболее важными для студентов-медиков при изучении дисциплины “Высшая математика” являются знания статистических методов в клинических и лабораторно-экспериментальных исследованиях. Многочисленность и многообразие количественных показателей, получаемых при обследовании различных систем и органов человека в клинической практике и в эксперименте, вызывают необходимость их обобщения и поиска наиболее приемлемых математических и математико-статистических критериев, удовлетворяющих научным требованиям медицины.
|
|
|
СОДЕРЖАНИЕ
Тема №1. Призводная и дифференциал функции...............................................................6 - 20
Тема №2. Применение производных к исследованию функций.....................................21 - 29
Тема №3. Неопределенный интеграл.................................................................................30 - 37
Тема №4. Определенный интеграл.....................................................................................38 - 45
Тема №5. Дифференциальные уравнения..........................................................................46 - 60
Тема №6. Составление и решение дифференциальных уравнений на примерах задач физического, химического, фармацевтического и медико-биологического содержания............................................................................................................................61 - 67
Тема №7. Элементы теории вероятностей.........................................................................68 - 81
Тема №8. Случайные величины. Закон нормального распределения случайных величин................................................................................................................................82 - 101
Тема №9. Элементы математической статистики........................................................102 - 121
Тема №10. Теория корреляции..........................................................................................122-131
Заметки для аспирантов и соискателей……………………………………………..…..132-160
Приложение 1.............................................................................................................................161
Приложение 2 ………………………… …… …………..........................................................162
Приложение 3…………………………………………………….............................................164
Приложение 4…………………………………………………….............................................165
Приложение 5……………………………………………………….........................................166
Приложение 6……………………………………………………….........................................166
Приложение 7………………………………………………………….....................................167
Приложение 8………………………………………………………….....................................167
Приложение 9.............................................................................................................................168
Приложение 10...........................................................................................................................169
ТЕМА №1
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Понятие производной функции и понятие дифференциала функции являются одними из основных понятий математического анализа. Производная характеризует быстроту изменения функции при изменении её аргумента и может быть использована при математическом описании динамики химических реакций, при нахождении градиентов скорости, давления, концентрации, температуры и других величин.
|
|
|
Цель занятия:
· Уметь объяснить физический смысл производной первого и второго порядков.
· Научиться находить производные от элементарных и сложных функций.
· Научиться находить производные высших порядков.
· Научиться находить дифференциалы функций.
· Научиться приближенно вычислять функции с помощью дифференциала.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Пусть на интервале ]а,в[ определена функция у=f(x). При приращении аргумента Dх функция получит приращение Df, которое определится равенством: Df=f(x+Dx)-f(x), тогда отношение:
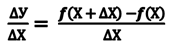
выражает среднюю скорость изменения функции f(x) относительно аргумента х на интервале ]х, х+Dх[.
Предел отношения приращения функции к приращению аргумента, когда Dх®0, при условии, что этот предел существует, называется производной функции в точке хÎ ]а,в[:

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Решение задачи о нахождении скорости различных процессов приводит к понятию производной функции. Рассмотрим скорость прямолинейного движения. Пусть тело, двигаясь с переменной скоростью, прошло путь S, тогда средняя скорость равна:
 ,
,
где t- время движения тела. Разобьем весь путь на n отдельных участков: DS1, DS2,…,DSn, пройденные соответственно за время: Dt1, Dt2,..,Dtn, тогда скорости на этих участках:

Если величину участков уменьшить, т.е. задать Dt®0, то средняя скорость стремится к пределу, который представляет собой скорость движения тела в данный момент времени или мгновенную скорость:

Таким образом, мгновенная скорость есть предел отношения приращения пути к приращению времени, когда приращение времени стремится к нулю.
- ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Пусть функция у=f(x) задана графически. Возьмем на кривой произвольно точку М(х,у). Зададим приращение аргументу Dх, тогда функция получит приращение Dу и на графике мы получим точку М1 с координатами (х+Dх;у+Dу). Проведем секущую ММ1 и обозначим угол наклона секущей к оси Ох через j: tgj=Dy/Dx
|
|
|

Рис 1. Геометрический смысл производной и дифференциала функции.
Пусть Dх® 0, тогда точка М1 будет стремиться к точке М, величина угла j будет изменяться. При приближении ММ1 к касательной МТ, угол j приближается к углу a, следовательно, tga равен угловому коэффициенту касательной:

Таким образом, геометрический смысл производной заключается в том, что она есть угловой коэффициент касательной к графику функции в этой точке.
|
|
|


