 |
Задачи для домашнего решения
|
|
|
|
1. Найти общее и частное решение:
а)  при
при 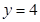 , если
, если  ;
;
б) 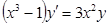 при
при  , если
, если 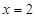 ;
;
в) 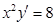 при
при  , если
, если 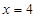 ;
;
г)  при
при 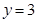 , если
, если 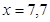 ;
;
д) 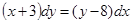 при
при  , если
, если 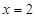 ;
;
е) 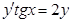 при
при 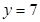 , если
, если  .
.
2.Найти общее решение:
а)  ;
;
б) 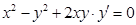 ;
;
в) 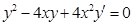 .
.
3.Найти общее решение:
а)  ; г)
; г) 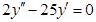 ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е) 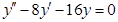 .
.
4.Найти общее решение:
а) 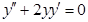 ;
;
б) 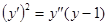 ;
;
в) 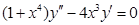 ;
;
г) 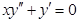 ;
;
д)  ;
;
е)  .
.
Задачи для решения на практических занятиях
- Найти общее и частное решения:
а) 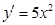 при
при 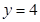 , если
, если 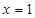 ;
;
б)  при
при  , если
, если 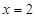 ;
;
в) 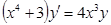 при
при  , если
, если  ;
;
г) 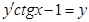 при
при 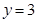 , если
, если 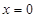 ;
;
д) 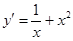 при
при 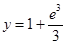 , если
, если  ;
;
е) 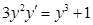 при
при  , если
, если 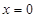 ;
;
ж) 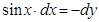 при
при 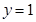 , если
, если 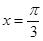 ;
;
з) 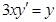 при
при  , если
, если 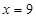 ;
;
и)  при
при 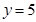 , если
, если  ;
;
к)  при
при 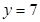 , если
, если  .
.
2. Найти общее решение:
а)  ;
;
б) 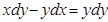 ;
;
в) 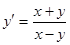 ;
;
г)  ;
;
д) 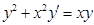 .
.
3. Найти общее решение:
а) 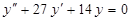 ; к)
; к)  ;
;
б) 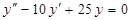 ; л)
; л)  ;
;
в) 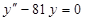 ; м)
; м) 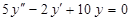 ;
;
г) 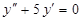 ; н)
; н)  ;
;
д)  ; о)
; о) 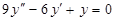 ;
;
е) 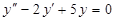 ; п)
; п) 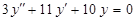 ;
;
ж)  ; р)
; р)  ;
;
з) 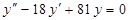 ; с)
; с) 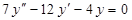 ;
;
и)  ; т)
; т) 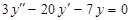 .
.
4. Найти общее решение:
а)  ;
;
б) 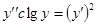 ;
;
в) 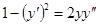 ;
;
г)  ;
;
д) 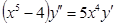 ;
;
е) 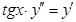 ;
;
ж) 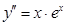 ;
;
з) 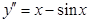 ;
;
к)  .
.
ТЕМА №6
СОСТАВЛЕНИЕ И РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ НА ПРИМЕРАХ ЗАДАЧ ФИЗИЧЕСКОГО, ХИМИЧЕСКОГО, ФАРМАЦЕВТИЧЕСКОГО И МЕДИКО-БИОЛОГИЧЕСКОГО СОДЕРЖАНИЯ
Дифференциальные уравнения являются одним из средств математического моделирования. Пользуясь ими, мы устанавливаем связь между переменными величинами, характеризующими данный процесс или явление.
Пример 1: Зависимость числа нераспавшихся ядер атомов радиоактивных элементов от времени. (Основной закон радиоактивного распада).
Ядра атомов радиоактивных элементов с течением времени распадаются. Опытным путем установлено, что скорость распада пропорциональна числу нераспавшихся в данный момент ядер атомов. В аналитической форме это можно записать так:  , (1)
, (1)
где N - число нераспавшихся в данный момент ядер атомов;
t - время;
l - постоянная распада.
Минус означает, что с течением времени число нераспавшихся ядер атомов уменьшатся.
Установим зависимость числа нераспавшихся ядер атомов радиоактивного вещества от времени, если при t=0 число нераспавшихся ядер атомов N=N0
|
|
|
В исходном уравнении (1) разделим переменные и проинтегрируем левую часть по N, а правую часть по t:

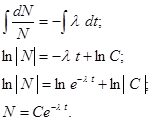
Полагая в последнем уравнении что при t = 0 и N = N0, находим C=N0. Тогда
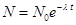 (2)
(2)
N0 -начальное число ядер.
Формула (2) отражает зависимость числа нераспавшихся ядер атомов радиоактивного вещества от времени, график этой зависимости показан на рисунке 1.
Из формулы (2) можно определить период полураспада Т, т.е. время, в течение которого число ядер атомов уменьшается вдвое. Положив в формуле (2) t=T и  , получим:
, получим:
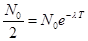 ;
;  .
.
Прологарифмируем последнее выражение:  , откуда
, откуда 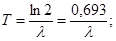

Рис 1. График зависимости числа не распавшихся ядер от времени
Из последней формулы видно, что период полураспада связан с постоянной распада и является характеристикой данного радиоактивного вещества.
Пример 2. Кинетика химических процессов
В общем случае скорость химической реакции зависит от концентрации реагирующих веществ. Уравнение, выражающее зависимость скорости реакции от концентрации каждого вещества, влияющего на скорость, называется кинетическим дифференциальным уравнением химического процесса. Рассмотрим химические процессы первого порядка.
Скорость, реакции первого порядка выражается уравнением:
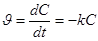 , (1)
, (1)
где C - концентрация реагирующего вещества:;
k - постоянная скорости реакции.
Минус в уравнении (1) означает, что концентрация реагирующего вещества с течением времени убывает.
В дифференциальном уравнении (1) разделим переменные и проинтегрируем его:

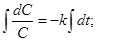

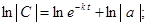
 ,
,
где a - постоянная интегрирования.
Полагая при t=0, C=C0, получаем a=C0, следовательно,
 , (2)
, (2)
где С0 – начальная концентрация реагирующего вещества.
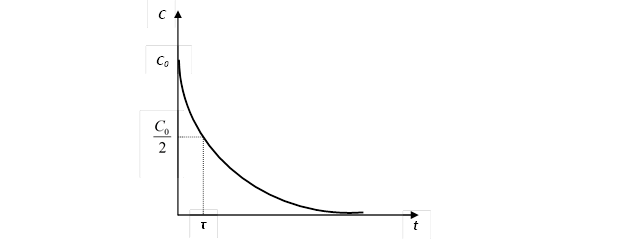
Рис 2. График изменения концентрации вещества, вступающего в реакцию, от времени.
Формула (2) выражает закон химической реакции первого порядка в интегральной форме. Пользуясь уравнением (2), можно определить время, за которое концентрация исходного вещества уменьшается на половину. Это время называют периодом полупревращения или полупериодом протекания реакции и обозначают t.
|
|
|
Подставив значения t=t,  в уравнение (2), получим:
в уравнение (2), получим:
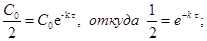

Таким образом, период полупревращения не зависит от исходной концентрации вещества, и за равные промежутки времени расходуется одна и та же доля вещества.
|
|
|


