 |
Теоремы о числовых характеристиках
|
|
|
|
В предыдущем 
мы привели ряд формул, позволяющих находить числовые характеристики функций, когда известны законы распределения аргументов. Однако во многих случаях для нахождения числовых характеристик функций не требуется знать даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики; при этом мы вообще обходимся без каких бы то ни было законов распределения. Определение числовых характеристик функций по заданным числовым характеристикам аргументов широко применяется в теории вероятностей и позволяет значительно упрощать решение ряда задач. По преимуществу такие упрощенные методы относятся к линейным функциям; однако некоторые элементарные нелинейные функции также допускают подобный подход.
В настоящем мы изложим ряд теорем о числовых характеристиках функций, представляющих в своей совокупности весьма простой аппарат вычисления этих характеристик, применимый в широком круге условий.
Математическое ожидание неслучайной величины
Если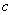 
- неслучайная величина, то
.
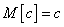Сформулированное свойство является достаточно очевидным; доказать его можно, рассматривая неслучайную величину 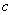как частный вид случайной, при одном возможном значении с вероятностью единица; тогда по общей формуле для математического ожидания:
.
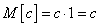Дисперсия неслучайной величины
Если 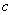- неслучайная величина, то
.
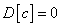Доказательство. По определению дисперсии
.
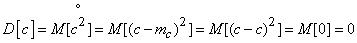Вынесение неслучайной величины за знак математического ожидания
Если 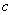- неслучайная величина, а 
- случайная, то
, (10.2.1)
т. е. неслучайную величину можно выносить за знак математического ожидания.
Доказательство.
|
|
|
а) Для прерывных величин
.
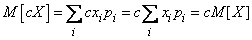б) Для непрерывных величин
.
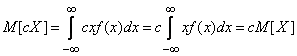Вынесение неслучайной величины за знак дисперсии и среднего квадратического отклонения
Если 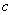- неслучайная величина, а - случайная, то
, (10.2.2)
т. е. неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат.
Доказательство. По определению дисперсии
.
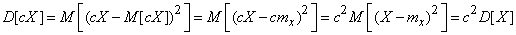Следствие
,
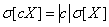т. е. неслучайную величину можно выносить за знак среднего квадратического отклонения ее абсолютным значением. Доказательство получим, извлекая корень квадратный из формулы (10.2.2) и учитывая, что с.к.о. - существенно положительная величина.
Математическое ожидание суммы случайных величин
Докажем, что для любых двух случайных величин и 
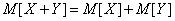, (10.2.3)
т. е. математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
Это свойство известно под названием теоремы сложения математических ожиданий.
Доказательство.
а) Пусть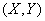 
- система прерывных случайных величин. Применим к сумме случайных величин общую формулу (10.1.6) для математического ожидания функции двух аргументов:
.
Ho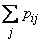 
представляет собой не что иное, как полную вероятность того, что величина примет значение 
:
;
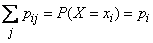следовательно,
.
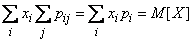Аналогично докажем, что
,
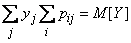и теорема доказана.
б) Пусть 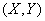- система непрерывных случайных величин. По формуле (10.1.7)
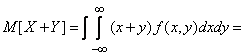
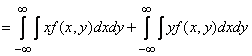. (10.2.4)
Преобразуем первый из интегралов (10.2.4):
;
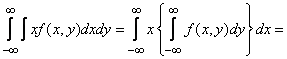
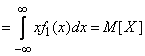аналогично
,
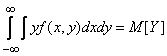и теорема доказана.
Следует специально отметить, что теорема сложения математических ожиданий справедлива для любых случайных величин - как зависимых, так и независимых.
Теорема сложения математических ожиданий обобщается на произвольное число слагаемых:
, (10.2.5)
т. е. математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий.
Для доказательства достаточно применить метод полной индукции.
|
|
|
