 |
Характеристические функции
|
|
|
|
Одна из наиболее общих форм центральной предельной теоремы была доказана А. М. Ляпуновым в 1900 г. Для доказательства этой теоремы А. М. Ляпунов создал специальный метод характеристических функций. В дальнейшем этот метод приобрёл самостоятельное значение и оказался весьма мощным и гибким методом, пригодным для решения самых различных вероятностных задач.
Характеристической функцией случайной величины 
называется функция
, (13.7.1)
где 
- мнимая единица. Функция 
представляет собой математическое ожидание некоторой комплекснойслучайной величины
,
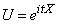функционально связанной с величиной . При решении многих задач теории вероятностей оказывается удобнее пользоваться характеристическими функциями, чем законами распределения.
Зная закон распределения случайной величины , легко найти ее характеристическую функцию.
Если - прерывная случайная величина с рядом распределения
| 
| 
| 
| 
|
| 
| 
|
| 
|
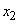
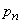
то ее характеристическая функция
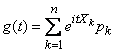(13.7.2)
Если - непрерывная случайная величина с плотностью распределения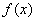 
, то ее характеристическая функция
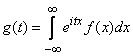. (13.7.3)
Пример 1. Случайная величина - число попаданий при одном выстреле. Вероятность попадания равна 
. Найтихарактеристическую функцию случайной величины .
Решение. По формуле (13.7.2) имеем:
,
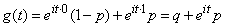где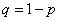 
.
Пример 2. Случайная величина имеет нормальное распределение:
. (13.7.4)
Определить ее характеристическую функцию.
Решение. По формуле (13.7.3) имеем:
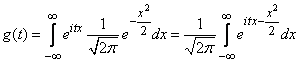. (13.7.5)
Пользуясь известной формулой
и имея в виду, что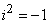 
, получим:
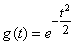. (13.7.6)
Формула (13.7.3) выражает характеристическую функцию непрерывной случайной величины через ее плотность распределения 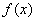. Преобразование (13.7.3), которому нужно подвергнуть 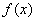, чтобы получить называется преобразованием Фурье. В курсах математического анализа доказывается, что если функция выражается через 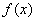с помощью преобразования Фурье, то, в свою очередь, функция 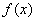выражается через с помощью так называемого обратного преобразования Фурье:
|
|
|
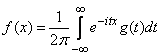. (13.7.7)
Сформулируем и докажем основные свойства характеристических функций.
1. Если случайные величины и 
связаны соотношением
,
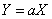где 
- неслучайный множитель, то их характеристические функции связаны соотношением:
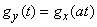. (13.7.8)
Доказательство:
.
2. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.
Доказательство. Даны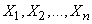 
- независимые случайные величины с характеристическими функциями
и их сумма
.
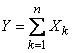Требуется доказать, что
. (13.7.9)
Имеем
.
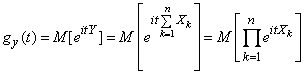Так как величины 
независимы, то независимы и их функции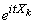 
. По теореме умножения математических ожиданий получим:
,
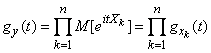что и требовалось доказать.
Аппарат характеристических функций часто применяется для композиции законов распределения. Пусть, например, имеются две независимые случайные величины и с плотностями распределения 
и 
. Требуется найти плотность распределения величины
.
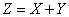Это можно выполнить следующим образом: найти характеристические функци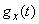и 
и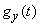 
случайных величин и и, перемножив их, получить характеристическую функцию величины 
:
,
после чего, подвергнув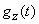 
обратному преобразованию Фурье, найти плотность распределения величины :
.
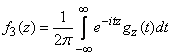Пример 3. Найти с помощью характеристических функций композицию двух нормальных законов:
с характеристиками 
; 
;
с характеристиками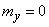 
, 
.
Решение. Находим характеристическую функцию величины . Для этого представим ее в виде
,
где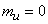 
; 
.
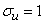Пользуясь результатом примера 2, найдем
.
Согласно свойству 1 характеристических функций,
.
Аналогично
.
Перемножая 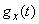и 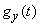, имеем:
,
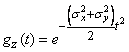а это есть характеристическая функция нормального закона с параметрами 
; 
. Таким образом, получена композиция нормальных законов гораздо более простыми средствами, чем в 
12.6.
|
|
|
|
|
|
