 |
Глава 13 предельные теоремы теории вероятностей
|
|
|
|
Закон больших чисел и центральная предельная теорема
В начале курса мы уже говорили о том, что математические законы теории вероятностей получены абстрагированием реальных статистических закономерностей, свойственных массовым случайным явлениям. Наличие этих закономерностей связано именно с массовостью явлений, то есть с большим числом выполняемых однородных опытов или с большим числом складывающихся случайных воздействий, порождающих в своей совокупности случайную величину, подчиненную вполне определенному закону. Свойство устойчивости массовых случайных явлений известно человечеству еще с глубокой древности. В какой бы области оно ни проявлялось, суть его сводится к следующему: конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате масс и таких явлений; случайные отклонения от среднего, неизбежные в каждом отдельном явлении, в массе взаимно погашаются, нивелируются, выравниваются. Именно эта устойчивость средних и представляет собой физическое содержание «закона больших чисел», понимаемого в широком смысле слова: при очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.
В узком смысле слова под «законом больших чисел» в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.
В 
2.3 мы уже формулировали простейшую из этих теорем - теорему Я. Бернулли. Она утверждает, что при большом числе опытов частота события приближается (точнее - сходится по вероятности) к вероятности этого события. С другими, более общими формами закона больших чисел мы познакомимся в данной главе. Все они устанавливают факт и условия сходимости по вероятности тех или иных случайных величин к постоянным, не случайным величинам.
|
|
|
Закон больших чисел играет важную роль в практических применениях теории вероятностей. Свойство случайных величин при определенных условиях вести себя практически как не случайные позволяет уверенно оперировать с этими величинами, предсказывать результаты массовых случайных явлений почти с полной определенностью.
Возможности таких предсказаний в области массовых случайных явлений еще больше расширяются наличием другой группы предельных теорем, касающихся уже не предельных значений случайных величин, а предельных законов распределения. Речь идет о группе теорем, известных под названием «центральной предельной теоремы». Мы уже говорили о том, что при суммировании достаточно большого числа случайных величин закон распределения суммы неограниченно приближается к нормальному при соблюдении некоторых условий. Эти условия, которые математически можно формулировать различным образом - в более или менее общем виде, - по существу сводятся к требованию, чтобы влияние на сумму отдельных слагаемых было равномерно малым, т. е. чтобы в состав суммы не входили члены, явно преобладающие над совокупностью остальных по своему влиянию на рассеивание суммы. Различные формы центральной предельной теоремы различаются между собой теми условиями, для которых устанавливается это предельное свойство суммы случайных величин.
Различные формы закона больших чисел вместе с различными формами центральной предельной теоремы образуют совокупность так называемых предельных теорем теории вероятностей. Предельные теоремы дают возможность не только осуществлять научные прогнозы в области случайных явлений, но и оценивать точность этих прогнозов.
|
|
|
В данной главе мы рассмотрим только некоторые, наиболее простые формы предельных теорем. Сначала будут рассмотрены теоремы, относящиеся к группе «закона больших чисел», затем - теоремы, относящиеся к группе «центральной предельной теоремы».
Неравенство Чебышева
В качестве леммы, необходимой для доказательства теорем, относящихся к группе «закона больших чисел», мы докажем одно весьма общее неравенство, известное под названием неравенства Чебышева.
Пусть имеется случайная величина 
с математическим ожиданием 
и дисперсией 
. Неравенство Чебышева утверждает, что, каково бы ни было положительное число 
, вероятность того, что величина отклонится от своего математического ожидания не меньше чем на , ограничена сверху величиной 
:
. (13.2.1)
Доказательство. 1. Пусть величина прерывная, с рядом распределения
| 
| 
| 
| 
|
| 
| 
|
| 
|
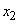
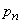
Изобразим возможные значения величины и ее математическое ожидание в виде точек на числовой оси 
(рис. 13.2.1).
Рис. 13.2.1.
Зададимся некоторым значением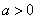 
и вычислим вероятность того, что величина отклонится от своегоматематического ожидания не меньше чем на :
. (13.2.2)
Для этого отложим от точки вправо и влево по отрезку длиной ; получим отрезок 
. Вероятность (13.2.2) есть не что иное, как вероятность того, что случайная точка попадет не внутрь отрезка , а вовне его:
.
Для того чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значений , которые лежат вне отрезка . Это мы запишем следующим образом:
(13.2.3)
где запись 
под знаком суммы означает, что суммирование распространяется на все те значения 
, для которых точки 
, лежат вне отрезка .
С другой стороны, напишем выражение дисперсии величины . По определению:
. (13.2.4)
Так как все члены суммы (13.2.4) неотрицательны, она может только уменьшиться, если мы распространим ее не на все значения , а только на некоторые, в частности на те, которые лежат вне отрезка :
. (13.2.5)
Заменим под знаком суммы выражение 
через . Так как для всех членов суммы , то от такой замены сумма тоже может только уменьшиться; значит,
. (13.2.6)
|
|
|
Но согласно формуле (13.2.3) сумма, стоящая в правой части (13.2.6), есть не что иное, как вероятность попадания случайной точки вовне отрезка ; следовательно,
,
откуда непосредственно вытекает доказываемое неравенство.
2. В случае, когда величина непрерывна, доказательство проводится аналогичным образом с заменой вероятностей элементом вероятности, а конечных сумм - интегралами. Действительно,
. (13.2.7)
где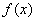 
- плотность распределения величины . Далее, имеем:
,
где знак 
под интегралом означает, что интегрирование распространяется на внешнюю часть отрезка .
Заменяя 
под знаком интеграла через , получим:
,
откуда и вытекает неравенство Чебышева для непрерывных величин.
Пример. Дана случайная величина с математическим ожиданием и дисперсией 
. Оценить сверхувероятность того, что величина отклонится от своего математического ожидания не меньше чем на 
.
Решение. Полагая в неравенстве Чебышева 
, имеем:
,
т. е. вероятность того, что отклонение случайной величины от ее математического ожидания выйдет за пределы трех средних квадратических отклонений, не может быть больше 
.
Примечание. Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. На практике в большинстве случаев вероятность того, что величина выйдет за пределы участка 
, значительно меньше . Например, для нормального закона эта вероятность приблизительно равна 0,003. На практике чаще всего мы имеем дело со случайными величинами, значения которых только крайне редко выходят за пределы . Если закон распределения случайной величины неизвестен, а известны только и 
, на практике обычно считают отрезок участком практически возможных значений случайной величины (так называемое «правило трех сигма»).
|
|
|
