Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения

В главе 7 мы уже рассмотрели некоторые задачи математической статистики, относящиеся к обработке опытных данных. Это были главным образом задачи о нахождении законов распределения случайных величии по результатам опытов. Чтобы найти закон распределения, нужно располагать достаточно обширным статистическим материалом, порядка нескольких сотен опытов (наблюдений). Однако на практике часто приходится иметь дело со статистическим материалом весьма ограниченного объема - с двумя-тремя десятками наблюдении, часто даже меньше. Это обычно связано с дороговизной и сложностью постановки каждого опыта. Такого ограниченного материала явно недостаточно для того, чтобы найти заранее неизвестный закон распределенияслучайной величины; но все же этот материал может быть обработан и использован для получения некоторых сведений о случайной величине. Например, на основе ограниченного статистического материала можно определить - хотя бы ориентировочно - важнейшие числовые характеристики случайной величины: математическое ожидание,дисперсию, иногда - высшие моменты. На практике часто бывает, что вид закона распределения известен заранее, а требуется найти только некоторые параметры, от которых он зависит. Например, если заранее известно, что закон распределения случайной величины нормальный, то задача обработки сводится к определению двух его параметров и . Если заранее известно, что величина распределена по закону Пуассона, то подлежит определению только один его параметр: математическое ожидание . Наконец, в некоторых задачах вид закона распределения вообще несуществен, а требуется знать только его числовые характеристики.

В данной главе мы рассмотрим ряд задач об определении неизвестных параметров, от которых зависит закон распределения случайной величины, но ограниченному числу опытов.

Прежде всего нужно отметить, что любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности. Такое приближенное, случайное значение мы будем называть оценкой параметра. Например, оценкой для математического ожидания может служить среднее арифметическое наблюденных значений случайной величины в независимых опытах. При очень большом числе опытов среднее арифметическое будет с большой вероятностью весьма близко к математическому ожиданию. Если же число опытов невелико, то замена математического ожидания средним арифметическим приводит к какой-то ошибке. Эта ошибка в среднем тем больше, чем меньше число опытов. Так же будет обстоять дело и с оценками других неизвестных параметров. Любая из таких оценок случайна; при пользовании ею неизбежны ошибки. Желательно выбрать такую оценку, чтобы эти ошибки были по возможности минимальными.

Рассмотрим следующую общую задачу. Имеется случайная величина , закон распределения которой содержит неизвестный параметр . Требуется найти подходящую оценку для параметра по результатам независимых опытов, в каждом из которых величина приняла определенное значение.

Обозначим наблюденные значения случайной величины

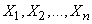. (14.1.1)

Их можно рассматривать как «экземпляров» случайной величины , то есть независимых случайных величин, каждая из которых распределена по тому же закону, что и случайная величина .

Обозначим оценку для параметра . Любая оценка, вычисляемая на основе материала (14.1.1), должна представлять собой функцию величин :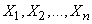

(14.1.2)

и, следовательно, сама является величиной случайной. Закон распределения зависит, во-первых, от закона распределения величины (и, в частности, от самого неизвестного параметра ); во-вторых, от числа опытов . В принципе этот закон распределения может быть найден известными методами теории вероятностей.

Предъявим к оценке ряд требований, которым она должна удовлетворять, чтобы быть в каком-то смысле «доброкачественной» оценкой.

Естественно потребовать от оценки , чтобы при увеличении числа опытов она приближалась (сходилась повероятности) к параметру . Оценка, обладающая таким свойством, называется состоятельной.

Кроме того, желательно, чтобы, пользуясь величиной вместо , мы по крайней мере не делали систематической ошибки в сторону завышения или занижения, т. е. чтобы выполнялось условие

. (14.1.3)

Оценка, удовлетворяющая такому условию, называется несмещенной.

Наконец, желательно, чтобы выбранная несмещенная оценка обладала по сравнению с другими наименьшейдисперсией, т. е.

. (14.1.4)

Оценка, обладающая таким свойством, называется эффективной.

На практике не всегда удается удовлетворить всем этим требованиям. Например, может оказаться, что, даже еслиэффективная оценка существует, формулы для ее вычисления оказываются слишком сложными, и приходится удовлетворяться другой оценкой, дисперсия которой несколько больше. Иногда применяются - в интересах простоты расчетов - незначительно смещенные оценки. Однако выбору оценки всегда должно предшествовать ее критическое рассмотрение со всех перечисленных выше точек зрения.