 |
Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону
|
|
|
|
В предыдущем 
мы рассмотрели грубо приближенные методы построения доверительных интервалов для математического ожидания и дисперсии. В данном мы дадим представление о точных методах решения той же задачи. Подчеркнем, что для точного нахождения доверительных интервалов совершенно необходимо знать заранее вид закона распределения величины 
, тогда как для применения приближенных методов это не обязательно.
Идея точных методов построения доверительных интервалов сводится к следующему. Любойдоверительный интервал находится из условия, выражающего вероятность выполнения некоторых неравенств, в которые входит интересующая нас оценка 
. Закон распределения оценки в общем случае зависит от самих неизвестных параметров величины . Однако иногда удается перейти в неравенствах от случайной величины к какой-либо другой функции наблюденных значений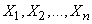 
, закон распределения которой не зависит от неизвестных параметров, а зависит только от числа опытов 
и от вида закона распределения величины . Такого рода случайные величины играют большую роль в математической статистике; они наиболее подробно изучены для случая нормального распределения величины .
Например, доказано, что при нормальном распределении величины случайная величина
, (14.4.1)
где
, 
,
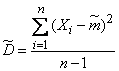подчиняется так называемому закону распределения Стьюдента с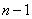 
степенями свободы; плотность этого закона имеет вид
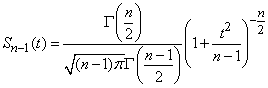, (14.4.2)
где 
- известная гамма-функция:
.
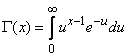Доказано также, что случайная величина
(14.4.3)
имеет «распределение 
» с 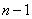степенями свободы (см. гл. 7. стр. 145), плотность которого выражается формулой
(14.4.4)
Не останавливаясь на выводах распределений (14.4.2) и (14.4.4), покажем, как их можно применить при построениидоверительных интервалов для параметров 
и 
.
|
|
|
Пусть произведено независимых опытов над случайной величиной , распределенной по нормальному закону с неизвестными параметрами и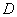 
. Для этих параметров получены оценки
, .
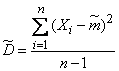Требуется построить доверительные интервалы для обоих параметров, соответствующиедоверительной вероятности 
.
Построим сначала доверительный интервал для математического ожидания. Естественно этот интервал взять симметричным относительно 
; обозначим 
половину длины интервала. Величину нужно выбрать так, чтобы выполнялось условие
. (14.4.5)
Попытаемся перейти в левой части равенства (14.4.5) от случайной величины к случайной величине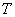 
, распределенной по закону Стьюдента. Для этого умножим обе части неравенства 
на положительную величину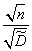 
:
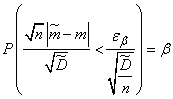
или, пользуясь обозначением (14.4.1),
. (14.4.6)
Найдем такое число 
, что
. (14.4.7)
Величина найдется из условия
. (14.4.8)
Из формулы (14.4.2) видно, что 
- четная функция; поэтому (14.4.8) дает
. (14.4.9)
Равенство (14.4.9) определяет величину в зависимости от . Если иметь в своем распоряжении таблицу значений интеграла
,
то величину можно найти обратным интерполированием в этой таблице. Однако удобнее составить заранее таблицу значений . Такая таблица дается в приложении (см. табл. 5). В этой таблице приведены значения в зависимости от доверительной вероятности и числа степеней свободы 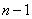. Определив по таблице 5 и полагая
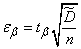, (14.4.10)
мы найдем половину ширины доверительного интервала 
и сам интервал
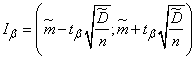. (14.4.11)
Пример 1. Произведено 5 независимых опытов над случайной величиной , распределенной нормально с неизвестными параметрами и 
. Результаты опытов приведены в таблице 14.4.1.
Таблица 14.4.1
| |||||
| -2,5 | 3,4 | -2,0 | 1,0 | 2,1 |
Найти оценку для математического ожидания и построить для него 90%-й доверительный интервал (т. е. интервал, соответствующий доверительной вероятности 
).
|
|
|
Решение. Имеем
; 
.
По таблице 5 приложения для 
и находим
,
откуда
.
Доверительный интервал будет
.
Пример 2. Для условий примера 1 14.3, предполагая величину распределенной нормально, найти точныйдоверительный интервал.
Решение. По таблице 5 приложения находим при 
и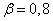 
; отсюда 
.
Сравнивая с решением примера 1 14.3 (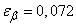
), убеждаемся, что расхождение весьма незначительно. Если сохранить точность до второго знака после запятой, то доверительные интервалы, найденные точным и приближенным методами, совпадают:
.
Перейдем к построению доверительного интервала для дисперсии.
Рассмотрим несмещенную оценку дисперсии
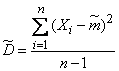
и выразим случайную величину через величину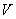 
(14.4.3), имеющую распределение (14.4.4):
. (14.4.12)
Зная закон распределения величины 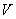, можно найти интервал 
, в который она попадает с заданной вероятностью .
Закон распределения 
величины 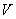имеет вид, изображенный на рис. 14.4.1.
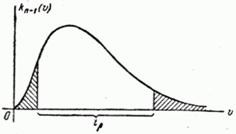
Рис. 14.4.1.
Возникает вопрос: как выбрать интервал ? Если бы закон распределения величины 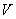был симметричным (как нормальный закон или распределение Стьюдента), естественно было бы взять интервал симметричным относительно математического ожидания. В данном случае закон несимметричен. Условимся выбирать интервал так, чтобы вероятности выхода величины 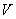за пределы интервала вправо и влево (заштрихованные площади на рис. 14.4.1) были одинаковы и равны
.
Чтобы построить интервал с таким свойством, воспользуемся таблицей 4 приложения: в ней приведены числа такие, что
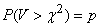
для величины 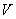, имеющей распределение с 
степенями свободы. В нашем случае 
. Зафиксируем и найдем в соответствующей строке табл. 4 два значения ; одно, отвечающее вероятности 
, другое - вероятности 
. Обозначим эти значения 
и 
. Интервал имеет своим левым, а - правым концом.
Теперь найдем по интервалу искомый доверительный интервал для дисперсии с границами 
и 
, который накрывает точку 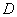с вероятностью :
.
Построим такой интервал 
, который накрывает точку 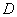тогда и только тогда, когда величина 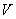попадает в интервал . Покажем, что интервал
(14.4.13)
удовлетворяет этому условию. Действительно, неравенства
; 
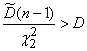
равносильны неравенствам
; 
,
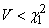а эти неравенства выполняются с вероятностью . Таким образом, доверительный интервал для дисперсии найден и выражается формулой (14.4.13).
|
|
|
Пример 3. Найти доверительный интервал для дисперсии в условиях примера 2 14.3, если известно, что величина распределена нормально.
Решение. Имеем ;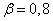 
; 
. По таблице 4 приложения находим при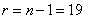 
для 
;
для 
.
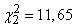По формуле (14.4.13) находим доверительный интервал для дисперсии
.
Соответствующий интервал для среднего квадратического отклонения: 
. Этот интервал лишь незначительно превосходит полученный в примере 2 14.3 приближенным методом интервал 
.
|
|
|
