 |
Оценки для числовых характеристик системы случайных величин
|
|
|
|
В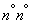 
14.1 - 14.4 мы рассмотрели задачи, связанные с оценками для числовых характеристик однойслучайной величины при ограниченном числе опытов и построением для этих характеристик доверительных интервалов.
Аналогичные вопросы возникают и при обработке ограниченного числа наблюдений над двумя и более случайными величинами.
Здесь мы ограничимся рассмотрением только точечных оценок для характеристик системы.
Рассмотрим сначала случай двух случайных величин.
Имеются результаты 
независимых опытов над системой случайных величин 
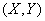, давшие результаты:
; 
; …; 
.
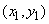Требуется найти оценки для числовых характеристик системы: математических ожиданий 
, дисперсий 
и корреляционного момента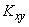 
.
Этот вопрос решается аналогично тому, как мы решили его для одной случайной величины. Несмещенными оценками для математических ожиданий будут средние арифметические:
; 
, (14.6.1)
а для элементов корреляционной матрицы -
(14.6.2)
Доказательство может быть проведено аналогично 
14.2.
При непосредственном вычислении оценок для дисперсий и корреляционного момента часто бывает удобно воспользоваться связью между центральными и начальными статистическими моментами:
(14.6.3)
где
(14.6.4)
Вычислив статистические моменты по формулам (14.6.3), можно затем найти несмещенные оценки для элементовкорреляционной матрицы по формулам:
(14.6.5)
Пример. Произведены стрельбы с самолета по земле одиночными выстрелами. Зарегистрированы координаты точек попадания и одновременно записаны соответствующие значения угла скольжения самолета. Наблюденные значения угла скольжения 
(в тысячных радиана) и абсциссы точки попадания 
(в метрах) приведены в таблице 14.6.1.
Таблица 14.6.1
|
|
|
| 
| 
|
|
|
|
| -8 | -10 | +3 | -1 | ||
| +10 | -2 | -2 | +4 | ||
| +22 | +4 | +28 | +12 | ||
| +55 | +10 | +62 | +20 | ||
| +2 | -1 | -10 | -11 | ||
| -39 | -1+ | -8 | +2 | ||
| -15 | -8 | +22 | +14 | ||
| +5 | -2 | +3 | +6 | ||
| +10 | +6 | -32 | -12 | ||
| +18 | +8 | +8 | +1 |
Найти оценки для числовых характеристик системы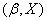 
.
Решение. Для наглядности наносим все пары значений 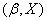на график (рис. 14.6.1). Расположение точек на графике уже свидетельствует о наличии определенной зависимости (положительной корреляции) между .
По формулам (14.6.1) вычисляем средние значения величин и - оценки для математических ожиданий:
; 
.
Рис. 14.6.1.
Далее находим статистические вторые начальные моменты:
;
.
По формулам (14.6.3) находим статистические дисперсии:
;
.
Для нахождения несмещенных оценок умножим статистические дисперсии на 
; получим:
,
.
Соответственно средние квадратические отклонения равны:
; 
.
По последней формуле (14.6.4) находим статистический начальным момент:
и статистический корреляционный момент:
.
Для определения несмещенной оценки умножаем его на ; получаем:
,
откуда оценка для коэффициента корреляции равна:
.
Полученное сравнительно большое значение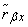 
указывает на наличие существенной связи между и ; на этом основании можно предполагать, что скольжение является основной причиной боковых отклонений снарядов.
Перейдем к случаю обработки наблюдений над системой произвольного числа случайных величин.
Имеется система 
случайных величин
.
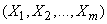Над системой произведено независимых наблюдений; результаты этих наблюдений оформлены в виде таблицы, каждая строка которой содержит значений, принятых случайными величинами 
в одном наблюдении (табл. 14.6.2).
Таблица 14.6.2
|
|
| 
| 
| 
|
| 
|
| 
| 
|
| 
|
| 
|
| 
| 
|
| 
|
| 
|
|
|
|
|
|
|
|
|
| 
| 
|
| 
|
| 
|
|
|
|
|
|
|
|
|
|
| 
| 
|
| 
|
| 
|
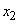
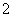
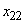
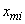
Числа, стоящие в таблице и занумерованные двумя индексами, представляют собой зарегистрированные результаты наблюдений; первый индекс обозначает номер случайной величины, второй - номер наблюдения, так что - это значение, принятое величиной 
в -м наблюдении.
|
|
|
Требуется найти оценки для числовых характеристик системы: математических ожиданий 
и элементов корреляционной матрицы:
.
По главной диагонали корреляционной матрицы, очевидно, стоят дисперсии случайных величин :
; 
; …; 
.
Оценки для математических ожиданий найдутся как средние арифметические:
. (14.6.6)
Несмещенные оценки для дисперсий определятся по формулам
, (14.6.7)
а для корреляционных моментов - по формулам
. (14.6.8)
По этим данным определяются оценки для элементов нормированной корреляционной матрицы:
, (14.6.9)
где
; 
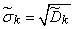. (14.6.10)
Пример. Сброшено 10 серий бомб, по 5 бомб в каждой, и зарегистрированы точки попадания. Результаты опытов сведены в таблицу 14.6.3. В таблице буквой обозначен номер серии; 
- номер бомбы в серии.
Требуется определить подходящие значения числовых характеристик - математических ожиданий и элементовкорреляционных матриц - для системы пяти случайных величин
и системы пяти случайных величин
.
Решение. Оценки для математических ожиданий найдутся как средние арифметические по столбцам:
; 
; 
; 
; 
;
; 
; 
; 
; 
.
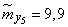При вычислении элементов корреляционной матрицы мы не будем, как в прежних примерах, пользоваться соотношениями между начальными и центральными моментами; в данном случае ввиду сильно изменяющихсяматематических ожиданий пользование этим приемом не даст преимуществ. Будем вычислять оценки для моментов непосредственно по формулам (14.6.2). Для этого вычтем из каждого элемента таблицы 14.6.3 среднее значениесоответствующего столбца. Результаты сведем в таблицу 14.6.4.
Таблица 14.6.3
| Абсцисса X | Абсцисса Y | |||||||||
|
| ||||||||||
| -120 | -20 | -20 | -15 | -8 | -6 | -2 | ||||
| -108 | -75 | -20 | ||||||||
| -200 | -120 | -80 | -20 | -25 | -30 | -20 | -10 | |||
| -55 | -2 | -100 | -75 | -35 | ||||||
| -40 | -30 | -25 | -30 | -45 | ||||||
| -240 | -202 | -140 | -88 | -30 | ||||||
| -40 | -4 | |||||||||
| -100 | -40 | -10 | -70 | -60 | -30 | -10 | ||||
Таблица 14.6.4
|
|
|
| 
| |||||||||
|
| ||||||||||
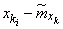
| -45,7 | -0,1 | -25,7 | -25,8 | 33,0 | -16,1 | -13,4 | -20,2 | -19,3 | -11,9 | |
| -33, | -55,1 | -37,7 | -65,8 | -67,0 | 43,9 | 61,6 | 107,8 | 111,7 | 120,1 | |
| -125,7 | -100,1 | -107,7 | -105,8 | -137,0 | -21,1 | -28,4 | -32,2 | -23,3 | -7,9 | |
| 19,3 | 17,9 | 12,3 | 34,2 | 53,0 | -96,1 | -73,4 | -47,2 | -11,3 | -7,9 | |
| 79,3 | 79,9 | 72,3 | 79,2 | 73,0 | -36,1 | -28,4 | -37,2 | -43,3 | -54,9 | |
| -165,7 | -182,1 | -167,7 | -173,8 | -177,0 | 83,9 | 31,6 | 12,8 | -3,3 | -7,9 | |
| 84,3 | 84,9 | 92,3 | 74,2 | 58,0 | 17,9 | 26,6 | 12,8 | 16,7 | 0,1 | |
| 34,3 | 19,9 | 37,3 | 17,2 | 23,0 | 83,9 | 76,6 | 47,8 | -3,3 | -13,9 | |
| -25,7 | -20,1 | -37,7 | -30,8 | -42,0 | -66,1 | -58,4 | -42,2 | -23,3 | -9,9 | |
| 179,3 | 154,9 | 162,3 | 194,2 | 183,0 | 5,9 | 5,6 | -2,2 | -1,3 | -5,9 |
Возводя эти числа в квадрат, суммируя по столбцам и деля на 
, получим оценки для дисперсий и средних квадратических отклонений:
; 
; 
;
; 
;
; 
; 
; 
; 
.
; 
; 
;
; 
;
; 
; 
; 
; 
.
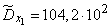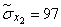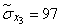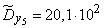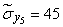Чтобы найти оценку для корреляционного момента, например, между величинам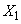и 
и 
составим столбец попарных произведении чисел, стоящих в первом и втором столбцах таблицы 14.6.4. Сложив все эти произведения и разделив сумму на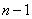 
, получим:
.
Деля 
на 
получим:
.
Аналогично находим все остальные элементы корреляционных матриц. Для удобства умножим все элементы обеих матриц моментов на 
. Получим:
.
(Ввиду симметричности матриц они заполнены только наполовину.)
Нормированные корреляционные матрицы имеют вид:
.
Рассматривая эти матрицы, убеждаемся, что величины находятся в весьма тесной зависимости, приближающейся к функциональной; величины связаны менее тесно, и коэффициенты корреляциимежду ними убывают по мере удаления от главной диагонали корреляционной матрицы.
Обработка стрельб
Одной из важных практических задач, возникающих при изучении вопросов стрельбы и бомбометания, является задача обработки результатов экспериментальных стрельб (бомбометаний).
Здесь мы будем различать два случая: стрельбу ударными снарядами и стрельбу дистанционными снарядами.
При стрельбе ударными снарядами рассеивание характеризуется законом распределения системы двух случайных величин: абсциссы и ординаты точки попадания на некоторой плоскости (реальной или воображаемой). При стрельбе дистанционными снарядами рассеивание носит пространственный характер и описывается законом распределения системы трех координат точки разрыва снаряда.
|
|
|
Рассмотрим сначала задачу обработки стрельб ударными снарядами. Пусть произведено независимых выстрелов по некоторой плоской мишени и зарегистрированы координаты точек попадания (рис. 14.7.1):
.
Рис. 14.7.1.
Предполагая, что закон распределения системы 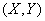нормальный, требуется найти оценки для его параметров: координат центра рассеивания 
, 
, угла 
, определяющего направление главных осей рассеивания 
, 
и главных с.к.о. 
, 
.
Начнем с рассмотрения самого простого случая, когда направление главных осей рассеивания известно заранее. Этот случай часто встречается на практике, так как обычно направление главных осей рассеивания определяется самими условиями стрельбы (например, при бомбометании - направление полета и перпендикулярное к нему; при воздушной стрельбе - направление поперечной скорости цели и перпендикулярное к нему и т. д.). В этом случае задача обработки стрельб сильно упрощается. Зная заранее хотя бы ориентировочно направление главных осей, можно выбрать координатные оси параллельно им; в такой системе координат абсцисса и ордината точки попадания представляют собой независимые случайные величины, и их закон распределения определяется всего четырьмя параметрами: координатами центра рассеивания и главными средними квадратическими отклонениями 
, 
. Оценки для этих параметров определяются формулами
(14.7.1)
Рассмотрим более сложный случай, когда направление главных осей рассеивания заранее неизвестно и тоже должно быть определено из опыта. В этом случае определению подлежат оценки всех пяти параметров: координат центра рассеивания , , угла и главных средних квадратических отклонений , (рис. 14.7.2).
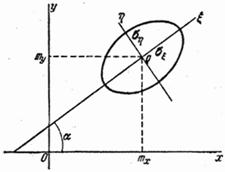
Рис. 14.7.2.
Оценки для координат центра рассеивания в этом случае определяются так же, как в предыдущем случае, по формулам
; . (14.7.2)
Перейдем к оценке угла . Предположим, что направления главных осей рассеивания известны, и проведем через точку 
главные оси 
, 
(рис. 14.7.2). В системе 
координаты случайной точки 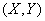будут:
или
(14.7.3)
Очевидно, величины 
будут иметь математические ожидания, равные нулю:
.
Так как оси , - главные оси рассеивания, величины независимы. Но для величин, подчиненных нормальному закону, независимость эквивалентна некоррелированности; следовательно, нам достаточно найти такое значение угла , при котором величины не коррелированы. Это значение и определит направление главных осей рассеивания.
Вычислим корреляционный момент величин 
. Перемножая равенства (14.7.3) и применяя к их произведению операцию математического ожидания, получим:
|
|
|
.
Приравнивая это выражение нулю и деля обе части на 
, имеем:
. (14.7.4)
Уравнение (14.7.4) даст два значения угла : 
и 
, различающиеся на 
. Эти два угла и определяют направления главных осей рассеивания.
Заменяя в равенстве (14.7.4) ,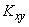 
, 
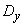их оценками, получим оценку для угла :
.
Найдем оценки для главных средних квадратических отклонений , . Для этого найдем дисперсии величин , заданных формулами (14.7.3), по теореме о дисперсии линейной функции:
;
,
откуда находим оценки для главных дисперсий:
(14.7.5)
Оценки для главных средних квадратических отклонений выразятся формулами:
(14.7.6)
Выпишем отдельно полную сводку формул для обработки стрельб по плоской мишени в случае, когда направление главных осей рассеивания заранее неизвестно. Оценки искомых параметров определяются формулами:
(14.7.7)
где
(14.7.8)
В заключение следует заметить, что обработку стрельб по полным формулам (14.7.7) имеет смысл предпринимать только тогда, когда число опытов достаточно велико (порядка многих десятков; только в этом случае угол может быть оценен с достаточном точностью. При малом числе наблюдений значение 
, полученное обработкой, является в значительной мере случайным.
Задачу обработки стрельб дистанционными снарядами мы здесь рассмотрим только в простейшем случае, когда направление главных осей рассеивания (хотя бы ориентировочно) известно заранее. Как правило, встречающиеся в практике стрельбы дистанционными снарядами задачи обработки опытов относятся к этому типу. Тогда можно выбрать координатные оси параллельно главным осям рассеивания и рассматривать три координаты точки разрыва снаряда как независимые случайные величины.
Пусть в результате независимых выстрелов зарегистрированы координаты точек разрыва дистанционных снарядов
в системе координат с осями, параллельными главным осям рассеивания. Оценки для параметров нормального закона определятся формулами:
(14.7.9)
На решении задачи обработки стрельб дистанционными снарядами в случае, когда направления главных осей рассеивания заранее неизвестны, мы останавливаться не будем, так как на практике эта задача встречается сравнительно редко.
|
|
|
