Преобразование стационарной случайной функции стационарной линейной системой

В главе 16 мы познакомились с общими правилами линейных преобразований случайных функций, представленных в виде канонических разложений. Эти правила сводятся к тому, что при линейных преобразованиях случайных функций их математические ожидания и координатные функции подвергаются тем же линейным преобразованиям. Таким образом, задача линейного преобразования случайной функции сводится к задаче такого желинейного преобразования нескольких неслучайных функций.

В случае, когда речь идет о линейных преобразованиях стационарных случайных функций, задачу удается упростить еще больше.

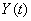Если и входное воздействие и реакция системы стационарны, задачу преобразования случайной функцииможно свести к преобразованию одной-единственной неслучайной функции - спектральной плотности .

Для того чтобы при стационарном воздействии реакция системы могла быть тоже стационарной, очевидно необходимо, чтобы параметры системы (например, входящие в нее сопротивления, емкости, индуктивности и т. п.) были постоянными, а не переменными. Условимся называть линейную систему с постоянными параметрами стационарной линейной системой. Обычно работа стационарной линейной системы описывается линейными дифференциальными уравнениями с постоянными коэффициентами.

Рассмотрим задачу о преобразовании стационарной случайной функции стационарной линейной системой. Пусть на вход линейной системы 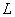поступает стационарная случайная функция ; реакция системы есть случайная функция 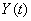рис. (17.5.1).

Рис. 17.5.1.

Известны характеристики случайной функции : математическое ожидание и корреляционная функция 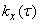. Требуется определить характеристики случайной функции 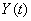на выходе линейной системы.

Так как для решения задачи нам придется преобразовывать неслучайные функции - математическое ожидание и координатные функции, рассмотрим прежде всего задачу об определении реакции системы 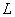на неслучайное воздействие .

Напишем в операторной форме линейное дифференциальное уравнение с постоянными коэффициентами, связывающее реакцию системы с воздействием :

. (17.5.1)

где - оператор дифференцирования.

Уравнение (17.5.1) короче можно записать в виде:

, (17.5.2)

или, наконец, условно разрешая уравнение (17.5.2) относительно , записать оператор системы в «явном» виде:

. (17.5.3)

Реакцию системы 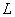на воздействие можно найти путем решения линейного дифференциального уравнения(17.5.1). Как известно из теории дифференциальных уравнений, это решение состоит из двух слагаемых: и . Слагаемое представляет собой решение уравнения без правой части и определяет так называемые свободные или собственные колебания системы. Это - колебания, совершаемые системой при отсутствии входного воздействия, если система в начальный момент как-то была выведена из состояния равновесия. На практике чаше всего встречаются так называемые устойчивые системы; в этих системах свободные колебания с течением времени затухают.

Если ограничиться рассмотрением участков времени, достаточно удаленных от начала процесса, когда все переходные процессы в системе можно считать законченными, и система работает в установившемся режиме, можно отбросить второе слагаемое и ограничиться рассмотрением только первого слагаемого . Это первое слагаемое определяет так называемые вынужденные колебания системы под влиянием воздействия на нее заданной функции .

В случае, когда воздействие представляет собой достаточно простую аналитическую функцию, часто удается найти реакцию системы также в виде простой аналитической функции. В частности, когда воздействие представляет собой гармоническое колебание определенной частоты, система отвечает на него также гармоническим колебанием той же частоты, но измененным по амплитуде и фазе.

Так как координатные функции спектрального разложения стационарной случайной функции представляют собой гармонические колебания, то нам прежде всего необходимо научиться определять реакцию системы на гармоническое колебание заданной частоты . Эта задача решается очень просто, особенно еслигармоническое колебание представлено в комплексной форме.

Пусть на вход системы поступает гармоническое колебание вида:

. (17.5.4)

Будем искать реакцию системы также в виде гармонического колебания частоты , но умноженного на некоторый комплексный умножитель :

. (17.5.5)

Множитель найдем следующим образом. Подставим функцию (17.5.4) в правую, а функцию (17.5.5) в левую часть уравнения (17.5.1). Получим:

. (17.5.6)

Имея в виду, что при любом

, ,

и деля обе части уравнения (17.5.6) на , получим:

. (17.5.7)

Мы видим, что множитель при представляет собой не что иное, как многочлен , в который вместо оператора дифференцирования подставлено ; аналогично правая часть равенства (17.5.7) есть не что иное, как . Уравнение (17.5.7) можно записать в виде:

,

откуда

. (17.5.8)

Функция носит специальное название частотной характеристики линейной системы. Для определениячастотной характеристики достаточно в оператор системы, записанный в явной форме (17.5.3), вместо оператора дифференцирования подставить .

Таким образом, если на вход линейной системы с постоянными параметрами поступает гармоническое колебаниевида , то реакция системы представляется в виде того же гармонического колебания, умноженного начастотную характеристику системы . Пусть на вход системы поступает воздействие вида

, (17.5.9)

где - некоторая величина, не зависящая от . В силу линейности системы величина выходит за знак оператора, и реакция системы на воздействие (17.5.9) будет равна:

. (17.5.10)

Очевидно, это свойство сохранится и в том случае, когда величина будет случайной (лишь бы она не зависела от ).

Применим изложенные приемы преобразования гармонических колебаний линейной системой к математическому ожиданию случайной функции и координатным функциям ее спектрального разложения.

Представим математическое ожидание стационарной случайной функции как гармоническое колебаниенулевой частоты и положим в формуле (17.5.8) :

, (17.5.11)

откуда получаем математическое ожидание на выходе системы:

. (17.5.12)

Перейдем к преобразованию линейной системой существенно случайной части функции , а именно функции

. (17.5.13)

Для этого представим функцию на участке в виде спектрального разложения:

, (17.5.14)

где 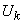- некоррелированные случайные величины, дисперсии которых образуют спектр случайной функции .

Рассмотрим отдельное слагаемое этой суммы:

. (17.5.15)

Реакция системы на это воздействие будет иметь вид:

. (17.5.16)

Согласно принципу суперпозиции реакция системы на сумму воздействия равна сумме реакций на отдельные воздействия. Следовательно, реакцию системы на воздействие (17.5.14) можно представить в виде спектрального разложения:

,

или, обозначая ,

, (17.5.17)

где - некоррелированные случайные величины с математическими ожиданиями, равными нулю.

Определим спектр этого разложения, Для этого найдем дисперсию комплексной случайной величины в разложении (17.5.17). Имея в виду, что дисперсия комплексной случайной величины равна математическому ожиданию квадрата ее модуля, имеем:

. (17.5.18)

Мы приходим к следующему выводу: при преобразовании стационарной случайной функции стационарнойлинейной системой каждая из ординат ее спектра умножается на квадрат модуля частотной характеристикисистемы для соответствующей частоты.

Таким образом, при прохождении стационарной случайной функции через линейную стационарную систему ее спектр определенным образом перестраивается: некоторые частоты усиливаются, некоторые, напротив, ослабляются (фильтруются). Квадрат модуля частотной характеристики (в зависимости от ) и показывает, как реагирует система на колебания той или иной частоты.

Аналогично тому, как это делалось раньше, перейдем в спектральном представлении случайной функции к пределу при и от дискретного спектра - к спектральной плотности. Очевидно, спектральная плотность на выходелинейной системы получается из спектральной плотности на входе тем же умножением на , как и ординаты дискретного спектра:

. (17.5.19)

Таким образом, получено весьма простое правило:

При преобразовании стационарной случайной функции стационарной линейной системой ееспектральная плотность умножается на квадрат модуля частотной характеристики системы.

Пользуясь этим правилом, мы легко можем решить поставленную выше задачу: по характеристикам случайной функции на входе линейной системы найти характеристики случайной функции на ее выходе.

Пусть на вход стационарной линейной системы с оператором (17.5.3) поступает стационарная случайная функция с математическим ожиданием и корреляционной функцией 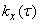. Требуется найтиматематическое ожидание и корреляционную функцию случайной функции 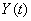на выходе системы.

Задачу будем решать в следующем порядке.

1. Находим математическое ожидание на выходе:

. (17.5.20)

2. По корреляционной функции 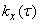находим спектральную плотность на входе (см. формулу (17.4.12)):

. (17.5.21)

3. По формуле (17.5.8) находим частотную характеристику системы и квадрат ее модуля:

. (17.5.22)

4. Умножая спектральную плотность на входе на квадрат модуля частотной характеристики, находим спектральную плотность на выходе:

. (17.5.23)

5. По спектральной плотности находим корреляционную функцию на выходе системы:

. (17.5.24)

Таким образом, поставленная задача решена.

Во многих задачах практики нас интересует не вся корреляционная функция на выходе системы, а толькодисперсия 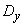, равная

.

Тогда из формулы (17.5.24) получаем при гораздо более простую формулу:

,

или, учитывая четность функции ,

. (17.5.25)

Пример. Работа линейной динамической системы описывается линейным дифференциальным уравнением первого порядка:

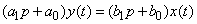, (17.5.26)

или

.

На вход системы поступает стационарная случайная функция с математическим ожиданием и корреляционной функцией

, (17.5.27)

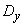где - положительный коэффициент (см. пример 1 17.4). Найти математическое ожидание и дисперсию на выходе системы.

Решение. По формуле (17.5.20) имеем:

.

Очевидно, величина не зависит от параметра , растет при возрастании и убывает при возрастании .

Спектральную плотность на входе определяем как в примере 1 17.4:

(см. рис. 17.4.4).

По формуле (17.5.8) находим частотную характеристику системы:

и квадрат ее модуля:

.

Затем определяем спектральную плотность на выходе системы:

.

Далее по формуле (17.5.25) определяем дисперсию на выходе:

.

Для вычисления интеграла разложим подынтегральное выражение на простые дроби:

и определим коэффициенты:

;

.

После интегрирования получим:

.

В заключение данного упомянем о том, как преобразуется линейной системой стационарная случайная функция, содержащая в качестве слагаемого обычную случайную величину:

, (17.5.28)

где - случайная величина с дисперсией , - стационарная случайная функция.

Реакция системы на воздействие 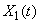) найдется как сумма реакций на отдельные воздействия в правой части (17.5.28). Реакцию на воздействие мы уже умеем находить. Воздействие мы рассмотрим какгармоническое колебание нулевой частоты ; согласно формуле (17.5.11) реакция на него будет равна

. (17.5.29)

Слагаемое просто прибавится к реакции системы на воздействие .

 

⇐ Предыдущая67686970717273747576Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: