 |
Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий
|
|
|
|
На двух примерах, приведенных в предыдущем 
, мы наглядно убедились в том, что существует связь между характером корреляционной функции и внутренней структурой соответствующего ей случайного процесса. В зависимости от того, какие частоты и в каких соотношениях преобладают в составе случайной функции, еекорреляционная функция имеет тот или другой вид. Из таких соображений мы непосредственно приходим к понятию о спектральном составе случайной функции.
Понятие «спектра» встречается не только в теории случайных функций; оно широко применяется в математике, физике и технике.
Если какой-либо колебательный процесс представляется в виде суммы гармонических колебаний различных частот (так называемых «гармоник»), то спектром колебательного процесса называется функция, описывающая распределение амплитуд по различным частотам. Спектр показывает, какого рода колебания преобладают в данном процессе, какова его внутренняя структура.
Совершенно аналогичное спектральное описание можно дать и стационарному случайному процессу; вся разница в том, что для случайного процесса амплитуды колебаний будут случайными величинами. Спектр стационарнойслучайной функции будет описывать распределение дисперсий по различным частотам.
Подойдем к понятию о спектре стационарной случайной функции из следующих соображений.
Рассмотрим стационарную случайную функцию 
, которую мы наблюдаем на интервале 
(рис. 17.2.1).
Рис. 17.2.1.
Задана корреляционная функция случайной функции 
.
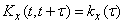Функция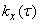 
есть четная функция:
и, следовательно, на графике изобразится симметричной кривой (рис. 17.2.2).
Рис. 17.2.2.
При изменении 
и 
от 
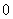до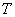 
аргумент 
изменяется от 
до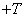 
.
|
|
|
Мы знаем, что четную функцию на интервале 
можно разложить в ряд Фурье, пользуясь только четными (косинусными) гармониками:
, (17.2.1)
где
; 
, (17.2.2)
а коэффициенты 
определяются формулами:
(17.2.3)
Имея в виду, что функци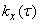и и 
четные, можно преобразовать формулы (17.2.3) к виду:
(17.2.4)
Перейдем в выражении (17.2.1) корреляционной функции 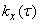от аргумента 
снова к двум аргументам и . Для этого положим
(17.2.5)
и подставим выражение (17.2.5) в формулу (17.2.1):
. (17.2.6)
Мы видим, что выражение (17.2.6) есть не что иное, как каноническое разложение корреляционной функции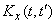 
. Координатными функциями этого канонического разложения являются попеременно косинусы и синусы частот, кратных 
:
.
Мы знаем, что по каноническому разложению корреляционной функции можно построить каноническое разложение самой случайной функции с теми же координатными функциями и с дисперсиями, равными коэффициентам в каноническом разложении корреляционной функции.
Следовательно, случайная функция может быть представлена в виде канонического разложения:
, (17.2.7)
где 
- некоррелированные случайные величины с математическими ожиданиями, равными нулю, и дисперсиями, одинаковыми для каждой пары случайных величин с одним и тем же индексом 
:
. (17.2.8)
Дисперсии при различных определяются формулами (17.2.4).
Таким образом, мы получили на интервале каноническое разложение случайной функции , координатными функциями которого являются функции 
, 
при различных 
. Разложение такого рода называется спектральным разложением стационарной случайной функции. На представлениислучайных функций в виде спектральных разложений основана так называемая спектральная теория стационарныхслучайных процессов.
Спектральное разложение изображает стационарную случайную функцию разложенной на гармонические колебания различных частот:
причем амплитуды этих колебаний являются случайными величинами.
|
|
|
Определим дисперсию случайной функции , заданной спектральным разложением (17.2.7). По теореме о дисперсии линейной функции некоррелированных случайных величин
. (17.2.9)
Таким образом, дисперсия стационарной случайной функции равна сумме дисперсий всех гармоник ее спектрального разложения. Формула (17.2.9) показывает, что дисперсия функции известным образом распределена по различным частотам: одним частотам соответствуют большие дисперсии, другим - меньшие. Распределение дисперсий по частотам можно проиллюстрировать графически в виде так называемого спектра стационарной случайной функции (точнее - спектра дисперсий). Для этого по оси абсцисс откладываются частоты 
, а по оси ординат - соответствующие дисперсии (рис. 17.2.3).
Рис. 17.2.3.
Очевидно, сумма всех ординат построенного таким образом спектра равна дисперсии случайной функции.
|
|
|
