 |
С о в м е с т и м о с т ь. Несовместимость
|
|
|
|
С о в м е с т и м о с т ь
1. Подчинение.
Подчинение характеризует отношения между А и I, Е и О, причем частные суждения подчиняются общим.
А(Е) назовем подчиняющим суждением, I (О) - подчиненным суждением.
а) Истинность подчиняющего суждения обусловливает истинность подчиненного, т. е. если суждение " Все великие люди низкого роста" (А) истинно, то истинно и суждение " Некоторые великие люди низкого роста" (I). То же для Е и О.
б) Ложность подчиненного суждения обусловливает ложность подчиняющего суждения. Если суждение " Некоторые эпузы гантируются" (I) ложно, то суждение " Все эпузы гантируются" (A) также ложно. То же для О и Е.
в) Вместе с тем подчиняющее и подчиненное суждения могут быть вместе ложны. Так, суждения " Ни один человек не является смертным" (E) и " Некоторые люди не являются смертными" (O) одновременно ложны.
Если для обозначения отношения подчинения ввести знак " ╞ ", то указанные отношения будут выглядеть следующим образом:
A╞ I
Е╞ О
2. Дополнительность [45] .
Дополнительность характеризует отношения между I и О.
Суждения находятся в отношении дополнительности, если они не могут быть вместе ложными.
Отсюда вытекает:
а) они могут быть вместе истинными;
б, в) одно из них может быть истинным, а другое - ложным.
Пример. Рассмотрим суждения " Некоторые студенты являются веселыми людьми" и " Некоторые студенты не являются веселыми людьми" . Очевидно, что они могут быть вместе истинными. Но мобут ли они быть вместе ложными? Предположим, что суждение " Некоторые студенты являются веселыми людьми" ложно. Это означает, что среди студентов нет ни одного веселого человека, т. е. суждение " Ни один студент не является веселым человеком" истинно, тогда в силу отношения подчинения суждение " Некоторые студенты не являются веселыми людьми" будет истинным, и следовательно, не может быть ложным.
|
|
|
Дополнительность характеризует отношения между I и О следующим образом.
Если I ложно, то О истинно.
Если О ложно, то I истинно.
Несовместимость
1. Противоречие.
Суждения находятся в отношении противоречия, если они не могут быть ни вместе истинны, ни вместе ложны.
В отношении противоречия находятся суждения А и О, Е и I.
Пример. Именно отношение противоречия помогло нашим героям найти наилучшую стратегию в споре. Суждения " Все великие люди имеют низкий рост" и суждение " Некоторые великие люди не являются людьми низкого роста" находятся в отношении противоречия. Если одно из них истинно, то другое обязательно ложно, и наоборот.
Противоречие можно охарактеризовать следующим образом.
Если А (Е) истинно, то О (I) ложно.
Если А (Е) ложно, то О (I) истинно.
Если О (I) истинно, то А (Е) ложно.
Если О (I) ложно, то А (Е) истинно.
Нетрудно заметить, сколь содержательно отношение противоречия, сколько конкретных отношений между отдельными видами категорических суждений вытекает из этого отношения.
Отношение противоречия - одно из самых важных видов логических отношений вообще. Вы могли убедиться в этом, когда мы решали задачи о рыцарях и лжецах, или когда вы использовали метод доказательства от противного при решении математических задач. Обратите внимание на то, что нам удавалось добиться прогресса в решении задачи, когда мы обнаруживали противоречие между суждениями и устраняли его.
Заметим, что каждое логически истинное суждение находится в отношении противоречия с каждым логически ложным суждением.
|
|
|
2. Противоположность.
Суждения А и В находятся в отношении противоположности, если они не могут быть вместе истинными.
Очевидно, что мни могут быть вместе ложными. В отношении противоположности находятся суждения А и Е. Между ними имеются следующие отношения:
Если А истинно, то Е ложно,
Если Е истинно, то А ложно.
Пример. Суждения " Все великие люди - низкого роста" и " Ни один великий человек не является человеком низкого роста" находятся в отношении противоположности.
" Ав: Подведем итоги. Пусть наш оппонент в споре выдвигает суждение " Все интеллигенты - бездельники" . Как мы с ним будем спорить?
Ст: Здесь велик соблазн броситься защищать мнение " Ни один интеллигент не является бездельником" . Но теперь мы знаем, что это не лучшая стратегия, если ты хочешь выиграть спор.
Сс: Правильно. Теперь ясно, что следует пользоваться отношением противоречия, потому что именно суждение, находящееся в отношении противоречия, является наиболее полным отрицанием того, что сказано в исходном суждении. Если нам удастся обосновать противоречащее суждение, то из этого определенно следует ложность суждения нашего оппонента.
Ав: А почему неправильно пользоваться отношением противоположности?
Сс: Потому что в этом случае мы, хотя и смогли бы доказать ложность убеждения оппонента, но нам пришлось бы доказывать слишком много.
Ст: Итак, мы будем доказывать суждение " Некоторые интеллигенты не являются бездельниками" . Вот мы, например, уже сколько времени непрерывно заняты делом, ибо разве может быть лучшее дело для интеллигента, чем совершенствовать свое мышление.
Ав: Мыслить самостоятельно и правильно - важнейшее дело. Иммануил Кант говорил, что это - свойство просвещенного мышления. Что ж, будем мыслить просвещенно. "
Итак, в результате рассмотрения отношений между категорическими суждениями получилась следующая классификация:
§ 2. Отношения между сложными суждениями
Сложные суждения вступают в отношения, подобные отношениям между категорическими суждениями, которые мы систематизировали при помощи логического квадрата. Однако имеются и некоторые отличия.
|
|
|
Начнем мы также с отношений сравнимости и несравнимости.
Для начала введем некоторые дополнительные понятия. Отношения между сложными суждениями, допустим А и В, мы будем выяснять при помощи построенной для них совместной таблицы истинности.
Совместная таблица для суждений А и В строится следующим образом:
Вход таблицы строим как для суждения 
, т. е. на входе выписываем объединение множества простых суждений из А и В, а затем вычисляем истинностные значения суждений А и В отдельно.
Пример. Рассмотрим суждения 
и 
.
Объединением множества простых суждений из А и В будет {p, q, r}. Следовательно, строим вход таблицы с тремя простыми суждениями, а далее вычисляем истинностные значения А и В по отдельности[46].
| p | q | r | 
| 
| 
| 
|
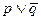
| И | И | И | Л | И | Л | Л |
| И | И | Л | Л | И | Л | Л |
| И | Л | И | И | И | Л | Л |
| И | Л | Л | И | И | Л | Л |
| Л | И | И | Л | Л | И | И |
| Л | И | Л | Л | Л | И | Л |
| Л | Л | И | И | И | И | И |
| Л | Л | Л | И | И | И | Л |
Мы видим, что в совместной таблице возможны различные сочетания истинностных значений сложных суждений А и В. В общем случае (И И), (И Л), (Л И), (Л Л) - все возможные комбинации значений истинности двух суждений.
Сложные суждения А и В назовем несравнимыми, если в совместно построенной для них таблице среди сочетаний их истинностных значений встречаются все возможные комбинации.
Пример. Суждения 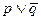и являются несравнимыми, поскольку в совместной таблице встречаются все возможные комбинации истинностных значений. См. строки 4, 5, 6, 7.
Сложные суждения А и В назовем сравнимыми, если в совместной таблице среди сочетаний их истинностных значений отсутствует хотя бы одна возможная комбинация.
Пример. Суждения 
и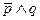 
сравнимы, потому что в совместной таблице отсутствует комбинация истинностных значений (Л И).
Проверьте это сами.
Среди сравнимых суждений мы будем различать совместимые и несовместимые суждения.
Совместимыми назовем суждения, одновременно истинные или принимающие во всех строках таблицы одни и те же значения.
|
|
|
Несовместимыми назовем суждения, которые не являются одновременно истинными и не принимают во всех строках таблицы одни и те же значения.
Вопрос о том, могут или не могут данные суждения быть одновременно истинными (ложными), решается при помощи таблиц истинности. Теперь мы можем уточнить, что значит быть одновременно истинными (ложными).
Суждения А и В одновременно истинны (ложны), если они принимают значения И (Л) в одной и той же строке, построенной для них совместно таблицы.
|
|
|
