Несовместимость

Отношение несовместимости сводится к двум типам: а) противоречию и б) противоположности.

а) Противоречие

Рассмотрим ситуацию спора. Ваш оппонент придерживается мнения о том, что " Наполеон - великий человек, и прекрасно все то, что он совершил". Вам необходимо опровергнуть Вашего оппонента. Какое же суждение вам следует доказать, чтобы Ваш оппонент был опровергнут по всем пунктам? Пойдет ли такое: " Наполеон - не великий человек, и не является прекрасным все то, что он совершил". Возможно, что этого достаточно для опровержения Вашего оппонента. Но так ли легко это доказать, особенно ту часть, что Наполеон - не великий человек? Чтобы ответить на этот вопрос, нам надо рассмотреть отношение противоречия, ибо точное отрицание некоторого суждения как раз и дает нам отношение противоречия.

Суждения А и В находятся в отношении противоречия, если они не могут быть ни вместе истинными, ни вместе ложными.

Нам осталось выяснить, какое же суждение будет находиться к суждению Аашего оппонента в отношении противоречия. Проверим то суждение, которое было предложено выше. Обозначим " Наполеон - великий человек" через p, а " Прекрасно все то, что он совершил" через q. Тогда первое суждение запишем как , второе – как .

Построим таблицу.

 

p	q
И	И		И	Л
И	Л		Л	Л
Л	И		Л	Л
Л	Л		Л	И

 

Как мы видим, эти суждения не могут быть вместе истинными, но могут быть вместе ложными. Отсюда и возникает впечатление того, что такое суждение требует от нас слишком много. Попробуем суждение формы .

 

p	q
И	И		И	Л
И	Л		Л	И
Л	И		Л	И
Л	Л		Л	И

 

Мы видим, что суждение  находится с суждением   в отношении противоречия. Поэтому в нашем споре следует придерживаться следующей стратегии - выдвинуть в противовес нашему сопернику суждение " Наполеон - не великий человек, или не прекрасно все то, что он совершил". Это суждение доказать уже намного легче, поскольку для этого достаточно доказать, что не все, что сделал Наполеон, прекрасно.

Таким образом, мы с вами убедились в следующем положении:

Выбирая оптимальную стратегию спора, следует руководствоваться отношением противоречия.

Отношение противоречия - важнейшее отношение в логике, сравнимое по своему значению только с отношением логического следования. Рассматривая таблицу, характеризующую отношение противоречивых суждений, мы можем установить такую закономерность: если суждение А находится в отношении противоречия к суждению B, то B представляет собой отрицание А, т. е. , а .

Пояснение. Каждое логически истинное суждение находится в отношении противоречия к каждому логически ложному.

б) Противоположность

Иногда возникает задача обнаружения суждения не только исключающего истинность данного суждения, но и утверждающего нечто сверх этого. В таком случае можно прибегнуть к отношению противоположности.

Суждения А и В находятся в отношении противоположности, если в построенной для них совместно таблице не встречается комбинации значений (И И), но встречаются все остальные возможные комбинации.

Пример. Когда мы искали суждение, находящееся в отношении противоречия к , то рассматривали случай . Это был случай отношения противоположности. Взгляд на таблицу покажет Вам, что эти суждения могут быть вместе ложными, но не могут быть вместе истинными.

В результате мы имеем следующую кйассификацию отношений между сложными суждениями.

 

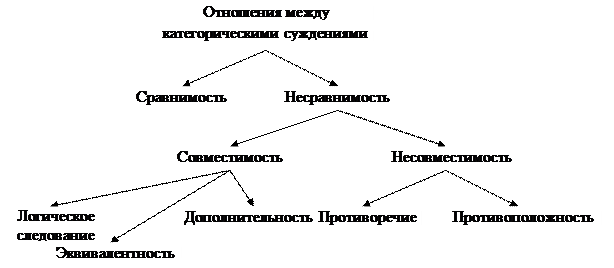
Рис. 3

Общее замечание. Навык обращения с различными отношениями между суждениями позволяет нам в общении, например, в споре легко находить суждения, следующие из данных, суждения, противоречащие им, и т. д. А это необходимо для развития аргументов в пользу своего тезиса и критики чужих тезисов и аргументов.

 

ГЛАВА 8

ЗАКОНЫ ЛОГИКИ

 

 

§ 1. Общая характеристика

 

В логике XX века ствердился взгляд, согласно которому закон логики описывает такие связи между суждениями, при которых получающееся сложное суждение истинно независимо от того, о чем говорят сами эти суждения: о столах, стульях, электронах, доброте, самопожертвовании, импрессионизме и т. п. Это положение можно выразить еще и следующим образом:

 

Законы логики — это такие суждения, которые являются истинными только в силу своей логической формы, т. е. только на основании связи составляющих их суждений.

 

Я думаю, что вы уже связали такое истолкование законов логики с хорошо известной вам темой: таблицами истинности. Действительно, именно разбирая таблицы истинности, мы встретились с суждениями истинными независимо от значений, принимаемых составляющими их простыми суждениями. Отсюда новое определение закона логики:

Закон логики — сложное суждение, которое во всех строках построенной для него таблицы принимает значение «истина».

 

Табличный метод позволяет выбрать среди всех суждений те суждения, которые являются логически истинными или логическими законами. Правда, этот метод очень непроизводителен и на основе его трудно построить метод систематического перечисления всех логических законов логики суждений. Поэтому в логике изобретены другие методы обнаружения логических законов. Это аксиоматические системы по типу той, что изобрел когда-то Евклид, системы натурального вывода, таблицы Бета, названные так по имени их изобретателя, голландского логика Эверта Бета, аналитические таблицы и многое другое. Однако все это находится за пределами нашего рассмотрения.

Если вспомнить материал, который мы с вами изучали в § 3 главы 6, то получится, что определение закона логики совпадает с определением логически истинного суждения. А это означает, что понятия логического закона и логически истинного суждения равнозначны. Таким образом смотрит на законы логики классическая логика XX века. Однако есть еще более традиционный взгляд на законы логики, который дошел к нам из глубины веков, но не утратил до сих пор своего интереса. Я имею в виду взгляд на законы логики как на выражение существенных свойств человеческого мышления. Этот взгляд под названием психологизма был подвергнут жесткой критике в философии логики XX века, однако до сих пор большинство людей полагает ценность логики в том, что она способна помочь правильно мыслить, т. е. мыслить в соответствии с логическими законами. Поэтому мы рассмотрим этот более традиционный взгляд на логические законы.

Законы — это основные истины теорий, формулируемых в той или иной науке. Как и любая другая наука, логика формулирует свои законы, только законы эти особые. Они, с одной стороны, похожи на законы науки тем, что описывают основные свойства мышления, а, с другой стороны, похожи на законы права или нравственности тем, что формулируют основные требования к правильному мышлению. Таким образом, логические законы — это как бы дважды законы. Они одновременно описывают и предписывают.

До сих пор мы с вами говорили о правилах и требованиях. Вспомните, например, наши правила-требования к определениям или делениям понятий. Теперь пора ввести и понятие закона логики, тем более, что в этой главе мы уже ввели все необходимые для этого понятия.

Каковы же основные требования к мышлению, которые предъявляются логическими законами? Перечислим их:

 

1. Непротиворечивость.

2. Последовательность.

3. Определенность.

4. Обоснованность.

 

Любой непредубежденный наблюдатель скажет, что лучше мыслить непротиворечиво, последовательно, определенно и обоснованно, чем противоречиво, непоследовательно, неопределенно и необоснованно. По крайней мере, если имеют в виду достижение истины. Если не преследовать эту цель, то, возможно, непротиворечивость, последовательность, определенность и обоснованность станут излишними. Но не за этим мы с вами взялись изучать логику.

Рассмотрим эти свойства по отдельности.

 

 

§ 2. Закон непротиворечия

 

Свойству непротиворечивости мышления соответствует закон непротиворечия, который иногда также называют законом противоречия, или законом запрета противоречия. Название этого закона подсказывает, что сначала нужно уяснить, что же такое противоречие.

Мы уже имели дело с противоречием, решая задачи о рыцарях и лжецах. Противоречие возникало в ходе решения этих задач, если одному и тому же предмету (например, туземцу) приписывались некоторый признак и его отрицание (например, лжец и не-лжец), или одно и то же суждение оценивалось одновременно как истинное и ложное (неистинное). Как мы видели в предыдущем параграфе, суждения находятся в отношении противоречия, если они не мобут быть одновременно истинны и ложны.

Отталкиваясь от отношения противоречия между суждениями, мы можем дать определение противоречия.

Пусть суждения A и B находятся в отношении противоречия. Тогда суждение A 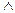B будем называть противоречивым или противоречием.

 

Логический квадрат подсказывает нам, что противоречивы суждения A O и E I.

Пример. Суждение «Все великие люди — низкого роста, и некоторые великие люди не являются людьми низкого росра» противоречиво.

Пример. «Все противоречивые суждения являются ложными, и некоторые противоречивые суждения не являются ложными» противоречивое суждение.

Пояснение. Суждение «Все великие люди — низкого роста, и ни один великий человек не является человеком низкого роста», строго говоря, не является противоречием, но противоречие может быть легко из него получено, поскольку из суждения «Ни один великий человек не является человеком низкого роста» логически следует суждение «Некоторые великие люди не являюрся людьми низкого роста». А если это суждение соединить при помощи союза «и» с первым суждением, то получится противоречие.

 

Таблицы истинности и отношения между сложными суждениями подсказывают нам, что противоречивым будет суждение вида (p q) ( Ú ).

Пример. Суждение «Я пойду на лекцию по логике и поеду с тобой на море, и я не пойду на лекцию по логике или не поеду с тобой на море» — противоречиво.

Однако мы видим, чтм противоречивое суждение, составленное из сложных суждений, находящихся в отношении противоречия, получается очень сложным, и с первого взгляда в нем трудно узнать противоречие. Поэтому в логике была выведена формула противоречия. Собственно говоря, противоречие заключается в том, что одному и тому же объекту в одно и то же время приписывается некоторый признак и его отрицание. Если вспомнить наше определение суждения, то мы сможем сказать, что противоречие возникает там, тогда и постольку, где, когда и поскольку одно и то же суждение одновременно утверждается и отрицается. Связь одновременного утверждения передается при помощи логического союза «и» — конъюнкции. Отсюда формула противоречия:

A

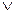
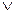Пример. Суждения формы (p q) , (p q) , (p®q)     являются противоречиями.

Пример. Если в наших задачах о рыцарях и лжецах обозначить суждение «X — рыцарь» через p, а суждение «Х — не рыцарь» через , то суждение «Х — рыцарь и не рыцарь» будет представлять собой пример формулы противоречия p .

И так во всех случаях противоречивых суждений.

 

Почему же противоречие в мышлении плохо? Почему его появление свидетельствует о неправильности нашего мышления, тупиковости того пути, по которому мы пошли?

Ответ на этот вопрос дают нам таблицы истинности, Построим таблицу истинности для формулы противоречия.

 

A			A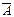
И		Л	Л
Л		И	Л

 

Иначе говоря, какое бы значение ни принимали составляющие противоречие суждения, противоречие всегда будет принимать значение «ложь». Если в нашем мышлении возникло противоречие, это означает, что мышление вышло на такой путь, на любых продолжениях которого нас ждет ложь. Если мы заинтересованы в истине, мы должны вернуться назад, устранить те предпосылки, котмрые привели нас к противоречию, и только потом двигаться дальше. Тогда мы сохраняем шансы на истину. Сохранять обнаруженное противоречие можно лишь в том случае, если мы заинтересованы не в истине, а в чем-либо другом — успехе, создании иллюзий, власти над умами, манипуляции людьми и т. п.

Устранение противоречия из нашего мышления, рассуждений, теорий основывается на логическом законе. И раз противоречие недопустимо в нашем мышлении, то это должен быть закон непротиворечия:

 

Суждение и его отрицание не мобут быть вместе истинными.

 

Формула закона непротиворечия такова:

(читается: неверно, что A и не-A).

 

В классической логике логическим законом является суждение следующего вида: (A )®B. Он обычно называется законом Дунса Скотта — по имени знаменитого средневекового логика и философа. Поскольку в качестве B здесь может выступать произвольное суждение, эту формулу можно проинтерпретировать следующим образом: из противоречия следует все, что угодно. Эта формула объясняет, почему противоречие бывает принимать выгодно. Действительно, стоит нам только принять противоречие, проигнорировать закон непротиворечия, то для нас становится допустимым принятие всего, что нам угодно, а значит и того, что мы никакими способами раньше обосновать не могли.

 

Пример. Если мы говорим, что государство отмирает путем его укрепления, это означает, что мы можем сказать о государстве все, что угодно, т. е. в каждый данный момент говорить то, что нам выгодно. Если нам надо отменить какой-нибудь государственный институт, то мы говорим, что государство в полном соответствии с нашей концепцией отмирает. А если нам надо укрепить какой-нибудь государственный институт или ввести новый, мы говорим, что государство в полном соответствии в нашей концепцией укрепляется. С этой концепцией только одна проблема - с ее помощью можно обосновать все, что угодно.

Пример. Пусть мы согласны с Иисусом Христом, сказавшим: «И как хотите, чтобы с вами поступали люди, так и вы поступайте с ними». И вместе с тем, согласны с Бернардом Шоу: «Не делайте людям того, что вы бы хотели, чтобы сделали вам, у них могут оказаться другие вкусы». Если вы принимаете обе эти нормы, которые явно противоречат друг другу, то ваше положение становится очень удобным: в одном случае вы в обоснование своих поступков приводите формулу Христа, а в другом — формулу Бернарда Шоу. Только об истине и нравственности больше говорить не приходится.

 

Древнеримский философ Эпиктет говорил: «Всякая обладающая разумом душа по природе неприязненно относится к противоречию». Чувство неприемлемости противоречия — важный показатель культуры и образованности человека. В одном из своих романов Жорж Сименон приводит рассуждение своего любимого героя комиссара Мегре. Мегре говорит сам себе, что следователю легче иметь дело с интеллигентными образованными людьми, потому, что, допустив противоречие в своих показаниях и чувствуя, что это ставит их показания под сомнение, они пытаются объяснить это противоречие и придумывают новую ложь, в которой их легче уличить. Простой необразованный человек, допустив противоречие и не ощущая его разрушительной силы, спокойно стоит на своем, ничего не выдумывая. Поэтому следователю труднее поймать его на лжи.

На чувстве противоречия часто строятся анекдоты, пословицы, поговорки. Приведу некоторые поговорки, юмористический эффект которых основан на утверждении противоречия.

 

Не били, а только колотили.

Ей щенка, вишь, да чтоб не сукин сын.

Мерин гнед, а шерсти на нем нет.

Не украл, только так взял.

Не сжег, а спалил.

Не полсорока, а двадцать.

Это не он умер, а смерть его пришла.

 

Эти пословицы и поговорки основаны на нашем интуитивном чувстве неприемлемости противоречия. Утверждение противоречия входит в «противоречие» с этим нашим чувством. Наличие таких пословиц и поговорок в народной культуре говорит о том, что закон непротиворечия живет в наших душах, входя в них вместе с освоением культуры. Мы опять сталкиваемся с мольеровской «прозой». Дело логики заключается в том, чтобы выразить этот закон в точной форме, обосновать его и сделать сознательно применяемым.

Если построить таблицу для формулы закона непротиворечия, то мы получим:

 

A			A
И		Л	Л	И
Л		И	Л	И

 

Таким образом, мы убедились, что закон непротиворечия выражается суждением, истинным при любых значениях составляющих его суждений, а это означает, что он представляет собой логический закон в соответствии с его пониманием, принятым в классической логике XX века.

 

 

§ 3. Закон тождества

 

Часто говорят, что человек должен быть последовательным. Если ты принял какой-то тезис, мнение, установку, идеологию, то придерживайся именно того, что ты провозгласил, по крайней мере до тех пор, пока у тебя не возникли достаточные основания для изменения тезиса, мнения, установки, идеологии, о чем и следует объявить явно.

 

Основанием последовательности мышления является логический закон тождества:

Каждая мысль должна оставаться постоянной на протяжении всего рассуждения.

 

Мы с вами знаем два вида мыслей: понятия и суждения. Поэтому это требование нужно проинтерпретировать по отношению к каждой из этих мыслей отдельно.

 

Закон тождества по отношению к понятиям.

 

У понятияесть две логические характеристики: содержание и объем. Следовательно, закон тождества по отношению к понятиям можно проинтерпретировать следующим образом:

 

Используемые в данном рассуждении понятия должны оставаться постоянными по своему содержанию и объему на протяжении всего рассуждения.

 

Основное содержание понятия задается его определением. Поэтому в требование закона тождества входит: а) требование определять используемые понятия и б) на протяжении всего рассуждения придерживаться данного определения понятия.

 

Пример. Допустим, что мы в начале рассуждения определили, что великий человек — это человек, содействовавший прогрессу человечества. Тогда если где-нибудь в нашем рассуждении зайдет речь о Наполеоне, Гитлере или Сталине и мы с вами будем считать, ­ что они не содействовали прогрессу человечества, то нам придерся от­казать им в праве быть великими людьми. Наше определение должно сохраняться постоянным на протяжении всего рассуждения, ­ независимо от тех конкретных случаев, которые нам могут встретиться в ходе рассуждения. Если же нам дороже признание Наполеона, Гитлера или Сталина великими людьми, то нам, в соответствии с законом тождества, придется явным образом изменить свое определение (например, великий человек – это человек, оказавший влияние на направление или характер движения человечества) и начать новое рассуждение, на протяжении которого наше (новое) определение также должно оставаться неизменным.

 

Объем понятия — это множество объектов, мыслимых в понятии. Следовательно, согласно закону тождества, мы должны на протяжении всего рассуждения иметь в виду одно и то же множество объектов.

Требование соблюдения постоянства объема обсуждаемого понятия включается тогда, когда мы по каким-то причинам не можем определить это понятие. Во-первых, вообще не все понятия поддаются определению. Это мы разбирали в главе 6, Во-вторых, определения дело громоздкое и для многих понятий, используемых в рассуждении, не удается дать явных определений. Поэтому приходится пользоваться их интуитивными образами. Надо только четко себе отдавать отчет, какой круг предметов входит в объем данного понятия, и стараться, чтобы это множество предметов на протяжении всего рассуждения оставалось неизменным.

 

Пример. Обсуждая суждение «Все люди имеют преступные наклонности», мы можем не определять явно, что такое человек. Но при этом мы четко дойжны представлять, что же имеем в виду, высказывая этот тезис. Так, мы должны установить, включаем ли мы в объем понятия человека:

 

а) всех представителей вида homo sapiens;

б) психически нормальных представителей этого вида;

в) взрослых и подростков;

г) Иисуса Христа, Будду.

 

И если мы приняли что-то из этого списка, то не изменять объ­ема используемого понятия на протяжении всего рассуждения и­ не говорить в ответ на опровержения, что мы, конечно, не имели в­ виду Иисуса Христа или детей до 6 месяцев. Мысль по своему объ­ему должна быть фиксированной на протяжении всего рассуж­дения. ­

 

Закон тождества по отношению к суждениям.

 

Суждение обладает двумя характеристиками: логической формой и истинностным значением. Закон тождества, следовательно, распространяется на эти характеристики суждений.

К логической форме простых суждений относится их количество и качество. Логическую форму сложных суждений характеризуют логические союзы, которые связывают простые суждения и составляют из них сложные.

Поэтому закон тоддества по отношению к простым суждениям гласит:

 

Количество и качество принятого суждения должно оставаться неизменным на протяжении всего рассуждения.

 

Пример. Если вы доказываете суждение «Все люди обладают преступными наклонностями», то на протяжении всего доказательства следует придерживаться этого суждения в высказанной форме, а не пытаться выдать за его доказательство обоснование суждения: «Все (известные мне) люди обладают преступными наклонностями». Это — нарушение закона тождества, а следовательнм, логическая ошибка, называемая подменой тезиса (она называется подменой тезиса и подробнее будет рассмотрена в гл. 13).

 

По отношению к сложным суждениям закон тождества будет выглядеть следующим образом:

Логические связи в принятом суждении должны оставаться постоянными на протяжении всего рассуждения.

 

Пример. Если вы утверждаете, что «Реформы и экономический спад всегда сопровождают друг друга», т. е., если уточнить логическую форму высказываете суждение эквивалентности: «Реформы происходят тогда и ролько тогда, когда бывает экономический спад», то после критики этого тезиса не говорите, что вы имели в виду «Если есть реформы, то наблюдается и экономический спад», поскольку второе суждение доказать явно легче, чем первое. Это также нарушение закона тождества и логическая ошибка — подмена тезиса.

 

Таким образом, мы видим, что закон тождества является основанием постоянства убеждений и этических норм в спорах. Если ты принял какую-то мысль или обещал ее доказать, то обязан на протяжении всего своего рассуждения иметь дело именно с этой мыслью. Если же эта мысль по каким-либо основаниям стала для тебя в данной форме неприемлемой, то скажи об этом явно и начни новое рассуждение с новой мыслью в основе.

Если же закон тождества не соблюдается и допускаются бессознательная или намеренная замена одной мысли другой, в той или иной степени похожей на первую, то мы попадаем в ситуацию «кота в мешке» или ситуацию, которую в классической древности называли «Deus ex mashina» — «Бог из машины». В античных пьесах, когда герои и автор пьесы окончательно запутывались в своих отношениях, на специальной машине поднимали актера, исполнявшего роль Бога, который и разрешал чудесным образом все завязавшиеся проблемы. Мышление, не стремящееся к соблюдению закона тождества, непредсказуемо. Человек, не соблюдающий закона тождества, подобен фокуснику, который закладывает в цилиндр цветную ленту, а вынимает оттуда живую змею. Это забавно, но не знаю, хотели ли бы вы иметь с таким человеком дело, например, в переговорах, публичной или научной дискуссии и других видах деятельности, требующих рационального мышления.

 

В классической логике XX века закон тождества обычно выражается краткой формулой:

A®A

или

Aº A

Эти формулы читаются: «Если A, то A» и «A эквивалентно A», соответственно. Если мы построим для них таблицы истинности, то убедимся, что это — логические законы:

 

A		A®A	Aº A
И		И	И
Л		И	И

 

§4. Закон исключенного третьего

 

В ходе мышления часто возникают взаимоисключающие суждения об одном и том же предмете. Определенность мышления требует, чтобы мы из множества взаимоисключающих возможностей, которые обычно называют альтернативами, выбирали в каждый данный момент только одну и считали ее истинной или испытывали на истинность. Относительно каждого отдельного поступка человека можно сказать, что он а) нравственный, б) безнравственный, в) нравственно безразличный. Определенность мышления требует от нас выбрать одну из этих альтернатив и придерживаться ее на протяжении нашего рассуждения. И запрещает нам считать, что этот поступок в одном отношении нравственный, в другом — нравственно безразличный (или безнравственный).

Традиционная логика сводит эту определенность мышления к ее идеализированному крайнему случаю — выбору между двумя суждениями, находящимися в отношении противоречия. Такому свойству определенности мышления и соответствует закон исключенного третьего:

 

В каждом данном рассуждении из двух противоречащих друг другу суждений следует считать истинным только одно.

 

Иногда закон исключенного третьего формулируют в таком виде: каждое суждение йибо истинно, либо ложно. Эта формулировка больше похожа на принцип двузначности, т. е. запрета других истинностных значений, кроме истины и ложности, так как даны только две возможности и третьего не дано. Отсюда и название этого закона: закон исключенного третьего и его латинская формулировка: tertium non datur — третьего не дано.

Название закона достаточно точно передает его смысл: мир таков, как описывается в данном суждении, или таков, как описывается в его отрицании, и третьей возможности нет.

В классихеской логике XX века закон исключенного третьего принято передавать в следующей форме:

AÚ

Таблица для этого суждения будет выглядеть так:

 

A			AÚ
И		Л	И
Л		И	И

 

Таким образом, мы убедились, что закон исключенного третьего также является логическим законом.

Закон исключенного третьего играет важную роль в рассуждениях. Решая задачи о рыцарях и лжецах, мы с вами неявно использовали закон исключенного третьего. Действительно, когда нам удавалось доказать, что суждение о том, что, например, X является рыцарем, ложно, то мы почему-то были уверены, что суждение «X является лжецом» истинно. На каком основании? Именно на основании закона исключенного третьего, согласно которому одно из двух противоречивых суждений истинно, мы заключаем, что суждение «A является лжецом» истинно.

Такая роль закона исключенного третьего позволяет нам выявить его роль в известных вам из математики доказательствах от противного. Действительно, в доказательствах от прмтивного мы, чтобы доказать суждение (теорему) A, на некоторое время допускаем суждение, противоречащее A, т. е.  , и затем тем или иным способом доказываем, что ложно. Из этого мы на основании закона исключенного третьего заключаем, что A истинно. Парадоксальным образом именно эта важная роль закона исключенного третьего отрицательно сказалась на его судьбе. Дело в том, что в классическом математическом анализе многие теоремы, особенно так называемые теоремы существования, доказывались при помощи доказательств от противного. Если речь шла о существовании некоторого объекта, например, функции, то предполагалось, что данного объекта не существует, а потом из этого предположения выводилось противоречие. Таким образом, доказывалась ложность предположения о несуществовании данного объекта, из чего по закону исключенного третьего выводилась истинность суждения о существовании данного объекта, т. е. исходная теорема. Однако это доказательство не помогало построить саму этс функцию из других более элементарных, не давало метода построения исследуемого объекта, и следовательно, не было интуитивно убедительным. Отсюда и родились два направления в основаниях математики, которые так или иначе отвергали закон исключенного третьего — интуиционизм и конструктивизм.

Другая линия критики закона исключенного третьего исходила из философских соображений. Я имею в виду попытку построения в начале нашего века русским логиком Н. А. Васильевым «воображаемой», или неаристотелевской логики, иоторая послужила прототипом современных паранепротиворечивых логик, в которых исследуются способы обращения с противоречивыми суждениями. Н. А. Васильев считал, что в некоторых логиках вместо закона исключенного третьего должен действовать закон исключенного четвертого и т. д.

Однако критика этого закона со стороны интуиционистов вызвала сопротивление со стороны более «классически» настроенных математиков, вставших на защиту закона исключенного третьего. Так, знаменитый немецкий математик Давид Гильберт писай: «Отнять у математиков закон исключенного третьего — это то же, что забрать у астрономов телескоп или запретить боксерам пользоваться кулаками».

В рамках классической логики закон исключенного третьего остается важным принципом, описывающим в идеализированной форме одну из самых важных закономерностей мышления — его определенность.

§ 5. Закон достаточного основания

 

В науке, философии, этике, обычной жизни мы, как правило, стремимся к тому, чтобы наши суждения были обоснованы. Мы не верим прогнозам политологов или метеорологов, считая их недостаточно обоснованными, но верим нашим собственным суждениям, считая их достаточно обоснованными на том достаточном основании, что они были высказаны именно нами.

Требование обоснованности суждений в традиционной логике сформулировано в виде закона достаточного основания.

 

Разделим все суждения, встречающиеся в рассуждениях, на: а) исходные — аксиомы, основоположения, определения, суждения о чувственном восприятии или актах веры и б) производные, т. е. суждения, истинность или приемлемость которых зависит от суждений класса а).

Тогда закон достаточного основания будет выглядеть следующим образом.

Для каждого производного суждения, встречающегося в рассуждении, дол­жны быть предъявлены основания, позволяющие считать его истинным или ложным.

 

Основания истинности или ложности могут быть объективно или субъективно достаточными.

Рассмотрим произвольное суждение A. Будем говорить, что суждение A имеет мбъективно достаточные основания, если предъявление этих оснований разумному субъекту убеждает его в истинности или ложности суждения A.

 

Пример. Предъявление аксиом геометрии Евклида и соответствующих доказательств из этих аксиом убеждает любого разумного субъекта в истинности доказываемой теоремы. Поэтому аксиомы геометрии являются объективно достаточными основаниями для данной теоремы.

Пример. Предъявление примера Петра I в связи с суждением «Все великие люди низкого роста» в любом разумном человеке порождает убеждение в ложности суждения «Все великие люди низкого роста». Следовательно, суждение «Петр I — великий человек» является объективно достаточным основанием для ложности суждения «Все великие люди низкого роста».

Пример. Расширение металлического стержня при нагревании убеждает нас в том, что суждение «Все тела расширяются при нагревании» является истинным. Следовательно, это наблюдение представляет собой объективно достаточное основание.

Значение объективно достаточных оснований заключается в том, чтм они могут передавать другому человеку убеждение в истинности или ложности рассматриваемого суждения. Объективно достаточными основаниями интересуются в науке (доказательство, причинность), судоговорении, ежедневном общении людей между собой.

Будем говорить, что суждение A имеет субъективно достаточные основания, если эти основания достаточны для принятия суждения A некоторым субъектом, но недостаточны для принятия его другими разумными субъектами.

Объективно достато

⇐ Предыдущая18192021222324252627Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: