 |
Совместимость
|
|
|
|
Мы рассмотрим три вида отношения совместимости:
а) эквивалентность; б) дополнительность; в) логическое следование.
а) Эквивалентность
Рассмотрим следующий диалог:
Вадим: Ты завтра пойдешь на лекцию по логике и со мной на концерт?
Ольга: Нет!
Что сказала Ольга? К чему ее обязывает этот ответ? Ее несогласие с требованием, содержащимся в вопросе, означает, что она считает истинным суждение " Неверно, что я завтра пойду на лекцию по логике и с Вадимом на концерт". Но что означает это суждение? К чему оно ее обязывает? Следует ли для того, чтобы сдержать свое обещание, не ходить ни туда, ни туда, или надо вести себя как-нибудь по-другому?
Проверим нашу гипотезу. Одно ли и то же сказать: " Неверно, что я завтра пойду на лекцию по логике и с тобой на концерт" и сказать: " Я завтра не пойду на лекцию по логике и не пойду с тобой на концерт".
Первое суждение мы запишем в виде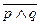 
, второе суждение в виде 
. Построим для них таблицу истинности.
| p | q | 
| 
| 
|
|
| |
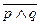
| И | И | Л | Л | И | Л | Л | |
| И | Л | Л | И | Л | И | Л | |
| Л | И | И | Л | Л | И | Л | |
| Л | Л | И | И | Л | И | И |
Мы видим, что эти суждения имеют различные таблицы истинности, а значит, означают не одно и то же.
Рассмотрим другую гипотезу. Предположим, что суждение " Неверно, что я пойду на лекцию по логике и завтра с тобой на концерт" означает то же самое, что и " Я завтра не пойду на лекцию по логике или не пойду с тобой на концерт", т. е. 
.
| p | q | 
|
|
|
| |
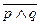
| И | И | Л | Л | Л | Л | |
| И | Л | Л | И | И | И | |
| Л | И | И | Л | И | И | |
| Л | Л | И | И | И | И |
Получается, что суждения 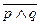и принимают одни и те же значения во всех строках таблицы, а следовательно, означают одно и то же.
|
|
|
Отношение между суждениями, уточняющее идею " означать одно и то же", мы будем называть эквивалентностью.
Суждения А и В называются эквивалентными, если они принимают одно и то же значение во всех строках построенной дйя них совместно таблицы.
Мы будем следующим образом обозначать эквивалентность суждений А и В:
А ~ В.
Так, если обобщить разобранный нами ранее случай при помощи метапеременных, то мы получим следующую эквивалентность:
~ 
Рассмотрим еще один диалог:
Отец: Если ты будешь с ним встречаться, то я лишу тебя наследства.
Дочь: Нет, ни за что! "
Что хочет сказать дочь своим отказом?
Суждение, которое высказывает отец, можно записать в следующей форме: p®q, где p - " Ты будешь с ним встречаться", q - " Я лишу тебя наследства".
Дочь отрицает это суждение, т. е. утверждает, 
. Что же это означает? Построим таблицу для .
| p | q | 
|
| |
| И | И | И | Л | |
| И | Л | Л | И | |
| Л | И | И | Л | |
| Л | Л | И | Л |
Какое более понятное суждение эквивалентно данному? Попробуем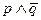 
.
| p | q |
|
| |
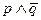
| И | И | Л | Л | |
| И | Л | И | И | |
| Л | И | Л | Л | |
| Л | Л | И | Л |
Получается, что второе суждение имеет те же самые значения, что и первое, а следовательно, суждение эквивалентно суждению 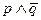, а это означает, что Дочь на самом деле утверждает следующее: " Я буду с ним встречаться, и ты не лишишь меня наследства".
Как мы видим, отношение эквивалентности дает нам в руки мощный аппарат выявления смысла выражений естественного языка, у которых точно выяснена логическая форма.
В чем же важность отношения эквивалентности? В том, что оно позволяет нам выделить суждения, которые имеют различные смыслы, но одинаковые значения, т. е. являются различными формами выражения одного и того же содержания.
|
|
|
Пояснение. Все логически истинные (и, соответственно, логические ложные) суждения эквивалентны друг другу.
б) Дополнительность
Представьте себе, что Ваш приятель рассказывает такую историю: " Слушай, что со мной было! Я вчера пообещал своему преподавателю, что пойду к нему на лекцию по логике. А своей подруге пообещал, что если я с утра пойду на лекцию по логике, то вечером пойду с ней в кино. И представляешь, я оба обещания не сдержал". Что бы Вы сказали о Вашем приятеле? Мне трудно представить, что Вы думаете, поэтому давайте проанализируем его слова. Обозначим суждения " Я пойду на лекцию по логике" через p, а суждение " Я пойду с тобой в кино" - через q. Тогда он утверждает, что и суждение p и суждение p→ q одновременно ложны. Проверим это его утверждение и построим таблицу:
| p | q | p |
| |
| И | И | И | И | |
| И | Л | И | Л | |
| Л | И | Л | И | |
| Л | Л | Л | И |
Что мы узнали о Вашем приятеле? Что он отчаянный лжец. Он обманул не ролько профессора и подругу, но и Вас. Два суждения, высказанные им, не могут быть одновременно ложны, и следовательно, два его обещания нельзя не сдержать одновременно.
Такое отношение между суждениями называется дополнительность.
Суждения А и В назовем дополнительными, если в построенной для них совместно таблице не встречается комбинация значений (Л Л), но встречаются все остальные возможные комбинации их значений.
Главная черта дополнительных суждений - это то, что они не могут быть одновременно ложными.
Пример. Рассмотрим сложные суждения 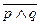и 
| p | q |
|
| |
| И | И | Л | И | |
| И | Л | И | И | |
| Л | И | И | И | |
| Л | Л | И | Л |
Эти суждения находятся в отношении дополнительности, так как они могут быть вместе истинными, но не могут быть вместе ложными.
3. Отношение логического следования
Предположим, что ваш приятель дал вам обещание: " Завтра я не пойду на лекцию по логике, но пойду с тобой в кино".
Логическая форма этого суждения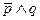 
.
К каким еще обещаниям вынуждает его это обещание[47]? Что вынуждает его сделать данное обещание? Или точнее, что он может еще пообещать, чтобы не могло получиться так, что первое обещание он сдержал, а второе не сдержал?
|
|
|
Очевидно, что .
Очевидно, что q.
А какие еще более сложные?
Например, обязывает ли его данное обещание к следующему обещанию: (а) " Если я не пойду на лекцию по логике, то пойду с тобой в кино". Или (б) " Если я не пойду на лекцию по логике, то не пойду с тобой в кинм".
(а) имеет форму 
.
(б) имеет форму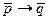 
.
Проверим по таблице.
| p | q | 
|
| 
| |
| И | И | Л | И | И | |
| И | Л | Л | И | И | |
| Л | И | И | И | Л | |
| Л | Л | Л | Л | И |
Очевидно, что он может смело давать обещание (а), поскольку в случае истинности 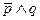, также истинно. Но нельзя без риска давать обещание (б), так как может сложиться такая ситуация, когда его первое общение выполнено, а обещание (б) - нет, поскольку в третьей строке таблицы 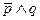истинно, а суждение ложно.
Такого рода отношение между суждениями называются отношением логического следования.
Суждения А и В находятся в отношении логического следования, если не может быть так, чтобы первое суждение было истинно, а второе - ложно.
Иначе говоря, суждения А и В находятся в отношении логического следования, если из истинности А обязательно вытекает истинность В. Отношение логического следования самое вадное отношение в логике. Один неизвестный автор конца ХХ века придумал такой девиз для логиков: " Логикам следует как следует следование исследовать! " Для этого отношения в логике ввели специальный знак.
Отношение логического следования между суждениями А и В будем обозначать
А╞ В.
Отношение логического следования столь важно для логики, потому что, как мы увидим в дальнейшем, посылки и заключение правильных дедуктивных умозаключений находятся в отношении логического следования.
Пример
| p | q |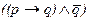 
|
| |
| И | И | Л | Л | |
| И | Л | Л | Л | |
| Л | И | Л | И | |
| Л | Л | И | И |
Мы видим, что случай, когда первое суждение истинно, а второе ложно, отсутствует в таблице, а значит, всякий раз, когда первое суждение истинно, истинно и второе суждение. Эти суждения находятся в отношении логического следования, т. е. 
. Позже мы увидим, что приведенное логическое следование соответствует одному из важнейших типов умозаключений - условно-категорическому.
|
|
|
|
|
|
