 |
Измерение информации в теории информации (информация как снятая неопределенность)
|
|
|
|
В теории информации количеством информации называют числовую характеристику сигнала, не зависящую от его формы и содержания и характеризующую неопределенность, которая исчезает после получения сообщения в виде данного сигнала - в этом случае количество информации зависит от вероятности получения сообщения о том или ином событии.
Для абсолютно достоверного события (событие обязательно произойдет, поэтому его вероятность равна 1) количество вероятности в сообщении о нем равно 0. Чем вероятнее событие, тем больше информации о нем несет сообщение.
Лишь при равновероятных ответах ответ "да" или "нет" несет 1 бит информации. Оценка количества информации основывается на законах теории информации. Сообщение имеет ценность, несет информацию, когда мы узнаем и понимаем смысл данного сообщения.
Какое количество информации содержится, к примеру, в тексте романа "Война и мир", в фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро.
А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является вывод: в определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных.
Теория информации как самостоятельная научная дисциплина была основана Клодом Шенноном в конце 40-х годов 20 века. Предложенная им теория основывалась на фундаментальном понятии количественной меры неопределенности – энтропии и связанного с нею понятия количества информации.
Сигнал – это материальный носитель информации (предмет, явление, процесс) в пространстве и во времени. Любой сигнал неразрывно связан с определенной системой, которая является системой связи или системой передачи информации и состоит из следующих модулей: источник, передатчик, канал связи, приемник и адресат. Источник информации задает некоторое множество сообщений. Генерация определенного сообщения заключается в выборе его из множества всех возможных. Сообщения бывают дискретными и непрерывными. Светофор или передача сообщения с помощью азбуки Морзе – примеры дискретного сигнала.
|
|
|
Особым видом сигналов являются знаки, которые в отличие от сигналов естественного происхождения создаются самоорганизующимися системами и предназначаются для передачи и хранения информации. Есть знаки, входящие в четко организованную систему, и внесистемные знаки. Например: знаки дорожного движения, система цветов светофора, музыка, речь и языки, как естественные, так и искусственные. Внесистемные знаки – это или остатки некогда существовавших знаковых систем, или знаки, созданные временно, обычно в небольших коллективах людей. Например, языки жестов и поз.
В теории информации и кодировании принят энтропийный подход к измерению информации, который основан на том, что факт получения информации всегда связан с уменьшением разнообразия или неопределенности (энтропии) системы. Неопределенность может быть интерпретирована в смысле того, насколько мало известно наблюдателю о данной системе, энтропия системы снизилась, так как для наблюдателя система стала более упорядоченной.
При энтропийном подходе под информацией понимается количественная величина исчезнувшей в ходе какого-либо процесса (испытания, измерения и т.д.) неопределенности. При этом в качестве меры неопределенности вводится энтропия [1].
Энтропия – мера внутренней неупорядоченности информационной системы.
|
|
|
Энтропия увеличивается при хаотическом распределении информационных ресурсов и уменьшается при их упорядочении.
На основе понятий энтропии и количества информации в теории информации введены важные характеристики сигналов и информационных систем:
скорость создания информации;
скорость передачи информации;
избыточность;
пропускная способность каналов связи.
Одним из самых замечательных результатов теории информации является доказательство, что при любых помехах и шумах можно обеспечить передачу информации без потерь.
Первая теорема Шеннона гласит, что при скорости создания информации меньшей пропускной способности канала можно передавать информацию со сколь угодно малой вероятностью ошибок, несмотря на шумы.
Шеннон сформулировал энтропию как меру хаоса в противовес количеству информации как меры упорядоченности структур.
Рассмотрим некоторую сложную систему и проследим ее эволюцию. Пусть эта система представляет собой находящийся в сосуде газ, состоящий из огромного числа беспорядочно движущихся молекул. Мы не знаем точного положения и скорости в каждый момент времени каждой частицы газа, но нам известны макропараметры: давление, объем, температура и состав газа. Фактически мы должны рассчитать число способов, которыми можно осуществить внутренние перестройки в системе, чтобы наблюдатель не заметил изменений макросостояния системы. При этом предполагается неотличимость атомов друг от друга.
Если в системе, состоящей из одного атома, произошло его энергетическое возбуждение, нам это может стать известно по значению температуры. При этом возможно только одно распределение возбуждения в системе равному единице. Энтропия связана с распределением следующим образом:  . В нашем случае
. В нашем случае  , а значит, система обладает нулевой энтропией.
, а значит, система обладает нулевой энтропией.
В системе из ста атомов, распределение возбуждения может быть осуществлено ста способами, т.е.  ,
,  . Энтропия системы выросла и стала хаотичной, поскольку мы не знаем, где находится в каждый момент возбужденный атом.
. Энтропия системы выросла и стала хаотичной, поскольку мы не знаем, где находится в каждый момент возбужденный атом.
Принято считать, что любая система стремится к состоянию равновесия, т.е. растет энтропия системы. Однако второе начало термодинамики (закон сохранения энтропии и информации) требует компенсировать рост энтропии. Информация и является средством компенсации.
|
|
|
В настоящее время получили распространение подходы к определению понятия "количество информации", основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте.
Р. Хартли предложил в качестве меры неопределенности логарифм от числа возможностей, т.е. процесс получения информации рассматривает как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определяет как двоичный логарифм N:  - формула Хартли.
- формула Хартли.
Обычно количество информации представляется в виде: 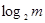 , где m - число возможных выборов. Тогда стандартной единицей количества информации будет выбор из двух возможностей. Такая единица получила наименование бит и представляется одним символом двоичного алфавита: 0 или 1.
, где m - число возможных выборов. Тогда стандартной единицей количества информации будет выбор из двух возможностей. Такая единица получила наименование бит и представляется одним символом двоичного алфавита: 0 или 1.
Пример: нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется:  .Т. е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.
.Т. е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.
Другие примеры равновероятных сообщений: при бросании монеты: "выпала решка", "выпал орел"; на странице книги: "количество букв чётное", "количество букв нечётное".
В некоторых случаях, когда однозначно нельзя ответить на вопросы распределения вероятности, для определения количества информации уже нельзя использовать формулу Хартли.
Пример: являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
|
|
|
Формула Шеннона:
 ,
,
где рi - вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Если вероятности  равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
Кодирование информации
Кодирование информации - это процесс формирования определенного представления информации [3].
В более узком смысле под термином кодирование часто понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки.
Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация (звуки, изображения, показания приборов и т.д.) для обработки на компьютере должна быть преобразована в числовую форму. Чтобы перевести в числовую форму музыкальный звук, можно через небольшие промежутки времени измерять интенсивность звука на определенных частотах, представляя результаты каждого измерения в числовой форме. Аналогичным образом можно обрабатывать текстовую информацию. При вводе в компьютер каждая буква кодируется определенным числом, при выводе на внешние устройства для восприятия человеком по этим числам строятся изображения букв. Соответствие между набором букв и числами называется кодировкой символов.
Одну и ту же информацию можно выразить разными способами. Например, каким образом вы можете сообщить об опасности?
Если на вас напали, вы просто можете крикнуть: «Караул!!!»
Если прибор находится под высоким напряжением, то требуется оставить предупреждающий знак;
На оживленном перекрестке регулировщик помогает избежать аварии с помощью жестов.
В театре пантомимы вся информация передается только с помощью мимики и жестов.
Если ваш корабль тонет, то вы передаете сигнал «SOS».
На флоте используют семафорную и флажковую сигнализацию.
В каждом из этих примеров мы должны знать правила, по которым можно отобразить информацию об опасности тем или иным способом.
Правила, по которым можно отобразить информацию тем или иным способом, называются кодом.
Обычно каждый образ при кодировании представлен отдельным знаком.
Знак – это элемент конечного множества, отличных друг от друга элементов. Знак вместе его смыслом называется символом. Набор знаков, в котором определен их порядок, называется алфавитом. Мощность алфавита - количество используемых в нем символов.
Существует множество алфавитов: алфавит кириллических букв (А, Б, В, Г, Д, …); алфавит латинских букв (A, B, C, D, …); алфавит десятичных цифр (1, 2, 3, 4,…,9, 0); алфавит знаков зодиака и др.
|
|
|
Имеются, однако, наборы знаков, для которых нет какого-то общепринятого порядка: набор знаков азбуки Брайля (для слепых); набор китайских иероглифов; набор знаков планет; набор знаков генетического кода.
Особенно важное значение имеют наборы, состоящие всего из двух знаков: пара знаков (+, -); пара знаков «точка», «тире»; пара цифр (0, 1); пара ответов (да, нет).
Наборы знаков, состоящие из 2 символов, называют двоичными - двоичный алфавит (0, 1), двоичный знак получил название БИТ. С появлением электрического телеграфа возникли важнейшие технические коды: азбука МОРЗЕ; набор знаков второго международного телеграфного кода (телекс).
Код используется для представления информации в виде, удобном для хранения и передачи.
Например, для того чтобы закодировать ряд чисел от 0 до 100, во-первых, нужно выбрать какой-то алфавит. Если для каждого числа придумать символ, который будет его обозначать, то потребуется 101 символ. А если чисел будет больше, то данный подход нерационален. Если каждое число представить (закодировать) не одним, а несколькими знаками из нашего алфавита, то в нашем правиле появится понятие длина кода.
Длиной кода – это такое количество знаков, которое используется при кодировании для представления символа. Количество символов в алфавите и длина кода – совершенно разные вещи. Например, в русском алфавите 33 буквы, а слова могут быть длиной в 1, 2, 3 и т.д. буквы.
Коды бывают постоянной и переменной длины. Коды переменной длины применяются в технике довольно редко. Исключением лишь является код МОРЗЕ. Азбука МОРЗЕ – это троичный код с набором знаков: точка, тире, пауза. Паузу необходимо использовать в качестве разделителя между буквами и словами, так как длина кода непостоянна. Если бы длина кода была постоянной, то расположение символов можно было устанавливать при помощи отсчета. В этом случае пауза не нужна. Сообщение будет раскодировано однозначно.
Применение кодов с постоянной длиной позволяет использовать для кодирования всего лишь два знака (двоичный код). Чем меньше букв в алфавите, тем должно быть проще устройство для раскодирования (расшифровки) информационного сообщения. Чем меньше букв в алфавите, тем больше должна быть длина кода.
В процессе развития человеческого общества люди выработали большое число языков кодирования: разговорные языки (русский, английский, хинди и др.); язык мимики и жестов; язык рисунков и чертежей; язык науки (математические, химические и другие символы); язык искусства (музыки, живописи, скульптуры и др.); специальные языки (эсперанто, морской семафор, азбука Морзе, азбука Брайля для слепых и др.); языки программирования (Бейсик, Паскаль, Фортран, Си и др.).
Программирование – это кодирование информации на языке, «понятном» компьютеру.
В компьютерах используется двоичная форма представления данных. Троичное кодирование, несмотря на ряд технических попыток, успеха не имело. Четверичное кодирование в криптографических целях (криптография – тайнопись) использовалось еще в XV веке. Передача сообщения всегда осуществляется во времени. Кодирование требует определенного количества времени, которым зачастую нельзя пренебрегать. При кодировании могут ставиться определенные цели и применяться различные методы.
Наиболее распространенные цели кодирования:
экономность (уменьшение избыточности сообщения, повышение скорости передачи или обработки информации);
надежность (защита от случайных искажений);
сохранность (защита от нежелательного доступа к информации);
удобство физической реализации (двойное кодирование информации в компьютере);
удобство восприятия (схемы, таблицы).
|
|
|


