Двоичная система счисления

В современной вычислительной технике, в устройствах автоматики, связи используется двоичная система счисления - система счисления с наименьшим возможным основанием, где для изображения числа используются две цифры: 0 и 1.

Двоичная система счисления имеет ряд преимуществ перед другими системами:

для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток - нет тока, намагничен - не намагничен и т.п.);

представление информации посредством только двух состояний надежно и помехоустойчиво;

возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

двоичная арифметика намного проще десятичной.

Недостаток двоичной системы - быстрый рост числа разрядов, необходимых для записи чисел, т.е. в громоздкости записи чисел, но это не имеет существенного значения для ЭВМ. Если возникает необходимость кодировать информацию «вручную», например, при составлении программы на машинном языке, предпочтительнее оказывается пользоваться восьмеричной, или шестнадцатеричной системой счисления.

Произвольное число X в двоичной системе представляется в виде полинома:

,

где каждый коэффициент аi может быть либо 0, либо 1.

Пример: Двоичное число - 1011012

,

т.е. .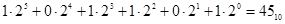

Для отделения целой части от дробной используется точка (запятая). Значение веса разрядов справа от точки (запятой) равно основанию двоичной системы (2), возведенному в отрицательную степень. Такие веса - это дроби вида: 1/2, 1/22, 1/23, 1/24, 1/25 или 1/2, 1/4, 1/8, 1/16.

Каждая позиция, занятая двоичной цифрой, называется бит. Бит является наименьшей единицей информации в ЭВМ. Наименьшим значащим битом (МЗР) называют самый младший двоичный разряд, а самым старшим двоичным разрядом - наибольший значащий бит (СЗР). В двоичном числе эти биты имеют, соответственно, наименьший и наибольший вес. Обычно двоичное число записывают так, что старший значащий бит является крайним слева.

Восьмеричная система счисления

В восьмеричной системе счисления базисными числами являются 0, 1, 2, 3, 4, 5, 6, 7. Запись любого числа в этой системе основывается на его разложении по степеням числа восемь с коэффициентами, являющимися указанными выше базисными числами.

Произвольное число X в восьмеричной системе представляется в виде полинома:

,

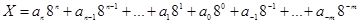где каждый коэффициент аi может быть 0, 1, 2, 3, 4, 5, 6, 7.

Например, десятичное число 83,5 в восьмеричной системе будет изображаться в виде 123,48 и в виде полинома:

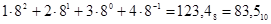
Восьмеричная система счисления не нужна ЭВМ в отличие от двоичной системы. Она удобна как компактная форма записи чисел и используется программистами (например, в текстах программ для более краткой и удобной записи двоичных кодов команд, адресов и операндов).

В восьмеричной системе счисления вес каждого разряда кратен восьми (1/8), поэтому восьмиразрядное двоичное число позволяет выразить десятичные величины в пределах 0-255, а восьмеричное охватывает диапазон 0 - 99999999.Т. к.8=23, то каждый восьмеричный символ можно представить трехбитовым двоичным числом.

Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число влево (для целой части) и вправо (для дробной) от точки (запятой) на группы по три разряда (триады) и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются необходимым количеством незначащих нулей.

Перевод из восьмеричной системы счисления в двоичную систему осуществляется путем представления каждой цифры восьмеричного числа трехразрядным двоичным числом.