Что такое система счисления

Системой счисления называется совокупность приемов наименования и записи чисел [7].

Система счисления - это способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.

В любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно.

В современном мире наиболее распространенным является представление чисел посредством арабских цифр 0, 1,2, 3, 4, 5, 6, 7, 8, 9 - специальных знаков, используемых для записи чисел. Системы счисления различаются выбором базисных чисел и правилами образования из них остальных чисел.

Системы счисления, в которых любое число получается путем сложения или вычитания базисных чисел, называются аддитивными. При таком представлении чисел правила сложения для небольших чисел очевидны и просты, однако если возникает необходимость выполнять операции сложения над большими числами или операции умножения и деления, то «римская» система счисления оказывается неудобной.

В этой ситуации преимущественнее оказываются позиционные системы счисления.

Существуют позиционные и непозиционные системы счисления.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. В позиционной системе счисления представления чисел далеко не так просты и очевидны, как в «римской» системе счисления, систематичность представления, основанная на «позиционном весе» цифр, обеспечивает простоту выполнения операций умножения и деления.

В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. В «римской» системе счисления каждый числовой знак в записи любого числа имеет одно и то же значение, т.е. значение числового знака не зависит от его расположения в записи числа. В римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти, а I – это единица.

Для изображения чисел в настоящее время используются в основном позиционные системы счисления. Привычной для всех является десятичная система счисления. В этой системе для записи любых чисел используется только десять разных знаков (цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры введены для обозначения первых десяти последовательных чисел, а следующее число 10 и т.д. обозначается уже без использования новых цифр. Однако введением этого обозначения сделан важный шаг в построении системы счисления: значение каждой цифры поставлено в зависимость от того места, где она стоит в изображении числа.

Десятичная запись любого числа X в виде последовательности цифр: , основана на представлении этого числа в виде полинома:

,

где каждый коэффициент аi, может быть одним из чисел, для обозначения которых введены специальные знаки. Запись числа X в формуле представляет собой просто перечисление всех коэффициентов этого полинома. Точка, отделяющая целую часть числа от дробной, служит для фиксации конкретных значений каждой позиции в этой последовательности цифр и является началом отсчета.

Количество К различных цифр, употребляющихся в позиционной системе счисления, называется ее основанием системы счисления, а сама система счисления называется К-ичной. Например, основанием десятичной системы счисления является число 10; двоичной - число 2; троичной - число 3 и т.д. Для записи произвольного числа в K-ичной системе счисления достаточно иметь К разных цифр 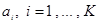. Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.

Запись произвольного числа X в K-ичной позиционной системе счисления основывается на представлении этого числа в виде полинома:

,

где каждый коэффициент а, может быть одним из базисных чисел и изображается одной цифрой. В качестве базисных чисел берутся последовательные целые числа от 0 до К-1 включительно.

Позиции цифры, отсчитанные от запятой (точки), отделяющей целую часть от дробной, называются разрядами. В позиционной системе счисления вес каждого разряда больше соседнего в число раз, равное основанию системы К.

Пример: Для десятичной системы счисления (основание К=10) имеем число 6321.564. Веса разряда и коэффициенты а для этого числа будут следующими:

Все известные позиционные системы счисления являются аддитивно-мультипликативными. Особенно отчетливо аддитивно-мультипликативный способ образования чисел из базисных выражен в числительных русского языка, например пятьсот шестьдесят восемь (т.е.5 сотен + 6 десятков + 8).

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами. Нужно только пользоваться теми таблицами сложения и умножения, которые имеют место при данном основании К системы счисления. Во всех позиционных системах счисления с любым основанием К умножения на числа вида Кm, где m - целое число, сводится просто к перенесению запятой у множимого на m разрядов вправо или влево (в зависимости от знака m), так же как и в десятичной системе.

Для указания того, в какой системе счисления записано число, условимся при его изображении основание системы счисления указывать в виде нижнего индекса при нем, например, 35,648 или подстрочным индексом, заключенным в круглые скобки, например: 1101(2).

В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.

Продвижением цифры называют замену её следующей по величине. Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.

Целые числа в любой системе счисления порождаются с помощью Правила счета:

Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.

В настоящее время в ЭВМ применяют двоичную, восьмеричную и шестнадцатеричную системы счисления.