Лекция 10. Критерии оптимальности

Наиболее эффективным способом исследования работоспособности сложного вычислительного/радиотехнического устройства является его моделирование. На сегодняшний день основными способами исследования работоспособности вычислительных устройств являются следующие: макетирование, физическое моделирование, аналитическое моделирование и математическое моделирование.

Натурное макетирование - один из наиболее старых способов проектирования РЭА. Его главное достоинство - максимальная достоверность результатов, обусловленная работой с реальными схемами, а не их приближенными моделями. Кроме того, макетирование характеризуется наглядностью получаемых результатов. В то же время макетирование имеет ряд крупных недостатков. Основные из них - высокая стоимость, длительность создания макета, ограничение возможности макетирования.

Физическое моделирование представляет собой исследование объектов одной физической природы с помощью объектов, имеющих другую физическую природу, но при этом одинаковое с исследуемыми объектами математическое описание. В основе физического моделирования лежит обычно принцип электрофизических аналогий. Он может применяться для изучения сопутствующих работе схем, например, тепловых процессов, математическое моделирование которых слишком сложно и трудоемко.

Аналитическое моделирование по заранее известным формулам или расчет по аналитическим выражениям выполняется с помощью формул, связывающих выходные параметры интегральных схем (функциональные и изменяемые) с внутренними параметрами, т.е. параметрами их отдельных компонентов. При этом делаются значительные упрощения. Например, экспоненциальные вольтамперные зависимости считаются линейными. Основные недостатки данного метода проектирования БИС - высокая трудоемкость вывода формул и, как правило, низкая точность расчетов. Основное достоинство - доступность.

Моделирования на компьютере предполагает использование в качестве объекта отладки программной модели проектируемой системы. Этот метод является универсальным в том смысле, что программная модель может быть получена для вычислительной системы любой структуры и архитектуры. Наиболее широко применяемым методом проектирования является математическое моделирование, под которым обычно понимается составление математической модели устройства и ее использованием на ЭВМ в процедурах расчета, анализа, оптимизации и синтеза.

Автоматизированное проектирование включает решение задач расчета, анализа, оптимизации и синтеза. Эти задачи называются проектными процедурами и имеют следующее содержание:

• расчет - определение выходных параметров и характеристик устройства при неизменных значениях его внутренних параметров и постоянной структуре;
• анализ - определение изменения выходных параметров и характеристик устройства в зависимости от изменения его внутренних и выходных параметров. В автоматизированном проектировании задача расчета часто называется одновариантным анализом, а задача синтеза - многовариантным анализом;
• оптимизация - определение наилучших в том или ином смысле значений выходных параметров и характеристик путем целенаправленного изменения внутренних параметров устройства. Это является содержанием параметрической оптимизации. Оптимизация структуры устройства является содержанием структурной оптимизации.

· В общем случае синтезом называется генерация исходного варианта устройства, включая его структуру при структурном синтезе и получение его внутренних параметров при параметрическом синтезе. Полученное в результате синтеза устройство не обязательно должно быть наилучшим, но обязательно работоспособным. В большинстве случаев устройство, полученное в результате синтеза, даже оптимального, требует доработки, чтобы удовлетворить многочисленным требованиям, учесть которые на стадии синтеза невозможно из-за их многообразия и сложности.

Реальный процесс автоматизированного проектирования РЭА обычно состоит из двух этапов:

1. Синтеза структуры и эскизного, обычно неавтоматизированного, по упрощенным формулам расчета ее параметров с целью получения работоспособного варианта РЭА, который будет играть роль начального приближения. Следует отметить, что в настоящее время ведутся работы по автоматизации и этого этапа проектирования.

2. Доводки полученного варианта до кондиций, соответствующих техническому заданию (ТЗ) с помощью оптимизации – параметрического синтеза.

Оптимизация как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Термином "оптимизация" в литературе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего или "оптимального" решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. Поэтому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.

Процедуры параметрического синтеза в САПР выполняются либо человеком в процессе многовариантного анализа (в интерактивном режиме), либо реализуются на базе формальных методов оптимизации (в автоматическом режиме). В последнем случае находят применение несколько постановок задач оптимизации.

 

А) детерминированная постановка: заданы условия работоспособности на выходные параметры и нужно найти номинальные значения проектных параметров , к которым относятся параметры всех или части элементов проектируемого объекта.

 

Б) стохастическая постановка - задача оптимизации, в которой критерий оптимальности 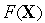и/или ограничивающие функции зависят от случайного вектора внешних параметров .

 

Проектные задачи являются многокритериальными, возникает проблема выбора критерия b сведения многокритериальной задачи к однокритериальной. Применяют несколько способов выбора критерия оптимальности. В частном критерии среди выходных параметров один выбирают в качестве целевой функции, а условия работоспособности остальных выходных параметров относят к ограничениям задачи (1).

 

Рис. 1. Области Парето и работоспособности

На этом рисунке представлено двумерное пространство выходных параметров и , для которых заданы условия работоспособности и . Кривая является границей достижимых значений выходных параметров. Это ограничение объективное и связано с существующими физическими и технологическими условиями производства, называемыми условиями реализуемости. Область, в пределах которой выполняются все условия реализуемости и работоспособности, называют областью работоспособности. Множество точек пространства выходных параметров, из которых невозможно перемещение, приводящее к улучшению всех выходных параметров, называют областью компромиссов, или областью Парето. Участок кривой (см. рис. 1) относится к области Парето.

 

 

Аддитивный критерий объединяет (свертывает) все выходные параметры (частные критерии) в одну целевую функцию, представляющую собой взвешенную сумму частных критериев

(2)

где — весовой коэффициент, 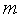— число выходных параметров. Функция (2) подлежит минимизации, при этом если условие работоспособности имеет вид , то .

Недостатки аддитивного критерия — субъективный подход к выбору весовых коэффициентов и неучет требований ТЗ.

Аналогичные недостатки присущи и мультипликативному критерию, целевая функция которого имеет вид

(3)

Нетрудно видеть, что если прологарифмировать (3), то мультипликативный критерий превращается в аддитивный.

Более предпочтительным является максиминный критерий, в качестве целевой функции которого принимают выходной параметр, наиболее неблагополучный с позиций выполнения условий работоспособности. Например, по всем параметрам имеется 50% запас, а по одному -10%. Расчет ведется по достижению максимума этого параметра, например 30% при допустимых запасах остальных параметров.

В математическом программировании базовая задача оптимизации ставится как задача определение экстремума

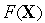где — целевая функция, — вектор управляемых (проектных) параметров, и — функции-ограничения, — допустимая область в пространстве управляемых параметров.

(1)

 

Запись (1) интерпретируется как задача поиска экстремума целевой функции путем варьирования управляемых параметров в пределах допустимой области.

Таким образом, для выполнения расчета номинальных значений параметров необходимо, во-первых, сформулировать задачу в виде (1), во-вторых, решить задачу поиска экстремума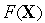

 

 

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: