 |
Подходы к решению задач структурного синтеза
|
|
|
|
Задачи синтеза структур проектируемых объектов относятся к наиболее трудно формализуемым. Существует ряд общих подходов к постановке этих задач, однако практическая реализация большинства из них неочевидна. Структурный синтез, как правило, выполняют в интерактивном режиме при решающей роли инженера-разработчика, а ЭВМ играет вспомогательную роль: предоставление необходимых справочных данных, фиксация и оценка промежуточных и окончательных результатов.
Задачу принятия решений (ЗПР) формулируют следующим образом:
где 
— множество альтернатив проектного решения (морфологическое множество), 
— множество критериев (выходных параметров), по которым оценивается соответствие альтернативы поставленным целям; 
— модель, позволяющая для каждой альтернативы рассчитать вектор критериев при условии 
, 
— решающее правило для выбора наиболее подходящей альтернативы в многокритериальной ситуации.
Простейший способ задания множества — явное перечисление всех альтернатив. Каждой альтернативе в информационно-поисковой системе ИПС соответствует поисковый образ, состоящий из значений атрибутов 
и ключевых слов вербальных характеристик.
Явное перечисление альтернатив при представлении множества альтернатив возможно лишь при малой мощности . Поэтому в большинстве случаев используют неявное описание в виде способа (алгоритма или набора правил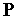 
) синтеза проектных решений из ограниченного набора элементов 
. Поэтому здесь 
, а типичный процесс синтеза проектных решений состоит из следующих этапов:
1. формирование альтернативы 
(это может быть выбор из базы данных ИПС по сформированному поисковому предписанию или генерация из в соответствии с правилами );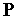
|
|
|
2. оценка альтернативы по результатам моделирования с помощью модели;
3. принятие решения относительно перехода к следующей альтернативе или прекращения поиска (выполняется лицом, принимающим решение или автоматически).
Для описания множеств набора правил 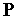и набора элементов используют следующие подходы.
· морфологические таблицы и альтернативные И-ИЛИ-деревья;
· представление знаний в интеллектуальных системах — фреймы, семантические сети, продукции;
· генетические методы;
· базы физических эффектов и эвристических приемов, применяемые при решении задач изобретательского характера.
Морфологическая таблица (
) представляет собой обобщенную структуру в виде множества функций, выполняемых компонентами синтезируемых объектов рассматриваемого класса, и подмножеств способов их реализации. Каждой функции можно поставить в соответствие одну строку таблицы, каждому способу ее реализации — одну клетку в этой строке. Следовательно, в морфологических таблицах элемент 
означает 
-й вариант реализации 
-й функции в классе технических объектов, описываемом матрицей . Морфологические таблицы считают средством неавтоматизированного синтеза, помогающим человеку просматривать компактно представленные альтернативы, преодолевать психологическую инерцию. Последнее связано с тем, что внимание человека, принимающего решения обращается на варианты, которые без морфологической таблицы оставались бы вне его поля зрения.
Любую морфологическую таблицу можно представить в виде дерева. В общем случае разные функции могут быть реализованы одними и теми же способами, тогда вместо дерева имеем граф, называемый И-ИЛИ-графом (или альтернативным графом).
Каждая И вершина дерева соответствует частной морфологической таблице, т.е. множеству функций так, что -я выходящая ветвь отображает -ю функцию. Каждая ИЛИ вершина, инцидентная -й ветви, соответствует множеству вариантов реализации -й функции, при этом -я исходящая из ИЛИ вершины ветвь отображает -й вариант реализации.
|
|
|
Трудности эффективного решения задачи существенно возрастают при наличии ограничений, типичными среди которых являются ограничения на совместимость способов реализации разных функций, т.е. ограничения вида
| (1) |
где 
, если в оцениваемый вариант вошел элемент 
, иначе 
.
Условие (1) означает, что в допустимую структуру не могут входить одновременно элементы и 
. Совокупность ограничений типа (1) можно представить как систему логических уравнений с неизвестными 
. Тогда задачу синтеза можно решать эволюционными методами, если предварительно или одновременно с ней решать систему логических уравнений (задачу о выполнимости).
Стремление к сокращению перебора решений, составляют операции разделения множества вариантов на подмножества и отсечения неперспективных подмножеств. Эти методы объединяются под названием метода ветвей и границ. Основная разновидность метода ветвей и границ относится к точным методам решения комбинаторных задач. Смысл метода в ветвлении множества М на подмножества, вычисление в каждом границ, например, нижних, сортировка подмножеств с наиболее интересными результатами и снова ветвление…
Сущность метода распространения ограничений заключается в сужении допустимых интервалов управляемых переменных 
с помощью учета (распространения) исходных ограничений на выходные параметры 
и 
.
Для пояснения метода рассмотрим простой пример. Пусть в задаче фигурируют три управляемых целочисленных переменных 
, 
, 
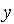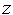, заданы исходные интервалы допустимых значений этих переменных 
, 
, 
, а область 
определена ограничениями
| (1) |
| (2) |
Распространение ограничения (1) на интервал переменной 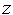приводит к уменьшению его верхней границы, так как 
, а с учетом ограничения (2) — к ее новой корректировке 
, так как 
, а также к увеличению нижних границ переменных и 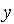, так как решение неравенств 
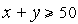и (2) дает 
, 
. Таким образом, получено сужение допустимой области 
, 
, 
.
Метод легко распространяется на задачи с нечисловыми параметрами. В этом случае вместо сокращения числовых интервалов уменьшают мощности допустимых подмножеств значений параметров.
|
|
|
На базе метода распространения ограничений компанией ILOG создан программный комплекс оптимизации и синтеза проектных решений, состоящий из подсистем Solver, Configurator, Scheduler и др. Основной продукт - ILOG Solver. ILOG Solver поддерживает работу с целыми, вещественными, логическими и множественными переменными и позволяет использовать линейные, нелинейные и логические ограничения. В ILOG Solver реализовано несколько эффективных алгоритмов поиска, включающих как стандартные стратегии (поиск в глубину, поиск сначала наилучшего), так и специализированные алгоритмы для задач удовлетворения ограничения над конечными областями.
|
|
|
