 |
Методы одномерной оптимизации
|
|
|
|
Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:
f(x) -> min, x принадлежит [a, b].
Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию f(x) унимодальной на отрезке [a, b]
т.е. на котором имеется один минимум.
К методам одномерной оптимизации относятся методы равномерного поиска, дихотомического деления, золотого сечения, чисел Фибоначчи, полиномиальной аппроксимации и ряд их модификаций.
Метод перебора или равномерного поиска является простейшим из прямых методов минимизации и состоит в следующем.
Разобьем отрезок [a,b] на n равных частей точками деления:
xi=a+i(b-a)/n, i=0,...n
Вычислив значения F(x) в точках xi, путем сравнения найдем точку xm, где m - это число от 0 до n, такую, что
F(xm) = min F(xi) для всех i от 0 до n.
Погрешность определения точки минимума xm функции F(x) методом перебора не превосходит величены Eps=(b-a)/n.
Согласно методу дихотомического деления (рис. 3,а) отрезок делят пополам и в точках, отстоящих от центра  отрезка на величину допустимой погрешности
отрезка на величину допустимой погрешности 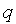 , рассчитывают значения целевой функции
, рассчитывают значения целевой функции  и
и  . Если окажется, что
. Если окажется, что  , то минимум находится на отрезке
, то минимум находится на отрезке  , если
, если  , то минимум — на
, то минимум — на  , если
, если 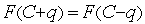 — на
— на  . Таким образом, на следующем шаге вместо отрезка
. Таким образом, на следующем шаге вместо отрезка 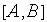 нужно исследовать суженный отрезок
нужно исследовать суженный отрезок  ,
,  или
или  . Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности
. Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности 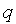 . Таким образом, требуется не более
. Таким образом, требуется не более 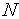 шагов, где
шагов, где 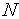 — ближайшее к
— ближайшее к 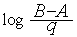 целое значение, но на каждом шаге целевую функцию следует вычислять дважды.
целое значение, но на каждом шаге целевую функцию следует вычислять дважды.
|
|
|

|
Рис. 3. Одномерная минимизация: а — дихотомическое деление; б — золотое сечение
Золотое сечение (золотая пропорция) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью
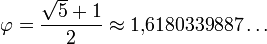
и, наоборот, отношение меньшей части к большей

Геометрическое построение. Золотое сечение отрезка AB можно построить следующим образом: в точке B восстанавливают перпендикуляр к AB, откладывают на нём отрезок BC, равный половине AB, на отрезке AC откладывают отрезок AD, равный AC − CB, и наконец, на отрезке AB откладывают отрезок AE, равный AD. Тогда


Рассмотрим для простоты отрезок [0,1] единичной длины.

Ясно, что на отрезке имеется две таких точки 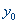 и
и  , они симметричны относительно концов. Точка
, они симметричны относительно концов. Точка 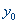 производит золотое сечение отрезка [A,C], а точка
производит золотое сечение отрезка [A,C], а точка  производит золотое сечение отрезка [B,D]. Положим |AB|= x. Тогда |BD|=1-x. В соответствии с определением точки «золотого сечения» имеем:
производит золотое сечение отрезка [B,D]. Положим |AB|= x. Тогда |BD|=1-x. В соответствии с определением точки «золотого сечения» имеем:  . Решив эту пропорцию, получим
. Решив эту пропорцию, получим  .
.
Таким образом, требуется не более 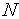 шагов и
шагов и  вычисление целевой функции, где
вычисление целевой функции, где 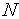 можно рассчитать, используя соотношение
можно рассчитать, используя соотношение 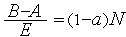 при заданной погрешности
при заданной погрешности 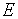 определения экстремума.
определения экстремума.
Согласно методу чисел Фибоначчи, используют числа Фибоначчи 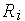 , последовательность которых образуется по правилу
, последовательность которых образуется по правилу  при
при 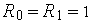 , т.е. ряд чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,... Метод аналогичен методу золотого сечения с тем отличием, что коэффициент «а» равен отношению
, т.е. ряд чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,... Метод аналогичен методу золотого сечения с тем отличием, что коэффициент «а» равен отношению  , начальное значение
, начальное значение  определяется из условия, что
определяется из условия, что 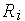 должно быть наименьшим числом Фибоначчи, превышающим величину
должно быть наименьшим числом Фибоначчи, превышающим величину  , где
, где 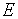 — заданная допустимая погрешность определения экстремума. Так, если
— заданная допустимая погрешность определения экстремума. Так, если  , то начальное значение
, то начальное значение  , поскольку
, поскольку  , и
, и 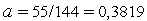 , на следующем шаге будет
, на следующем шаге будет  и т.д.
и т.д.
Метод полиномиальной аппроксимации: P = a0+a1 x +a2 x2
|
|
|
Выбирают промежуточную точку С на отрезке А,В и записывают значения целевой функции в каждой точке. Далее решают систему из трех АУ, полученных подстановкой P(x) и А, В, С вместо х – получают аi. Исходя из (dP(x)/dx =0) определяют точку экстремума.
Сравнение эффективности алгоритмов одномерной условной оптимизации.
Аналитическое решение возможнотолько при условии одномерной унимодальной функции Ф(х) на интервале <а, b>. В качестве критерия используют максимальную длину текущего интервала неопределенности (ТИН) после N испытаний.
А) после одной итерации равномерного поиска ТИН уменьшается в N/2 раз
W=(b-a)/N/2
Б) при дихотомическом поиске после одной итерации ТИН уменьшается в 2 раза
W= (b-a)/2n
B) алгоритм Фибоначчи: i-число Фибоначчи, N-шаг. W= (b-a)/i(N).
В результате:
-при 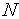 =14 алгоритм Фибоначчи почти в 3 раз эффективнее алгоритма деления пополам.
=14 алгоритм Фибоначчи почти в 3 раз эффективнее алгоритма деления пополам.
-при 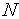 =14 алгоритм золотого сечения примерно на 40 процентов эффективнее алгоритма Фибоначчи.
=14 алгоритм золотого сечения примерно на 40 процентов эффективнее алгоритма Фибоначчи.
http://optimizaciya-sapr.narod.ru/map.html
|
|
|


