Методы поиска условных экстремумов

Метод множителей Лагранжа, ориентирован на поиск экстремума при наличии ограничений типа равенств 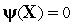, т.е. на решение задачи

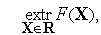
(1)

где .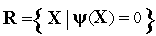

Суть метода заключается в преобразовании задачи условной оптимизации (1) в задачу безусловной оптимизации с помощью образования новой целевой функции

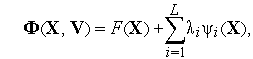
где 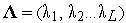— вектор множителей Лагранжа, — число ограничений. Необходимые условия экстремума функции :

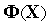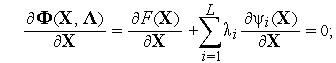
(2)

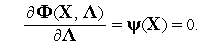
Система (2) содержит 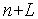алгебраических уравнений, где 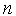— размерность пространства управляемых параметров, ее решение дает искомые координаты экстремальной точки и значения множителей Лагранжа. Однако при численном решении (2), что имеет место при использовании алгоритмических моделей, возникают те же трудности, что и в методе Ньютона. Поэтому в САПР основными методами решения задач математического программирования (ЗМП) являются методы штрафных функций и проекции градиента.

Основная идея методов штрафных функций — преобразование задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции 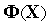введением в исходную целевую функцию 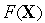специальным образом выбранной функции штрафа :

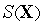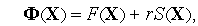
где — множитель, значения которого можно изменять в процессе оптимизации.

Функция штрафа обеспечивает появления барьера у целевой функции и соотношение между условным в точке и безусловным в точке 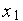минимумами 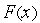. Штрафная функция не единственна. Обычно она стремится в бесконечности в точках, где ограничения не выполняются и равно 0 во всех остальных точках. В одномерном случае ситуация иллюстрируется рис. 10.

Функция 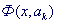называется штрафной функцией множества G, если для любых параметров

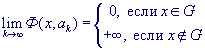
Таким образом, задача условной минимизации f (x) заменяется последовательностью задач безусловной минимизации 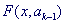при k =1,2,.... При этом, исходя из заданной начальной точки x0, находится последовательность точек 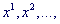сходящаяся при определенных условиях к решению исходной задачи. В зависимости от вида Ф(х, а) различают методы внешних штрафных функций и методы внутренних штрафных функций или барьерных функций.

На рис.- внутренние щтрафные функции.

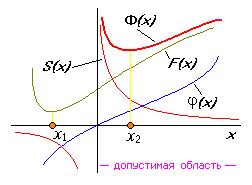
Рис. 10. Метод штрафных функций

Основной вариант метода проекции градиента ориентирован на задачи математического программирования c ограничениями типа равенств.

Поиск при выполнении ограничений осуществляется в подпространстве измерений, где 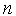— число управляемых параметров, 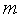— число ограничений, при этом движение осуществляется в направлении проекции градиента целевой функции 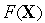на гиперплоскость, касательную к гиперповерхности ограничений (точнее к гиперповерхности пересечения гиперповерхностей ограничений).

Поиск минимума начинают со спуска из исходной точки на гиперповерхность ограничений. Далее выполняют шаг в указанном выше направлении (шаг вдоль гиперповерхности ограничений). Поскольку этот шаг может привести к заметному нарушению ограничений, вновь повторяют спуск на гиперповерхность ограничений и т.д. Другими словами, поиск заключается в выполнении пар шагов, каждая пара включает спуск на гиперповерхность ограничений и движение вдоль гиперповерхности ограничений.

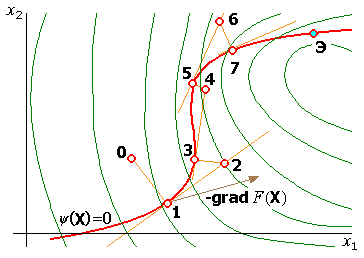
Идею метода легко пояснить для случая поиска в двумерном пространстве при одном ограничении 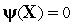. На рис. 11 это ограничение представлено жирной линией, а целевая функция — совокупностью более тонких линий равного уровня. Спуск обычно осуществляют по нормали к гиперповерхности ограничений (в данном случае к линии ограничения). Условие окончания поиска основано на сопоставлении значений целевой функции в двух последовательных точках, получаемых после спуска на гиперповерхность ограничений.

Рис. 11. Траектория поиска в соответствии с методом проекции градиента