 |
Методы безусловной минимизации функций многих переменных
|
|
|
|
Задача безусловной оптимизации состоит в нахождении минимума или максимума функции в отсутствие каких-либо ограничений. Несмотря на то, что большинство практических задач оптимизации содержит ограничения, изучение методов безусловной оптимизации важно с нескольких точек зрения. Многие алгоритмы решения задачи с ограничениями предполагают сведение ее к последовательности задач безусловной оптимизации. Другой класс методов основан на поиске подходящего направления и последующей минимизации вдоль этого направления.
Среди методов оптимизации нулевого порядка в САПР находят применение методы Розенброка, конфигураций, деформируемого многогранника, случайного поиска.
К методам с использованием производных относятся методы наискорейшего спуска, сопряженных градиентов, переменной метрики.
Метод покоординатного спуска характеризуется выбором направлений поиска поочередно вдоль всех 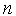 координатных осей, шаг рассчитывается на основе одномерной оптимизации, критерий окончания поиска
координатных осей, шаг рассчитывается на основе одномерной оптимизации, критерий окончания поиска 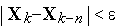 , где
, где  — заданная точность определения локального экстремума,
— заданная точность определения локального экстремума, 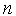 — размерность пространства управляемых параметров. Траектория покоординатного спуска для примера двумерного пространства управляемых параметров показана на рис. 4, где
— размерность пространства управляемых параметров. Траектория покоординатного спуска для примера двумерного пространства управляемых параметров показана на рис. 4, где 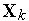 — точки на траектории поиска,
— точки на траектории поиска,  — управляемые параметры. Целевая функция представлена своими линиями равного уровня, около каждой линии записано соответствующее ей значение
— управляемые параметры. Целевая функция представлена своими линиями равного уровня, около каждой линии записано соответствующее ей значение 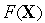 . Очевидно, что
. Очевидно, что  есть точка минимума.
есть точка минимума.

|
Рис. 4. Траектория покоординатного спуска
При использовании метода покоординатного спуска велика вероятность "застревания" поиска на дне оврага вдали от точки экстремума. На рис. 5 видно, что после попадания в точку  , расположенную на дне оврага, дальнейшие шаги возможны лишь в направлениях
, расположенную на дне оврага, дальнейшие шаги возможны лишь в направлениях 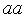 или
или  , но они приводят к ухудшению целевой функции. Следовательно, поиск прекращается в точке
, но они приводят к ухудшению целевой функции. Следовательно, поиск прекращается в точке 
|
|
|
Примечание. Оврагом называют часть пространства управляемых параметров, в которой наблюдаются слабые изменения производных целевой функции по одним направлениям и значительные изменения с переменой знака — по некоторым другим направлениям. Знак производной меняется в точках, принадлежащих дну оврага.

|
Рис. 5. "Застревание" покоординатного спуска на дне оврага
В то же время при благоприятной ориентации дна оврага, а именно при положении одной из координатных осей, близком к параллельности с дном оврага, поиск оказывается весьма быстрым. Эта ситуация показана на рис. 6.

|
Рис. 6. Траектория покоординатного спуска при благоприятной ориентации координатных осей
Метод Розенброка заключается в таком повороте координатных осей, чтобы одна из них оказалась квазипараллельной дну оврага. Такой поворот осуществляют на основе данных, полученных после серии из 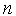 шагов покоординатного спуска. Положение новых осей
шагов покоординатного спуска. Положение новых осей  может быть получено линейным преобразованием прежних осей
может быть получено линейным преобразованием прежних осей  : ось
: ось  совпадает по направлению с вектором
совпадает по направлению с вектором 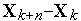 ; остальные оси выбирают из условия ортогональности к
; остальные оси выбирают из условия ортогональности к  и друг к другу.
и друг к другу.
Другой удачной модификацией покоординатного спуска является метод конфигураций (Хука-Дживса). В соответствии с этим методом вначале выполняют обычную серию из 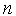 шагов покоординатного спуска, затем делают дополнительный шаг в направлении вектора
шагов покоординатного спуска, затем делают дополнительный шаг в направлении вектора  , как показано на рис. 7, где дополнительный шаг выполняют в направлении вектора
, как показано на рис. 7, где дополнительный шаг выполняют в направлении вектора  , что и приводит в точку
, что и приводит в точку 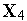 .
.

|
Рис. 7. Иллюстрация метода конфигураций
Поиск экстремума методом деформируемого многогранника (Нелдера-Мида) основан на построении многогранника с  вершинами на каждом шаге поиска, где
вершинами на каждом шаге поиска, где 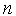 — размерность пространства управляемых параметров. В начале поиска эти вершины выбирают произвольно, на последующих шагах выбор подчинен правилам метода.
— размерность пространства управляемых параметров. В начале поиска эти вершины выбирают произвольно, на последующих шагах выбор подчинен правилам метода.
|
|
|
Эти правила поясняются рис. 8 на примере двумерной задачи оптимизации. Выбраны вершины исходного треугольника:  ,
,  ,
, 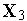 . Новая вершина
. Новая вершина 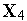 находится на луче, проведенном из худшей вершины
находится на луче, проведенном из худшей вершины  (из вершины с наибольшим значением целевой функции) через центр тяжести
(из вершины с наибольшим значением целевой функции) через центр тяжести 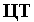 многогранника, причем рекомендуется
многогранника, причем рекомендуется 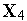 выбирать на расстоянии
выбирать на расстоянии  от
от 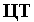 , равном
, равном  . Новая вершина
. Новая вершина 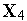 заменяет худшую вершину
заменяет худшую вершину  . Если оказывается, что
. Если оказывается, что 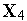 имеет лучшее значение целевой функции среди вершин многогранника, то расстояние
имеет лучшее значение целевой функции среди вершин многогранника, то расстояние  увеличивают. На рисунке именно эта ситуация имеет место и увеличение
увеличивают. На рисунке именно эта ситуация имеет место и увеличение  дает точку
дает точку  . В новом многограннике с вершинами
. В новом многограннике с вершинами  ,
, 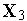 ,
,  худшей является вершина
худшей является вершина  , аналогично получают вершину
, аналогично получают вершину  , затем вершину
, затем вершину  и т.д. Если новая вершина окажется худшей, то в многограннике нужно сохранить лучшую вершину, а длины всех ребер уменьшить, например вдвое (стягивание многогранника к лучшей вершине). Поиск прекращается при выполнении условия уменьшения размеров многогранника до некоторого предела.
и т.д. Если новая вершина окажется худшей, то в многограннике нужно сохранить лучшую вершину, а длины всех ребер уменьшить, например вдвое (стягивание многогранника к лучшей вершине). Поиск прекращается при выполнении условия уменьшения размеров многогранника до некоторого предела.
Методы случайного поиска, приведенные выше, характеризуются тем, что направления поиска  выбирают случайным образом.
выбирают случайным образом.

|
Рис. 8. Иллюстрация метода деформируемого многогранника
Особенностью метода наискорейшего спуска является выполнение шагов поиска в градиентном направлении

| (1) |
шаг  выбирается оптимальным с помощью одномерной оптимизации.
выбирается оптимальным с помощью одномерной оптимизации.
При использовании метода наискорейшего спуска, как и большинства других методов, эффективность поиска существенно снижается в овражных ситуациях.
Метод Ньютона основан на использовании необходимых условий безусловного экстремума целевой функции 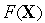

| (9) |
Выражение (9) представляет собой систему алгебраических уравнений, для решения которой можно применить известный численный метод решения СЛАУ, называемый методом Ньютона. Корень системы (9) есть стационарная точка, т.е. возможное решение экстремальной задачи. Метод Ньютона является итерационным, он основан на линеаризации (9) в окрестности текущей точки поиска 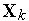
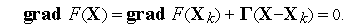 , где Г - матрица вторых частных производных целевой функции по управляемым параметрам. , где Г - матрица вторых частных производных целевой функции по управляемым параметрам.
| (10) |
Выражение (10) — это система линейных алгебраических уравнений. Ее корень есть очередное приближение 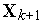 к решению
к решению

|
|
|
Если процесс сходится, то решение достигается за малое число итераций, окончанием которых служит выполнение условия

Главный недостаток метода — высокая трудоемкость вычисления и обращения матрицы  , к тому же ее вычисление численным дифференцированием сопровождается заметными погрешностями, что снижает скорость сходимости.
, к тому же ее вычисление численным дифференцированием сопровождается заметными погрешностями, что снижает скорость сходимости.
В методе переменной метрики вместо трудно вычисляемой обратной матрицы Гессе Г-1 используют некоторую более легко вычисляемую матрицу  , т.е.
, т.е.
 Матрицу
Матрицу  корректируют на каждом шаге, т.е.
корректируют на каждом шаге, т.е.

где

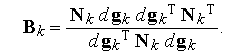


Поэтому
 ,
, 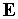 — единичная матрица. Начальное значение матрицы
— единичная матрица. Начальное значение матрицы 
Можно показать, что  стремится к
стремится к  ,
,  — к
— к 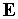 при
при  , где
, где 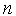 — размерность пространства управляемых параметров.
— размерность пространства управляемых параметров.
|
|
|


