Определение численности исполнителей

Данные анализа трудозатрат проекта необходимо использовать для определения численности исполнителей проекта.

Средняя численность исполнителей при реализации отдельных этапов проекта можно определить, используя соотношение 13:

13

где, - затраты труда на выполнение соответствующего этапа (задачи) проекта,

F - фонд рабочего времени.

Величина фонда рабочего времени определяется соотношением 14:

14

где, Т - время выполнения проекта в месяцах,

F_M - фонд времени в текущем месяце, который рассчитывается из учета общества числа дней в году, числа выходных и праздничных дней (15):

15

где, t_p - продолжительность рабочего дня,

D_K - общее число дней в году,

D_B - число выходных дней в году,

D_П - число праздничных дней в году.

Подставляя результат вычислений формулы 15 в соотношение 14, и, далее, в соотношение 13, округляют результат до большего целого и получают среднее число необходимых исполнителей проекта.

Продолжительность отдельных работ при одновременном выполнении их несколькими исполнителями (t_i)определяется из соотношения 16:

16

где, t_pp - расчетная продолжительность работы,

W_исп - количество исполнителей,

К_Н - коэффициент выполнения нормы.

Продолжительность работ следует рассчитывать исходя из того, что одной работой занят один исполнитель, а коэффициент выполнения нормы равен единице (обычно он составляет 1,0 - 1,2).

Затраты труда по отдельным работам, полученные с помощью соотношения 16, следует занести в таблицу 2. Для этого следует добавить справа дополнительный столбец «Количество исполнителей».

Рассмотрим следующий пример. Необходимо определить число исполнителей, которые смогут выполнить проект, трудоемкость которого состав 878 час. в течении трех месяцев.

Для определения числа исполнителей, сначала, следует определить фонд времени в текущем месяце, который может составить = 168 часов.

Фонд рабочего времени для трех месяцев определится в объеме: 3×168 = 504 часа, Тогда, средняя численность исполнителей проекта определится значением: .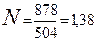

Таким образом, для реализации данного проекта необходимо привлечь двух исполнителей.

 

Сетевая модель проекта

Сетевой график устанавливает взаимосвязь между всеми работами проекта и позволяет определить продолжительность как отдельных этапов, так и всего проекта в целом.

№	Событие	Код работы	Работа	(ч-часы) (ч.-дни)
	Начало работ	0-1	Разработка структуры. данных	118,4	14,8
	Структура данных	1-2	Разработка модуля
		1-6	Создание структуры данных
	Основной модуль	2-3	Методика тестирования
		3-8	Создание основного модуля
…	…	…	…	…	…

Рис. 2.3. Фрагмент таблицы основных событий и работ проекта

Построение сетевого графика предполагает использование метода сетевого планирования, на базе которого разрабатывается информационно-динамическая модель процесса выполнения проекта. Построение сетевой модели включает оценку степени детализации комплекса работ, определения логической связи между отдельными работами и временные характеристики выполнения этапов проекта

В сетевой модели выделяют события и работы. В качестве событий, например, принимают факты начала проекта, окончания разработки отдельных модулей, интерфейсов, выполнения отладки и т.п. Все события нумеруются по порядку от исходного к завершающему, как показано на рис. 2.3.

В процессе достижения каждого события реализуется определенная последовательность работ, например: процесс разработки конкретного модуля, сборка программы, оформление документации и т.п. Конечным событием является выполнение всего проекта по разработке ПО. Каждой работе присваивается "Код работы", состоящий из номера наступившего события и номера того события, которое достигается в результате выполнения данной работы, например, для рис. 2, если 0 - начало проекта, а 1 - событие "разработка структуры данных завершена", то 0-1 - определяет работу по разработке структуры данных. В качестве работы может выступать и "фиктивная работа", которая определяет ожидание окончания связанных работ и длительность которой равна 0 человеко-дней. Кодовые номера работ каждого этапа указываются в соответствующем блоке строк, относящегося к этому этапу, как показано в таблице на рис. 3.

Графическое отображение сетевой модели (сетевой график) содержит окружности, отображающие основные события проекта, и векторы, соединяющие эти окружности и определяющие необходимость выполнения соответствующих работ. Реальные работы изображаются сплошной линией, фиктивные - штриховой, а работы, лежащие на критическом пути - линией двойной толщины (рис. 6).

Окружности разделены на четыре сектора, в каждом из которых показаны номер данного события (в нижнем секторе), значение раннего срока наступления текущего события (в левом секторе), значение резерва времени текущего события (в верхнем секторе) и значение позднего срока наступления события (в правом секторе), как показано на рис. 2.4.

Рис. 2.4. Обозначение основных элементов сетевого графика: N_i, N_j - номер события, T_i^P - ранний срок наступления события i, T_i^п - поздний срок наступления события i, R_i - резерв времени события i, t_i,j - продолжительность работы i-j, R_ij^п - полный резерв времени работы i-j, R_ij^c - свободный резерв времени работы i-j.

Результаты расчета параметров сетевого графика сводят в таблицу, фрагмент которой показан на рис. 2.5.

№ События	Ранний срок наступления, Тр, часов	Поздний срок наступления, Тп, часов	Резерв времени события, Трез, часов
…	…	…	…

Рис. 2.5: Фрагмент таблицы сроков наступления и резервы времени событий.

 

В соответствии с содержанием таблицы основных событий и работ проекта строится графическая модель сетевого графика, пример которой показан на рис. 2.6. На соответствующих сегментах окружностей следует записать номера событий, а на векторах - продолжительность работ.

После построения графической модели следует рассчитать оставшиеся параметры элементов сети: сроки наступления событий, резервы времени, полный и свободный резервы времени.

Рис. 2.6. Отображение событий и работ на сетевом графике.

Ранний срок совершения события определяет минимальное время, необходимое для выполнения всех работ, предшествующих данному событию. Он равен продолжительности наибольшего из путей, ведущих от исходного события (0) к рассматриваемому и рассчитывается по соотношению 17:

17

Критический путь - максимальный путь от исходного события (0) до завершения проекта. Его определение позволяет обратить внимание на перечень событий, совокупность которых имеет нулевой резерв времени (рис. 2.6).

Все события в сети, не принадлежащие критическому пути, имеют резерв времени R_i, показывающий на какой предельный срок можно задержать наступление этого события, не увеличивая сроки окончания работ (т.е. продолжительности критического пути).

Поздний срок совершения события - максимально допустимое время наступления данного события, при котором сохраняется возможность соблюдения ранних сроков наступления последующих событий. Поздние сроки вычисляются, начиная с последнего события - завершения проекта, по критическому пути (т.е. справа налево по графику). Они равны разности между поздним сроком совершения j-го события и продолжительностью i-j работы. Поздний срок определяется соотношением 18:

18

Резерв времени события определяется следующим образом:

19

Полный резерв времени работы следует определить, используя соотношение 20:

20

Свободный резерв времени можно определить, применяя соотношение 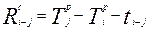21:

21

Так, например, для рассматриваемого проекта, значение трудозатрат которого приведены на рис. 5, определяют критический путь на сетевом графике - путь, проходящий через события с нулевым резервом времени и имеющий наибольшую длительность. Для сетевого графика, изображенного на рис. 6 критический путь проходит через события 0®1® 2® 3® 5® 6® 8® 11® 13® 14® 16. Длина критического пути в этом случае составляет 327 часов или 40,7 рабочих дней.

Сетевой график может иметь различный вид, важно, чтобы он ясно показывал взаимозависимость выполнения различных работ проекта и позволял определить критический путь. На рис. 7 показан один из вариантов сетевого графика, отражающих процесс проектирования, показанный в таблице 2.

Рис. 2.7: Вариант сетевого графика проекта.

Критический путь, полученный на сетевом графике (рис. 2.7) при условии, что одну работу выполняет один человек оказывается следующим: 0–1–2–3–4–8–10–12-13. В этом случае длина критического пути составит Tкр = 253 дня.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: