Может ли наиб вероятное число успехов в схеме Бернулли отличаться от мат ожидания числа успехов на 2?

По схеме Бернулли наиб вероятное число успехов: k=np+p. Мат. ожидания: так как схему Бернулли можно представить как биноминальное распределение M(x)=np, np+p-np=p Следоват, в схеме Бернулли наиб вероятное число успехов может отличаться от мат. ожидания на число р – Р успеха и известно, что p+q=1, p=1-q p<1. А значит отличаться на 2 не может.

35. локальная приближ формула Лапласа, основные свойства функции Гаусса ϕ (x) и укажите ее график. При каких условиях данная формула дает хорошее приближение? Какие условия применимости отличают эту формулу от приближенной формулы Пуассона?

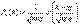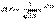Если n – велико, а р – отлично от 0 и 1, то где - функция Гаусса. Св-ва: а) . б) при больших верно 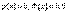. График Гаусса – нормальная кривая . Теоремы Лапласа дают удовлетворительное приближение при 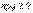. чем ближе значения p,q к 0,5, тем точнее данные формулы.

37. Укажите выражение для функции Лапласа Ф(x). Докажите нечётность функции Ф(x) и нарисуйте график y=Ф(x). Чему равно Ф(12)?

Функция: Ф(x) = 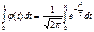. Док-во Ф(-x) = -Ф(x): запишем выражение Ф(-x) = 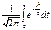и выполним замену z=-t, dz=-dt, при этом нижний предел интегрирования не изменится, а верхний станет равным x. Таким образом, Ф(-x) = 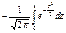= -Ф(x). График: симметричен относительно начала координат, проходит через (0;0). Горизонтальные асимптоты: -0,5 и 0,5. Ф(12) = 0,5.

 

Используя интегральную приближ формулу Лапласа, выведите формулу для оценки отклонения относит частоты соб А от p наступления A в одном опыте.

В условиях схемы Бернулли с заданными значениями n и p для данного e>0 оценим Р соб 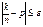, где k – число успехов в n опытах. Это нер-во эквивалентно |k-np|£en, т.е. -en £ k-np £ en или np-en £ k £ np+en. Таким образом, речь идёт о получении оценки для Р соб k₁ £ k £ k₂, где k₁ = np-en, k₂ = np+en. Применяя интеграл приближ формулу Лапласа, получим:P(» 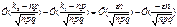. С учётом нечётности функции Лапласа получаем приближ рав-во P(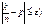» 2Ф(. Примечание: т.к. по условию n=1, то подставляем вместо n 1 и получаем окончат ответ.

 

Сформулируйте и докажите предельную теорему Пуассона.

При n®¥, p®0 b, а величина l = np остаётся постоянной 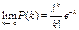. Док-во: имеем: 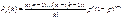, и т.к p=l/n, то 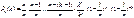. Выражение 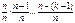- произведение k множителей, стремящихся к 1; поэтому и всё произведение стремится к 1. Выражение 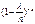стремится к 1. Что касается выражения 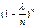, то его можно записать в виде 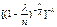. Замечая, что выражение в квадратных скобках имеет пределом число 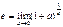, получим окончат: 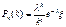, где x®1. Следует,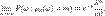

 

Запишите приближ формулы Пуассона. При каких условиях они дают хорошее приближение? Приведите примеры их применения.

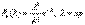– среднее число появлений события в n испытаниях. дает удовлетвор приближение для 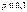и 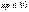.При больших np рекомендуется применять формулы Лапласа.Cоб, для кот применима формула Пуассона-редкие,т.к. Р их осуществления очень мала (0,001-0,0001). Пример: в тесто засыпают большое кол-во изюма (например, 10000 изюмин) и нужно оценить Р того, что в случ выбранной булке, испечённой из этого теста, окажется, к примеру, ровно 2 изюмины). То есть получается, что p=2/10000 = 0,0002). В этом случае npq<10. В итоге, можем применять приближ формулу Пуассона.

 

СВ? Дискретная величина? Что назыв функцией распределения СВ? пример функции распределения некоторой дискретной сл вел, график.

Величина, принимающая в рез-тате испытания опред значение, называется СВ. СВ Х называется дискретной, если мн-во ее возможных значений конечно или счетно: Х(Ω)={x₁, x₂,…}. Функция, определенная в каждой точке х числовой оси формулой F_x(x)=F(x)=P(X<x)- функция распределения СВ Х. Пример:ряд распределения с.в. Х: F(x)^ 0 при х ≤1; 0.4 при 1<х≤4; 0.5 при 4<х≤5; 0.8 при 5<х≤7; 1.0 при х>7

Хi
Pi	0,4	0,1	0,3	0,2

 

 

Св-ва функции распределения СВ,пример.

ПримерР (Х=6)=F96+0)-F(6)=P(X<6+0)-P(X<6)=1-5/6=1/6

Может ли график функции распределения быть прямой линией?

Нет, не может, т.к.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: