Мат ожидание в случае распределения с плотностью f(x)? Может ли для какой-либо абсолютно непрерывн СВ не существовать мат ожидания?

Мат ожидание абсолютно непрерывн СВ Х с функцией плотности f(x) определяется рав-вом: М(Х)= интеграл xf(x)dx от минус беск до плюс беск Мат. ожидание СВ Е- число 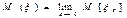. Если указанный справа предел не сущ-ет, то мат. ожидание величины х также считается несуществующим. Если ДСВ Х принимает счетное мн-во возможн знач, то , причем мат. ожидание существует, если ряд в правой части рав-ва сходится абсолютно. Т.к. ряд может и расходиться, то соотв. СВ может и не иметь мат. ожидания. На практике мн-во возможн знач СВ распространяется лишь на огранич участок оси абсцисс и, значит, мат. ожидание существует.

81. дисперсия в случае распределения с плотностью f (x)? Докажите, что для СВ X с плотностью 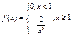дисперсия D (X) не существует, а мат ожидание M (X) существует.

Дисперсия абсолют непрерыв СВ. Дисперсия абсолютн непрерывн СВ X с функцией плотности f(x) и мат ожиданием m = M(X) определяется таким же равенством, как и для дискретной величины 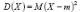Из рав-ва →, что справедлива след формула 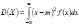. Поскольку формула может быть записана в след виде 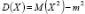то формулу можно представить таким образом 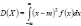. В случае когда абсолютн непрерыв СВ X сосредоточена на промежутке [a, b], формулы примут вид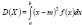 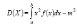. Дисперсия непрерывн СВ определяет степень рассеивания значений, принимаемых СВ, вокруг ее мат ожидания. Среднее квадратич отклонение, или стандарт отклонение, непрерывн СВ X определяется так же, как и для дискретной СВ: . Свойства мат ожидания и дисперсии.Для мат ожидания и дисперсии непрерывной СВ X сохраняются св-ва числовых характеристикДСВ. Постоян множитель выносится из под знака дисперсии в квадрате. 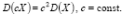Если к СВ прибавить конст, то дисперсия не изменится. 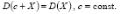Дисперсия суммы независ СВ равна сумме дисперсий этих величин.

82. формула для нахождения мат. ожидания и дисперсии СВ, равномерно распределенной на отрезке [a; b].

C.В. Х, сосредоточенная на [a;b], равномерно распределена на этом отрезке, если её функция плотности равна константе: f(х)=с (const), a≤х≤b. Значение постоян с определяется из условия: ∫^∞_-∞ f(х)dх=1, которому удовлетворяет любая плотность Р. В данном случае это условие принимает вид: с(b-a)=1→ что с=1/(b-a).

М(Х)= ∫^b_a хf(х)dх= ∫^b_a сdх, т.к. для абсолют непрерывн С.В. Х с непрерывн Р f(х) М(Х)= ∫^b_a хf(х)dх. Т.к. с=1/(b-a), то М(Х)=с*х²/2 |^b_a = c*(b²-a²)/2=(b+a)/2. получили, что числу М(Х) соответств середина [a; b]. Для нахождения дисперсии воспользуемся формулой, где D(Х)= ∫^b_a х²f(х)dх- m², где m=M(Х). D(Х)= 1/(b-a) ∫^b_a х²dх – ((a+b)/2)²= 1/(b-a)*(b³-a³)/3 - ((a+b)/2)²= (b²+ab+a²)/3 - ((a+b)/2)²= (b-a)²/12. Таким образом, М(Х)=(b+a)/2, а D(Х)= (b-a)²/12.

83.вероятностный смысл параметра m в формуле 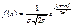для функции плотности СВ Х, распределенной по норм закону.

Формула 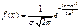описывает плотность норм распределения Р непрерывн с.в. Норм распределение определяется двумя параметрами: m и 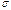. Достаточно знать эти параметры, чтобы задать норм распределение. Докажем, что вероятностный смысл этих параметров таков: m есть мат ожидание.

Поопределению мат ожидания непрерывн с.в., 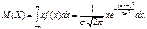Введем новую переменную 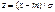. Отсюда . Приняв во внимание, что новые пределы интегрирования = старым, получим 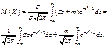. Первое из слагаемых = 0 (под знаком интеграла нечет функция; пределы интегрирования симметр относит начала координат). Второе из слагаемых равно m (интеграл Пуассона 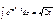). Итак, M(X)=m, т.е. мат ожидание норм распределения равно параметру m.

84. вероятностный смысл параметра σ в формуле для функции плотности 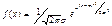СВ, распределенной по норм закону.

Докажем, что 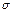- среднее квадратич отклонение норм распределения. Введем новую переменную z==(х—m)/ 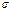. Отсюда 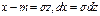. Приняв во внимание, что новые пределы инте­грирования = старым, получим Интегрируя по частям, положив u=z, найдем → 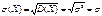.Итак, среднее квадратич отклонение норм распределения = .

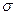85. Докажите, что для СВ, распределенной по показат закону с параметром 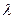, мат ожидание

Найти числовые характеристики СВ X, распределенной по показат закону с плотностью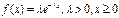

Для нахождения мат ожидания воспользуемся формулой M(X)= 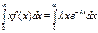. Найдем интеграл методом интегрирования по частям, полагая u = x, dv = e ^{–λ x} d (λ x), так что du = dx, v = – e ^{–λ x} . Получим 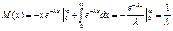. Таким образом, M(X)=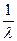

86 СВ X равномерно распределена на отрезке [a,b]. Можно ли для любых m и δ>0 подобрать параметры a и b так, чтобы M(x)=m, D(x)=δ²? Как по m и δ найти a и b?

СВ Х, сосред. на [a,b] называется равном. распередёлнной, если её на [a,b].

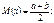
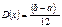докажем это

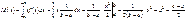
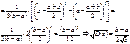
Если M(x)=m, а D(x)= δ² и m, δ>0 – любые, тогда мы всегда можем подобрать a и b, чтобы выполнялось это усл.

Пример: пусть m=3, δ=4 – тогда ;

; ; ;

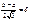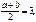
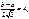
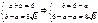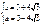
87.Что такое правило 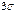для норм распр? Верно ли, что для любой норм СВ Х сущ отрезок 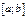, для кот 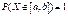? Ответ обоснуйте.

Правило трех сигм – отклонение любой СВ от ее мат ожидания будет <= 3-х средних кв откл (по abs величине). Правило трех сигм применимо для большинства СВ, встречающихся на практике. P (|X-a|<=3сигма) для норм закона = 0,9973. Для равномерного закона =1. Для показательного = 0,9827 и т.д.

Для норм распр. СВ Х справедлива формула Преобразуем эту формулу, приняв 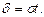получим 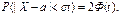Если t=3 → 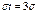, то 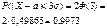, т.е. вер того, что откл по abs величине будет < утроенного ср кв. откл. равна 0,9973. Верно