Дискретная СВ? Может ли табл рассматриваться как закон распределения дискретнойСВ?

Х	-10
Р	0,2	0,4	0,3

СВ Х-дискретная, если мн-во ее значений не более чем счетно, т.е конечно или счетно. По определению сумма значений строчке Р должна быть равна 1. То есть, нет не может.

Дана дискретная СВ с законом распределения

Х	X1	X2	…	Xn
Р	P1	P2	…	pn

Что является её функцией распределения F(x)? Постройте график F(x) и опишите его точки разрыва. Как вычисляется ? Пусть х о - любое число. Среди чисел х₁, x₂,... выделим те, ко­торые меньше х₀. Пусть ими будут х_i1, x_i2,.... Событие x<х0 явля­ется суммой событий X = х_i2, X – x_i1,..., поэтому его Р= p_i1 + p_i2 +...; F(x)= ∑p_i График для X на три значения: х_ь х₂, х_з. x₁ < х₂ < х_з. График представляет собой ступенчатую лома­ную со скачками в точках х₁ х₂, х₃. Величины скачков равны соответств p₁,p₂,p₃ - Левее график совпадает с осью Ох, правее c прямой y=1. P(a≤X≤b)=P(b)-P(a).

Геометрич распределение с параметром p?пример опытов, в котором определена СВ, распределенная по геометрич закону с параметром p?

ДСВ Х имеет геометрич распределение, если она принимает значения 1, 2, 3, ….с р(Х = k) = q ^(k-1)p (т.е. Р образуют убывающую геометрич прогрессию с первым членом р и знаменателем q). Производит­ся ряд независ опытов, в каждом из которых с одной и той же Р наступает соб А. Опыты продолжаются до пер­вого появления соб А, после чего прекращаются. Рассматрива­ется СВ- х число произведенных опытов.
Событие Х= n (n - любое натуральное) означает, что в первых п- 1
опытах событие А не наступает, а в n-м опыте наступает. Р такого исхода равна: pq^n-1 где q = 1 -р. Следовательно, закон распределения величины X будет:

 

X		2			п
р	р	pq	pq2		pqn-1

Что называется бином распределением с параметрами n и p?пример опытов, в котором определенаСВ, распределенная по бином закону.

Распределение Р, определяемое формулой Бернулли, называется бином законом распределения СВ. Пусть произ­водится определенное число п независ опытов. В каждом из них с одной и той же р может наступить некоторое соб А. Рассматриваемая СВ(Х)- число наступ­лений соб А в п опытах. Соответств табл имеет вид: где P_n(k)=C_n^kp^k(1-p)^n-k

X			л-1	п
р	Pn(0)	pn(1)	Pn(n-1)	Pn(n)

 

 

48. Какой закон распределения называется законом Пуассона? Увяжите с предельной теоремой Пуассона.

Если число испытаний велико, а p появления соб в каждом испытании очень мала,то используют формулу , где - число появлений соб в n независ испытаниях, l= np (среднее число появлений соб в n испытаниях), и говорят, что с.в.распределена по закону Пуассона.

X			K	…
p				…

 

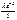
49. Как определяется независ СВ? кость бросают 200 раз. Пусть X₁ – число выпадений грани 1; X₂ – число выпадений грани 2. Будут ли завис СВм X₁ и X₂?

 

X и Y независимы, если выполняется равенство P(X=a, Y=b) = P(X=a)P(Y=b). P(X₁=200) = (1/6)²⁰⁰ (т.к. опыт проводился 200 раз). Следовательно, можно записать P(X₁=200, Y₁=200) = 0. Однако такого быть не может, т.к. если одна грань выпала 200 раз, то вторая уже не может (она эти 200 раз не выпала). Следовательно эти величины зависимы.

 

50. Пусть X,Y,X – независ СВ, принимающие с вероятностью 1\2 значения 0 и 1. Верно ли, что X+Y и Y+Z – независ СВ?

Y+z
p	1\4	1\2	1\4

 

X,y,z
p	1\2	1\2

 

X+y
p	1\4	1\2	1\4

P(x+y=0, y+z=0)=P(x=y+z=0)=1\8; P(x=0)*P(y=0)*P(z=0); P(x+y=0)*P(y+z=0)=1\16 – P(x+y,y+z)=1\4*1\4

1\8¹1\16 - зависимые.

 

 

51. мат ожидания ДСВ. Поясните его смысл на примере СВ с двумя возможными значениями, исходя из статистич определения Р. Пусть СВ X связана с некоторым опытом. Провели n испытаний и при этом возникла статистика

Xi	X1	X2
ni	n1	n2

Найдем среднее значение X = _è при n стремящимся к бесконечности = X₁*p₁ + X₂*p₂ т.к по статистич определению Р соб примерно равна отношению числа успехов к общему числу испытаний. Lim X = X₁*p₁ + X₂*p₂ M(X))

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: