 |
Временная диаграмма мгновенной мощности
|
|
|
|
p (θ) = u (θ) · i (θ) = 2 UI ·sin q · sin (q – j) = UI [cos j – cos(2 θ – j)]
также приведена на рис. 1.4,а. Кривая мгновенной мощности является знакопеременной: на интервалах от j до p и от (p + j) до 2 p мгновенная мощность положительна, и энергия передается от источника в нагрузку; напротив, на интервалах от 0 до j и от p до (p + j) мгновенная мощность отрицательна, и энергия возвращается из нагрузки в источник питания. Активная мощность равна среднему значению мгновенной мощности за период повторения:
P = 
 = UI cos j.
= UI cos j.
Величина P также показана на диаграммах рис. 1.4,а.
Полная мощность S = UI, а коэффициент мощности
c =  = cos j,
= cos j,
его значение меньше 1. При нулевом фазовом угле (работа на активную нагрузку) χ = 1. При фазовом угле, равном 90 град, активная мощность и коэффициент мощности равен нулю (работа на индуктивную нагрузку). Что же характеризует коэффициент мощности?
Рассмотрим энергообмен между сетью и нагрузкой более подробно. Разложим ток i на две составляющие: активную, синфазную напряжению, и реактивную, отстающую от напряжения на угол 90 град:
i = i а + i р =  I · cos j · sin q +
I · cos j · sin q +  I ·sin j · sin(q – p/2).
I ·sin j · sin(q – p/2).
Кривые составляющих тока приведены на рис. 1.4,б и 1.4,в. Кривую мгновенной мощности также разложим на две составляющие: активную составляющую мгновенной мощности, обусловленную активной составляющей тока, и реактивную, обусловленную реактивной составляющей тока:
р = p а + p р = UI ·cos j ·sin2 q + UI · sin j ·sin (q – p /2)·sin q.
Кривые мгновенной активной и реактивной мощностей представлены на рис. 1.4,б и 1.4,в. Кривая активной мгновенной мощности по форме совпадает с кривой мгновенной мощности при работе сети на активную нагрузку. Среднее значение p а равно активной мощности

Напротив, кривая реактивной мгновенной мощности не имеет постоянной составляющей. Следовательно, активная мощность переносится из источника в нагрузку активной составляющей тока, а реактивная составляющая тока выявляет бесполезные колебания энергии между источником и нагрузкой. Обобщенной характеристикой этого энергообмена является реактивная мощность сдвига Q, которую можно представить себе как вектор, ортогональный вектору P. Существует договоренность, считать реактивную мощность при отстающем от напряжения токе положительной величиной.
|
|
|
Таким образом, активная мощность и реактивная мощность сдвига являются составляющими полной мощности:
S 2 = P 2 + Q 2.
Отсюда
Q 2 = S 2 – P 2 = S 2 (1 – cos2 j);
Q = S sin j.
Аналогичный анализ можно провести и для параллельной RL- нагрузки, для RC -нагрузки и для любой разветвленной линейной цепи. Отличие емкостной нагрузки заключается в том, что ток i имеет опережающий характер относительно сетевого напряжения, и реактивная мощность Q – отрицательная. В любом случае источник синусоидального напряжения, работающий на линейную нагрузку, содержащую активные и реактивные элементы, формирует ток i синусоидальной формы, имеющий по отношению к напряжению отстающий или опережающий фазовый сдвиг j.
1.3.Источники и компенсаторы реактивной мощности
Большинство потребителей электроэнергии, подключенных к электрическим сетям переменного тока, имеют индуктивную реакцию и коэффициент мощности χ, существенно меньший 1. При передаче энергии от электростанции через линии электропередач (ЛЭП) к потребителю осуществляется многократная трансформация электроэнергии, которая сопровождается не только потерями энергии, но и снижением коэффициента мощности, что обусловлено индуктивными сопротивлениями трансформаторов. ЛЭП (кроме наиболее высоковольтных) сами имеют индуктивное сопротивление. Все это указывает на значительное потребление реактивной мощности. При этом возникает серьезная техническая проблема, связанная со следующими факторами:
|
|
|
1. В энергосистеме необходимо поддерживать баланс не только активных, но и реактивных мощностей. При нехватке в энергосистеме реактивной мощности происходит снижение частоты сети, что жестко ограничено ГОСТом (см. § 3.5).
2. Реактивная мощность не связана с выполнением работы. Для передачи потребителю той же активной мощности при снижении коэффициента мощности необходимо увеличение токов, это требует увеличение затрат на проводниковые изделия, трансформаторы, коммутационные устройства.
3. В сетях ограниченной мощности, которые нельзя представить в виде источника э.д.с. (см. гл. 3), увеличение потерь при передаче электроэнергии приводит к снижению напряжения на зажимах потребителя.
Поэтому повышение коэффициента мощности за счет снижения доли реактивной мощности является важной экономической задачей. Работа на нагрузку с низким коэффициентом мощности приводит к экономическим издержкам. Для решения поставленной задачи необходимо создавать источники реактивной мощности, однако это требует значительных затрат.
Полярность величины Q является условной, поэтому источники реактивной мощности называют часто компенсаторами реактивной мощности (КРМ). КРМ следует устанавливать непосредственно вблизи мощных энергопотребителей с тем, чтобы не загружать сети передачей реактивных токов. Система «потребитель энергии - КРМ» должна иметь бóльший коэффициент мощности, чем потребитель без компенсатора.
Существуют следующие типы КРМ: синхронные компенсаторы, емкостные КРМ, активные КРМ реактивной мощности сдвига.
1. Синхронные компенсаторы. Это синхронные электрические машины, работающие с перевозбуждением без нагрузки на валу. При этом ток на зажимах генератора опережает напряжение, т.е. генерируется реактивная мощность сдвига емкостного характера (Q < 0). При работе синхронного компенсатора в нем происходят некоторые потери энергии.
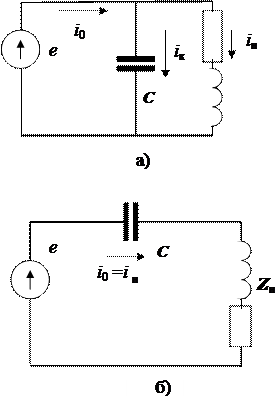
2. Емкостные КРМ (косинусные конденсаторы) в настоящее время являются основным типом КРМ. КРМ делятся на параллельные (конденсатор С подключается параллельно энергопотребителю) и последовательные (конденсатор С подключается последовательно потребителю) Схемы приведены на рис. 1.5.
|
|
|
 |
Z н
Рис. 1.5
Рассмотрим параллельный КРМ рис.1.5,а. Потребитель энергии представляем последовательной схемой замещения Z н = R + jXL = Z нcos φ + + jZ нsin φ, а его проводимость
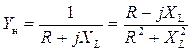 .
.
Сопротивление КРМ – jXC, а проводимость YC = j / XC.
Входная проводимость системы «КРМ – потребитель энергии» равна

Фазовый угол системы
j с = arctan[ Im(Y)/Re(Y)].
Коэффициент мощности c = cos jс.
Полная компенсация реактивной мощности потребителя достигается, если входное сопротивление системы имеет активный характер, при этом мнимая часть проводимости Y равна нулю, т.е.
 = 0.
= 0.
|
|
|


