Ток в нагрузке несинусоидален

i (t)= U_m sin(wt) · y (t) = U_m sin(wt) · Y ₀ sin(w_рt) =

= U_mY ₀ {sin(wt) – 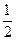cos[(w + w _р) t ] + 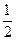cos[(w - w _р) t ]}.

Кривая мгновенной мощности (рис. 2.1,б) однополярна:

p (t) = U_m ² Y₀ sin(wt) {sin(wt) – 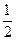cos[(w + w _р) t ] + 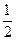cos[(w - w _р) t ]}.

 

 

 

Рис. 2.1

 

Активная мощность вычисляется на всем периоде частоты повторения

P = ,

она определяется только первой гармонической составляющей тока с частотой сети, поскольку произведение колебаний двух разных частот не дает постоянной составляющей

P = U ² Y ₀.

Действующее значение тока равно корню из суммы квадратов каждой гармоники тока:

I = U ·Y₀ =1,22 U ·Y₀.

Полная мощность

S = UI = 1,22 U ² Y ₀.

Коэффициент мощности

c = P / S = 0,82.

Таким образом, появляется еще одна составляющая полной мощности, вызванная несинусоидальностью тока, мощность искажения T. В нашем примере реактивная мощность сдвига отсутствует (Q = 0) и

S² = P² + T²;

На основании рассмотрения примера можно сделать обобщающие выводы:

1.Нестационарные процессы в линейных цепях приводят появлению несинусоидальных токов, которые содержат дополнительные гармоники, частота которых не кратна частоте сети (неканонические гармоники).

2.При этом появляется мощность искажения T и коэффициент мощности снижается.

Таким образом, мы вторглись в область несинусоидальных сигналов. В нелинейных цепях кривые токов несинусоидальны и в установившихся режимах, поэтому в них всегда присутствует мощность искажения. Рассмотрение ее природы нам предстоит в следующем разделе.

 

 

2.2. Коэффициент мощности неуправляемых выпрямителей

 

В цепях с нелинейной нагрузкой несинусоидальность токов проявляется и в установившемся режиме. Вопросы Теории мощности для нелинейных цепей целесообразно рассмотреть, выбрав нелинейные цепи, которые распространены в полупроводниковой преобразовательной технике. В силовой электронике среди нелинейных элементов преобладающее распространение имеют полупроводниковые ключевые элементы, которые характеризуются двумя состояниями - открытым (падение напряжения на идеальном ключе равно нулю), и запертым (ток, протекающий через идеальный ключ равен нулю). Ключевым элементом является диод, проводящий ток при положительном напряжении между анодом и катодом, и запертый для тока при приложении напряжения обратной полярности. Полупроводниковые диоды достаточно близки по своим свойствам к идеальным ключам - падение напряжения на диоде в открытом состоянии очень мало, обратный ток при приложении обратного напряжения также очень мал.

Рассмотрим простейшую схему выпрямления - двухполупериодный мостовой вы прямитель (рис. 2.2) с различными видами нагрузок. Будем считать диоды идеальными ключами.

1. Активная нагрузка Z _н= = R. При положительной полуволне напряжения сети e > 0 открыты диоды V 1 (на аноде положительное напряжение) и V 2 (на катоде отрицательное напряжение). Напряжение на нагрузке u_d = e, ток сети i ₀ протекает через V 1, нагрузку и V 2, i_d = i ₀.

При отрицательной полуволне напряжения сети e < 0 открыты диоды V3 (на аноде положительное напряжение) и V 4 (на катоде отрицательное напряжение). Напряжение на

нагрузке u_d = – e, ток сети i ₀ протекает через V 3, нагрузку и V 4 в том же направлении, что и на первом полупериоде, i_d = – i ₀.

Временные диаграммы токов и напряжений на входе и выходе устройства приведены на рис. 2.3,а, б.

При напряжении сети напряжение на нагрузке

,

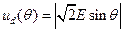ток нагрузки

,

а ток сети

 

Ток i ₀ синусоидален и синфазен напряжению сети, следовательно, коэффициент мощности χ = 1. Полная мощность на входе и выходе выпрямителя S = E ² / R равна активной мощности P. С точки зрения влияния преобразователя на питающую сеть такой режим является оптимальным. Но для потребителя электрической энергии постоянного тока этот режим неблагоприятен.

Рис. 2.3

 

 

Полезной составляющей при выпрямлении является постоянная составляющая (или среднее значение) выходного напряжения u_d, которую обозначают U_d и определяют

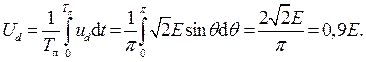(2.1)

В этой формуле мы учли, что период повторения кривой выходного напряжения выпрямителя в угловых координатах равен π. Величина U_d показана на рис. 2.3,б.

Активная мощность, которая передается на постоянной составляющей в нагрузку, равна

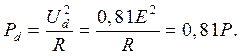
Это означает, что 19% активной мощности передается в нагрузку переменной составляющей тока, поэтому такое выпрямление следует считать некачественным.

2. Активно-индуктивная нагрузка. Энергетические процессы в схеме рис. 2.2 значительно изменяются при работе на активно-индуктивную нагрузку Z = R + jωL. Индуктивным сопротивлением обладают многие потребители энергии постоянного тока, в ряде случаев нагрузка подключается к выходу выпрямителя через индуктивный фильтр.

Временные диаграммы напряжений и токов на входе и выходе выпрямителя представлены на рис. 2.4,а и б. Интервал проводимости диодов и форма напряжений при подключении в цепи постоянного тока дросселя не изменяются (сравни рис. 2.3). Величина постоянной составляющей выходного напряжения по-прежнему определяется выражением (2.1).

Значительно изменяется форма тока нагрузки i_d (θ). Напряжение u_d (θ) прикладывается к RL -цепи, которая для постоянной составляющей обладает сопротивлением R, а для высших гармоник индуктивное сопротивление ωL значительно, поэтому пульсации выходного тока выпрямителя уменьшаются. При достаточно большой индуктивности можно пренебречь пульсациями, и считать ток нагрузки постоянным i_d = I_d = U_d /R. При анализе в дальнейшем для упрощения математического аппарата рассматриваем именно этот достаточно характерный для выпрямителей режим работы.

Ток i ₀, потребляемый выпрямителем от сети, имеет при этом несинусоидальную (прямоугольную) форму. В выпрямителе без потерь мгновенные мощности на входе и на выходе равны: p (θ) = e (θ)· i ₀(θ) = u_d (θ)· i_d (θ). Кривая мгновенной мощности однополярна и повторяет форму напряжения u_d (см. рис. 2.4,б).

Найдем коэффициент мощности выпрямителя. Ток сети имеет амплитуду I _0m = I_d = U_d/R. Действующее значение сетевого тока

 

Полная мощность S = E · I₀ = E · I_d.

Активная мощность переносится в нагрузку только на постоянном токе, т.к. пульсации тока на выходе отсутствуют. Поэтому P = P_d = U_d ·I_d = E·I_d.

Коэффициент мощности

 

Снижение коэффициента мощности вызвано несинуcоидальностью сетевого тока. Однако кривая мгновенной мощности p (θ) однополярна и не фиксирует энергообмена между сетью и выпрямителем. Для того, чтобы разобраться в процессе энергообмена, разложим ток i ₀ в ряд Фурье (в силу симметрии полуволн в нем содержатся только нечетные гармоники) на периоде повторения T _п

В данном режиме все гармоники содержат только синусные составляющие, поэтому находим только коэффициент

Рис. 2.4

 

 

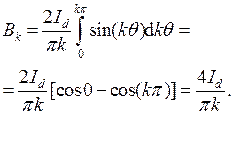
Следовательно, разложение в ряд Фурье сетевого тока

На рис. 2.4,в представлена первая гармоника сетевого тока i ₀₁, синфазная напряжению сети, а на рис. 2.4, г сумма высших гармоник (высшие гармоники, частота которых кратна частоте сети называются каноническими) i _0в = = i ₀₃ + i ₀₅ + i ₀₇ +…

Мгновенная мощность p также может быть представлена в виде суммы мгновенной мощности от первой гармоники p ₁, представленной на рис. 2.4,в, и мгновенной мощности от высших гармоник p _в, показанной на рис. 2.4,г: p = p ₁ + p _в = e · i ₀₁ + e · i _0в. Кривая мгновенной мощности p ₁ однополярна, и активная мощность, переносимая первой гармоникой, равна активной мощности, передаваемой в нагрузку:

Кривая p _в знакопеременна и не имеет постоянной составляющей, высшие гармоники сетевого тока не участвуют в передаче активной мощности.

Итак, активная мощность передается только первой гармоникой сетевого тока. Высшие гармоники тока вызывают только бесполезный обмен энергией между сетью и входной цепью выпрямителя. Этот энергообмен и характеризуется мощностью искажения T.

Действующее значение первой гармоники сетевого тока I ₀₁ = = B ₁/ = . Отношение I ₀₁ к действующему значению сетевого тока I ₀ называется коэффициентом искажения

.

При кривая сетевого тока синусоидальна. В рассмотренном режиме

Полная мощность S в неуправляемом выпрямителе состоит из активной мощности P и мощности искажения T. Поскольку мощность искажения не связана с выполнением работы, то ее вектор считают ортогональным активной мощности, таким образом

T ²= Q ² – P ² = S ² – n ² S ² = (1 – n ²) S ².

 

3. Выпрямитель с емкостным фильтром. Широко применяемая схема однофазного мостового выпрямителя с емкостным фильтром приведена на рис. 2.5,а. При достаточно большой емкости конденсатора С пульсации напряжения на нагрузке u_d отсутствуют и можно полагать напряжение на нагрузке постоянным u_d = u_C = U_d.

 

 

 

 

Рис. 2.5

 

При включении пары диодов V 1 – V 2 (или V 3 – V 4) ток i ₀, заряжающий конденсатор С, ограничен только потерями в диодах схемы, эти потери отражены введением в схему резистора r _п, показанного пунктиром. Ток сети i ₀ протекает только в те моменты времени, когда абсолютная величина напряжения сети e превышает напряжение на конденсаторе u_d. Угловая длительность интервала проводимости на полупериоде сети равна 2 Θ. Форма тока сети приведена на рис. 2.5,б, он имеет несинусоидальный импульсный характер. Проведено разложение тока i ₀₁ в ряд Фурье, определено действующее значение тока и его первой гармоники, вычислен коэффициент искажения сетевого тока ν = χ. На рис. 2.5,в приведены зависимости относительного выходного напряжения выпрямителя U_d / E и коэффициента искажения ν от параметра Θ.

Зависимости свидетельствуют о низком коэффициенте мощности выпрямителей с емкостным фильтром. Их широкое распространение объясняется низкой стоимостью и благоприятными массогабаритными показателями. По мере внедрения стандартов, лимитирующих искажения сетевого тока выпрямителей, применение выпрямителей с емкостным фильтром будет ограничено устройствами мощностью до 50 Вт.

4. В заключение обзора неуправляемых выпрямителей остановимся кратко на особенностях трехфазных выпрямителей, которые преимущественно применяются в области средних и больших мощностей (начиная с нескольких кВт). Наиболее распространенной схемой трехфазного выпрямителя является мостовая схема, приведенная на рис. 2.6,а. Устройство выполнено на шести диодах, которых объединены в две группы: катодную группу, объединенную катодами, V 1, V 3 и V 5, и анодную группу, диоды V 2, V 4 и V 6, объединенные анодами.

В катодной группе ток проводит только один диод, напряжение на аноде которого наиболее положительно. Интервал проводимости равен 120^о. В анодной группе также проводит только один диод, напряжение на катоде у которого наиболее отрицательно. Ток нагрузки i_d протекает через два последовательно включенных диода, например, через V 1 и V 2. Ток нагрузки сглажен индуктивностью и поэтому имеет малые пульсации, поэтому токи через диоды имеют форму прямоугольных импульсов. Фазные сетевые токи, потребляемые из сети, i_{A 0}, i_{B 0} и i_{C 0}, являются суммой токов двух диодов, подключенных к фазе сети, форма тока i_{A 0} показана на рис. 2.6,б.

 

а) б)

Рис. 2.6

Действующее значение каждого из фазных токов сети равно I ₀ = Разложим ток в ряд Фурье. В фазном токе содержатся только нечетные гармоники за исключением гармоник, кратных трем. Найдем первую гармонику. Она синфазна фазному напряжению сети, и ее действующее значение составляет 0,955 I ₀. Следовательно, коэффициент мощности трехфазного мостового неуправляемого выпрямителя χ = ν = 0,955, что выше коэффициента мощности однофазного неуправляемого выпрямителя. Повышение коэффициента мощности связано с увеличением коэффициента искажений ν за счет исключения в сетевом токе гармоник, кратных трем. Повышенный коэффициент мощности является важным преимуществом трехфазных выпрямителей по сравнению с однофазными.

Таким образом, вентильный преобразователь, являясь нелинейным устройством, способен потреблять из сети несинусоидальный ток, в результате этого сеть загружается высшими гармоническими составляющими тока, которые не передают активной мощности. Рассмотренные выше неуправляемые выпрямители не способны регулировать или стабилизировать величину выходного напряжения. Продолжим рассмотрение, обратившись к выпрямителям, которые обладают этой способностью.

 

2.3. Коэффициент мощности управляемых выпрямителей

 

Мостовая схема управляемого однофазного выпрямителя приведена на рис. 2.7. Она повторяет схему неуправляемого выпрямителя рис. 2.2, но неуправляемые полупроводниковые приборы (диоды) заменены на управляемые ключи. В качестве ключей могут использоваться различные полупроводниковые ключевые управляемые приборы. При анализе полагаем ключи идеальными. Для исключения выделения мощности в нагрузке на переменной составляющей применяется RL -нагрузка. С целью упрощения анализа полагаем индуктивность нагрузки L большой, переменными составляющими тока нагрузки i_d пренебрегаем.

При выборе алгоритмов переключения необходимо обеспечить два условия:

1. Ток нагрузки индуктивного характера нельзя прерывать при размыкании ключей, поэтому всегда должен быть открыт один из ключей пары (V 1 – V 3) либо пары (V 2 – V 4).

2. Недопустимо закорачивание сети при одновременном включении V 1 и V 3 (либо V 2 и V 4).

Таким образом, ключи V 1 и V 3 (либо ключи V 2 и V 4) переключаются комплиментарно, т.е. вместо закрывшегося мгновенно включается второй ключ пары.

Исходя из этих ограничений, возможны четыре состояния схемы:

Вариант В1 – замкнуты ключи V 1 и V 2, ток источника i ₀ протекает через V 1, нагрузку, V 2 и возвращается в источник: i ₀ = i_d, u_d = e.

Вариант В2 – замкнуты ключи V 3 и V 4, ток источника протекает через V 3, нагрузку, V 4 и возвращается в источник: i ₀ = – i_d, u_d = – e.

Вариант В3 – нагрузка закорочена ключами V 1 и V 4, ток источника отсутствует: i ₀ = 0. Поскольку на идеальных замкнутых ключах нет потерь напряжения, то u_d = 0.

Вариант В4 - нагрузка закорочена ключами V 2 и V 3, ток источника отсутствует: i ₀ = 0, u_d = 0.

Мгновенная мощность нагрузки всегда равна мгновенной мощности на входе преобразователя.

Рассмотрим два варианта управления работой ключей.

1. Фазовое регулирование мощности нагрузки. Для регулирования мощности и напряжения на нагрузке необходимо управлять моментами отпирания и запирания ключей с помощью системы управления (на рис. 2.7 не показана). Наибольшее распространение получило фазовое управление, при котором моменты замыкания ключей задерживаются относительно момента перехода напряжения сети через ноль на угол задержки включения a. Варианты В 3 и В 4 при этом не используются, поэтому речь идет о задержке на угол α не только моментов замыканий, но и размыканий ключей. Форма напряжений и токов на входе и выходе выпрямителя представлена на рис. 2.8,а и б. На интервале α ÷ π+α проводят ток ключи V 1 и V 2 (вариант В 1), на остальной части периода – ключи V 3 и V 4 (вариант В 2). Периодом повторения кривой u_d является половина периода напряжения сети, поэтому среднее значение выходного напряжения может быть найдено путем усреднения на половине периода:

U_d = (2.2)

При a < p/ 2 среднее напряжение на нагрузке положительно. Мы ограничим рассмотрение только этим режимом, называемым выпрямительным. Нетрудно видеть, что рассматриваемый нами алгоритм управления при a = 0 сводится к рассмотренному в § 2.2 неуправляемому режиму.

Ток нагрузки I_d(t) = I_d =U_d / R. Ток i ₀ имеет прямоугольную форму, однако в отличие от неуправляемого выпрямителя этот ток сдвинут относительно напряжения e на угол a (см. рис. 2.8,а).

Кривые мгновенной мощности на входе и выходе преобразователя совпадают, они повторяют форму u_d. Эти кривые приведены на рис. 2.8,б:

Периодом повторения этой функции является половина периода, поэтому активная мощность, выделяемая в нагрузке, может быть найдена путем усреднения на половине периода

P =

Она же равна активной мощности на входе преобразователя. Мощность, выделяемая на постоянной составляющей P_d = U_d·I_d = P. Таким образом, выделение мощности на переменной составляющей в нагрузке отсутствует.

Действующее значение входного тока, имеющего прямоугольную форму, I ₀ = I_d.

 

Полная мощность S = E · I ₀. Коэффициент мощности

За счет сдвига тока i ₀ на угол a появился сомножитель cos a. Форма тока по сравнению с неуправляемым выпрямтителем (см. § 2.2) не изменилась, и по-прежнему коэффициент искажения тока

n = I ₀₁/ I ₀ = 0,9.

Поэтому коэффициент мощности мощно записать в виде

c = n· cos a.

Мы видим, что с увеличением угла задержки включения α коэффициент мощности уменьшается. Исследуем это явление более подробно, для этого разделим ток i ₀ на две составляющие - первую гармонику и сумму высших гармоник:

i ₀(θ) = i ₀₁ (θ)+ i _0в (θ).

Указанные составляющие приведены на рис. 2.8,в и г. Аналогично разделим на две составляющие мгновенную мощности:

p (θ) = p ₁(θ) + p _в(θ),

где р ₁(θ) = e (θ)· i ₀₁(θ),

р _в(θ) = e (θ) · i _0в (θ).

Рис. 2.7

Кривые мгновенных мощностей р ₁ и p _в показаны на рис. 2.8,в и г. Кривая р ₁ такая же как при работе синусодальной сети на линейную комплексную нагрузку (см. рис. 1.4,а). Легко убедиться, что фазовый сдвиг первой гармоники тока относительно напряжения e j = a. Среднее значение p ₁ по аналогии с § 1.2

Рис. 2.8

P ₁ = E · I ₀₁сos a = E·I ₀· n cos a = P.

P=S·n cos a.

 

Процессы энергообмена между преобразователем и сетью на первой гармонике протекают так же, как и при работе источника на линейную нагрузку. За счет фазового сдвига тока происходит периодический энергообмен между источником и преобразователем. Если разделить первую гармонику тока на активную и реактивную составляющие, то мы увидим, что активная, синфазная напряжению, составляющая первой гармоники тока переносит активную мощность, а реактивная, отстающая от напряжения на 90^о, составляющая свидетельствует о потреблении преобразователем реактивной мощности сдвига

Q = S · n · sin j.

Кривая мгновенной мощности p _в не имеет постоянной составляющей, поскольку при перемножении колебаний разных частот разностная частота никогда не дает постоянную составляющую. Следовательно, как уже отмечено в § 2.2, высшие гармоники тока не переносят активной мощности и характеризуют лишь бесполезные колебания энергии между источником e и преобразователем, эти колебания характеризуются мощностью искажения T.

Итак, в рассматриваемом преобразователе полная мощность состоит из активной составляющей, реактивной мощности сдвига и мощности искажений, при этом

S ² = P ² + Q ² + T ².

Всё рассмотренное нами имеет всеобщий характер, и характеризует работу синусоидальной сети на любой нелинейный однофазный токоприемник. Все приведенные выше формулы, обладающие всеобщностью, выделены рамочками.

Сделаем практические выводы. Для уменьшения напряжения U_d на выходе выпрямителя осуществляется перераспределение составляющих полной мощности: активная мощность уменьшается, а доля реактивной мощности возрастает, поскольку увеличивается фазовый сдвиг тока, потребляемого преобразователем относительно напряжения. В результате значительно уменьшается коэффициент мощности.

На рис. 2.9,а показаны зависимости коэффициента мощности, cos j, коэффициента искажения тока и угла задержки включения a от активной мощности нагрузки, отнесенной к ее максимальному значению, а на рис. 2.9,б зависимости активной, реактивной, полной мощностей и мощности искажения от активной мощности нагрузки (R = const).

Последствия работы сети на нагрузку с низким коэффициентом мощности нам уже известны. Ниже мы обсудим негативное влияние мощности искажения. Низкий коэффициент мощности при глубоком регулировании мощности нагрузки является характерной чертой простейших преобразователей, и стремление к его повышению является одной из основных задач силовой электроники.

 

 

 

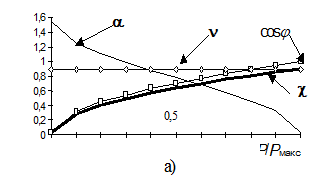
Рис. 2.9

 

2. Широтное регулирование мощности нагрузки. Фазовое управление связано с внесением фазового сдвига входного тока преобразователя относительно напряжения сети. Широтное управление позволяет его исключить. Рассмотрим формирование симметричной кривой выходного напряжения. Временные диаграммы напряжений и токов на входе и выходе выпрямителя приведены на рис. 2.10,а и б.

На интервале от 0 до a напряжение на нагрузке равно нулю, так как ключи включены по варианту В 3 (или В 4), на интервале от a до (p – a) используется вариант включения В 1 и напряжение на нагрузке равно e. На интервале (p – a) до (p + a) напряжение на нагрузке снова нулевое (варианты В 3 или В 4), а на интервале от (p + a) до (2p – a) реализуется вариант В 2 и напряжение на нагрузке равно – e, затем до момента 2 p напряжение на нагрузке снова равно нулю.

Среднее значение напряжения на нагрузке имеет то же значение, что и при фазовом управлении (см. выражение (2.2)):

Ток нагрузки равен

I_d(t) = I_d =U_d / R.

Рис. 2.10

 

Ток i ₀, потребляемый преобразователем от сети, имеет прямоугольную форму, в отличие тока при фазовом управлении он не имеет сдвига фазы относительно напряжения e, но содержит паузы. Относительная длительность протекания тока

g = 1 – 2 a/p.

Нетрудно видеть, что рассматриваемый нами алгоритм переключения при a = 0 сводится к рассмотренному в § 2.2 неуправляемому режиму.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: