Токи в системе также симметричны

i_A = I sin(q – j),

i_B = I sin(q – j – 2 p /3),

i_C = I sin(q – j – 4 p /3.

где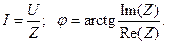

 

 

Рис. 1.8

 

Мгновенная мощность в каждой фазе определяется так же, как и в однофазных цепях (см. § 1.2)

p_A = u_A · i_A = 2 UI · sin q · sin(q – j) = UI [cos j – cos(2 q – j)];

p_B = u_A · i_B = 2 UI · sin q · sin(q – j) = UI [cos j – cos(2 q – 2 p /3 – j)];

p_C = u_C · i_C = 2 UI · sin q · sin(q – j) = UI [cos j – cos(2 q – 4 p /3 – j)].

Мгновенная мощность трехфазной сети равна сумме мгновенных мощностей фаз. В симметричной системе при суммировании переменная составляющая мгновенных мощностей взаимно уравновешивается и кривая мгновенной мощности не имеет пульсации:

p = p_A + p_B + p_C = 3 UI cos j.

Активная мощность трехфазной системы равна сумме активных мощностей фаз или среднему значению мгновенной мощности p на периоде повторения:

P = P_A + P_B +P_C = = 3 UI cos φ,

a реактивная мощность равна соответственно Q = Q_A + Q_B +Q_C = 3 UI sin φ.

Полная (кажущаяся) мощность трехфазной системы равна сумме произведений действующих значений напряжений на действующие значений токов в каждой фазе: S = S_A + S_B + S_C = U_A I_A + U_B I_B + U_C I_C = 3 UI.

Коэффициент мощности в симметричной трехфазной системе равен c = P / S = cos j.

 

 

1.5.Энергетические процессы в несимметричных

трехфазных цепях

 

Воспользуемся схемой рис. 1.8. Рассматриваем питание несимметричной трехфазной цепи нагрузки от симметричной системы трехфазных напряжений. Нагрузочные сопротивления фаз выразим через модули сопротивлений и фазовые углы каждой фазы:

Z_A = Z_A (cos j_A + j cos j_A),

Z_B = Z_B (cos j_B + j cos j_B),

Z_A = Z_C (cos j_C + j cos j_C).

При этом система токов будет также несимметричной, причем токи могут иметь как амплитудную несимметрию, так и фазовую несимметрию. При несимметрии нагрузки трех- и четырехпроводная системы проявляют себя различным образом, отметим эти различия.

1) В четырехпроводной системе процессы формирования тока в каждой фазе протекают независимо, u_A = e_A = E_m sin q, u_B = e_B = E_m sin(q – 2 p /3), u_C = = e_C = E_m sin(q – 4 p /3. Действующие значения фазных напряжений на нагрузке U_A = U_B = U_C = Е. Токи определяются

I_A = U_A / Z_A,

I_B = U_B / Z_B,

I_C = U_C / Z_C.

2) В трехпроводной системе сумма фазных токов согласно закону Кирхгофа должна быть равна нулю. Это достигается за счет появления ненулевого потенциала средней точки нагрузки относительно средней точки источника u ₀, вектор указанного напряжения обозначим U ₀ . Тогда процессы описываются системой уравнений:

I _A + I _B + I _C = 0,

I_A = (E _A - U₀)/ Z_A,

I_B = (E _B - U₀)/ Z_B,

I_C = (E _C - U₀)/ Z_C.

Из системы уравнений определяем

;

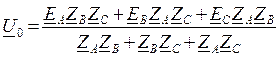U _A= E _A – U ₀;

U _B= E _B – U ₀;

U _C= E _C – U ₀

и находим действующие значения фазных напряжений на нагрузке

Токи определяются выражениями I_A = U_A / Z_A, I_B = U_B / Z_B, I_C = U_C / Z_C.

В любой трехфазной схеме мгновенная мощность в каждой фазе определяется так же, как и в однофазных цепях: p_A = e_A i_A ; p_B = e_A i_B ; p_C = e_C i_C. Мгновенная мощность трехфазной сети равна сумме мгновенных мощностей фаз: p = p_A + p_B + p_C.

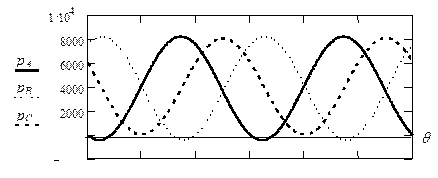
Рассмотрим пример. Трехфазная нагрузка (Z_A = 10+ j ·5 Ом; Z_B = 10 – – j ·5 Ом; Z_C = 12 Ом) питается от симметричной трехфазной сети с нулевым проводом с фазным напряжением 220 В. На рис. 1.9 представлены фазные напряжения на нагрузке u_A, u_B, u_C; фазные токи i_A, i_B, i_C; кривые мгновенных мощностей фаз p_A, p_B, p_C, а также – мгновенная мощность трехфазной системы p.

	Рис. 1.9

Кривая мгновенной мощности p несимметричной трехфазной цепи помимо постоянной составляющей P содержит пульсации с удвоенной частотой сети. Как и в симметричной системе, активная мощность системы равна сумме активных мощностей фаз или среднему значению мгновенной мощности системы на периоде повторения:

P = P_A + P_B +P_C = ,

a реактивная мощность равна сумме реактивных мощностей фаз (с учетом знака реактивной мощности): Q = Q_A + Q_B +Q_C.

Полная (кажущаяся) мощность трехфазной системы равна сумме полных мощностей фаз: S = S_A + S_B + S_C. Коэффициент мощности равен c = =P / S.

Составляющие полной мощности S в рассматриваемом примере приведены в таблице.

Таблица

 

	Фаза А	Фаза В	Фаза С	Трехфазная цепь
Активная мощность, кВт	3,9	3,9		11,8
Реактивная мощность, кВА	1,9	-1,9
Полная мощность, кВА	4,33	4,33		12,6
Мощность несимметрии, кВА		4,7

 

Коэффициент мощности χ = P/S = 0,93. Нетрудно убедиться, что в несимметричной трехфазной цепи P² + Q² ≤ S².

Это означает, что существует еще одна составляющая полной мощности – мощность несимметрии N. Три вектора составляющих полной мощности P, Q и N образуют трехмерную сумму векторов, показанную на рис. 1.10. Мощность несимметрии определяется по формуле

Какова же физическая природа мощности несимметрии?

В рассматриваемом примере реактивная мощность фазы B полностью компенсирует реактивную мощность фазы A и реактивная мощность из сети не потребляется, происходит только взаимообмен реактивной мощностью между фазами A и B. Но реактивные составляющие токов в фазах A и B присутствуют, они увеличивают полную мощность данных фаз и полную мощность трехфазной цепи. Этот процесс внутренней циркуляции реактивных токов в трехфазной нагрузке и отражает мощность несимметрии.

 

 

1.6. Анализ энергетических процессов

методом симметричных составляющих

 

Для анализа процессов в трехфазных цепях широко используется метод симметричных составляющих. Суть метода заключается в том, что любая несимметричная система трех векторов может быть заменена суперпозицией трех симметричных систем сигналов - составляющих прямой, обратной и нулевой последовательности.

Маркируя векторы прямой последовательности I ₁, обратной последовательности I ₂, а нулевой последовательности I ₀, можно представить несимметричную систему токов I_A, I_B, I_C в виде:

I _A = I ₀ + I ₁ + I ₂.

I _A = I ₀ + I ₁· a ² + I ₂· a.

I _A = I ₀ + I ₁ ·a + I ₂·a²,

где - вектор поворота. При умножении векторной величины на а полученныйв результатевектор опережает исходный на 120^о (или отстает на 240^о), при умножении вектора на а ² результирующий вектор опережает исходный на 240^о (или отстает на 120^о).

При использовании метода симметричных составляющих при известных векторах I_A, I_B, I_C из приведенной выше системы уравнений можно найти векторы I ₁, I ₂ и I ₀. А именно

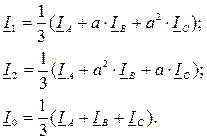
Отметим, что в трехпроводной системе отсутствует нулевая последовательность токов, так как сумма фазных токов равна нулю.

Сосредоточим внимание на энергетических процессах. Используя метод симметричных составляющих, мы будем пользоваться временными зависимостями переменных величин. В трехфазной системе напряжения образуют симметричную систему:

e_A = E_m sin q,

e_B = E_m sin(q – 2 p /3),

e_C = E_m sin(q – 4 p /3.

Токи несимметричны, и их можно представить в виде суммы токов прямой, обратной и нулевой последовательностей:

 

i_A = I 1 _m sin(q – j 1) +I 2 _m sin(q – j 2) + I0_msin(q – j 0);

i_B = I 1 _m sin(q – j 1 – 2 p/ 3) + I 2 _m sin(q – j 2 – 4 p/ 3) +I 0 _m sin(q – j0);

i_C = I 1 _m sin(q – j 1 - 4 p/ 3) + I 2 _m sin(q – j 2 – 2 p/ 3) +I 0 _m sin(q – j0).

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: