 |
Отсюда можно найти величину емкости конденсатора, при которой достигается полная компенсация реактивной мощности сдвига
|
|
|
|
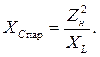
Однако такая полная компенсация достижима лишь при определенной нагрузке. Рассмотрим потребитель, у которого R изменяется от 1 до 10 Ом, а XL всегда 1 Ом. На основе проведенных выше зависимостей рассчитаны и приведены на рис. 1.6 зависимости коэффициента мощности системы c от сопротивления нагрузки при различных значениях реактивного сопротивления конденсатора КРМ: XC = 0,01 Ом (ряд 1), XC = 0,05 Ом (ряд 2), XC = 0,09 Ом (ряд 3), X C = 0,13 Ом (ряд 4), XC = 0,17 Ом (ряд 5),

При малых С полная компенсация достигается лишь при высокоомной нагрузке, при остальных значениях R имеет место недокомпенсация реактивной мощности. При увеличении С область полной компенсации смещается в область меньших сопротивлений нагрузки, причем правее от экстремума (c=1) происходит перекомпенсация, т.е. в сеть выдается емкостная реактивная мощность, которая в ряде случаев может полезно использоваться для компенсации реактивной мощности других потребителей.
Аналогично рассмотрим последовательный КРМ рис. 1.5,б. По-прежнему Z н = R + jXL. Входное сопротивление системы «потребитель энергии – КРМ»
Z = R + j (X L – XC).
Полная компенсация реактивной мощности сдвига достигается при XC посл = XL.
Выполнение этого условия не зависит от R, поэтому при работе на нагрузки, в которых при изменении мощности индуктивная часть входного сопротивления остается неизменной, всегда достижима полная компенсация реактивной мощности.
Сравним значения XC параллельного и последовательного КРМ, рассчитанных на полную компенсацию реактивной мощности потребителя энергии с сопротивлением Z н = R + jXL. Их разность
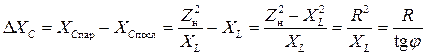 ,
,
всегда положительна. Это означает, что величина емкости в параллельном конденсаторе меньше, причем особенно это проявляется при малых j.
|
|
|
При внезапном коротком замыкании активной части нагрузки в последовательном КРМ образуется последовательный колебательный контур без потерь с резонансом на частоте сети, и нарастание тока короткого замыкания ничем не ограничено. В противоположность этому в параллельном КРМ ток короткого замыкания ограничен индуктивностью нагрузки. В силу этих обстоятельств параллельные КРМ обладают преимуществами.
В общем случае полная компенсация реактивной мощности при применении емкостных компенсаторов при изменении нагрузки недостижима, поэтому получили широкое распространение активные КРМ, содержащие помимо емкостных элементов также мощные полупроводниковые вентили (ключи).
3. Активные компенсаторы реактивной мощности сдвига. Простейшим активным КРМ является устройство рис. 1.7,а, состоящее из набора конденсаторов, отключаемых и подключаемых с помощью полупроводниковых ключей (как правило, однооперационных тиристоров). Схема одного ключа приведена на рис. 1.7,б. Подключение дополнительных емкостных ветвей позволяет ступенчато изменять суммарную емкость параллельного КРМ при изменении мощности нагрузки.
При выборе емкостей комплекта из трех конденсаторов C 1 = C, C 2 = 2 C, C 3 = 4 С, можно получить восемь значений суммарной емкости: 0; С; 2 С; C +2 C =3 C; 4 C; C +4 C =5 C; 2 C +4 C =6 C; C +2 C +4 C =7 C. Таким образом появляется возможность регулировать емкость КРМ с точностью до 14% ее максимального значения.
 |
а) б)
Рис. 1.7
Плавное регулирование реактивной мощности осуществляется в более сложных схемах активных КРМ, которые рассматриваются в специальных курсах.
1.4. Энергетические процессы в симметричных
трехфазных цепях
Обобщенная схема трехфазной сети показана на рис. 1.8. Трехфазная система может быть трехпроводной или «без вывода нейтрали» (нулевой провод, показанный на рис. 1.8 штриховой линией, отсутствует). При этом сумма векторов токов нагрузки равна нулю
|
|
|
IA + IB + IC = 0.
В симметричной четырехпроводной системе («с выводом нейтрали») потенциалы средних точек источника напряжения и нагрузки равны (u 0 = 0) и ток по проводу, показанному на рис. 1.8 пунктиром, не протекает. Соединение нагрузки может быть различным (звезда, треугольник, смешанное соединение разветвленной нагрузки), однако при анализе полагаем, что известными методами электротехники любая нагрузка пересчитана в звезду.
Итак, в симметричной трехфазной системе
ZA = ZB = ZC = Z.
Напряжения образуют симметричную систему синусоид:
uA = eA = U sin q,
uB = eB = U sin(q – 2 p /3),
uC = eC = U sin(q – 4 p /3.
|
|
|


