 |
Модуль внутреннего сопротивления сети равен
|
|
|
|
Zc = 
.
Мощность сети характеризуется отношением модуля тока при коротком замыкании со стороны потребителя I кз = E / Z c к номинальному току потребителя. Если ток короткого замыкания на 3 и более порядков больше номинального тока, то сеть можно считать сетью неограниченной мощности, в противном случае речь идет о сети ограниченной мощности.
Сеть ограниченной мощности не является идеальным источником э.д.с. При протекании тока потребителя на Zc возникает падение напряжения и напряжение u (t) на зажимах токоприемника отличается от э.д.с. e (t). При протекании основной гармоники изменяется величина напряжения, а при протекании токов других гармоник (при нелинейности цепи нагрузки, при больших скачках мощности потребителя) на зажимах токоприемника появляется напряжение, содержащее гармонические составляющие, частота которых отлична от частоты сети.
При наличии нелинейных потребителей в сети ограниченной мощности по сети распространяются созданные ими кондуктивные помехи, гармонические искажения, которые могут мешать работе других потребителей.
При работе трехфазной сети ограниченной мощности на несимметричную нагрузку появляется несимметрия напряжений на зажимах потребителей. Поэтому работа от сети ограниченной мощности означает питание потребителя от источника нестабильного по величине, несинусоидального и - в случае трехфазной сети - несимметричного напряжения. Все эти отклонения напряжения сети от идеальных параметров должны находиться в пределах требований к показателям качества электроэнергии, изложенным в § 3.5.
В гл. 1 и 2 показано, что причины снижения качества электрической энергии сети - это нелинейные, нестационарные и несимметричные нагрузки, причем существенную роль играют как мощные потребители, так и большая совокупность маломощных потребителей с одинаковым режимом работы (например, множество маломощных выпрямителей с емкостным фильтром, см. § 2.2).
|
|
|
Перечислим основные источники искажений величины и формы напряжения сетей ограниченной мощности общего назначения:
1. Силовые полупроводниковые преобразователи. Единичная мощность преобразовательных установок достигает сотен МВт. Как показано в гл. 2, преобразователи потребляют из сети несинусоидальный ток, основная гармоника которого при фазовом управлении имеет фазовый сдвиг относительно напряжения, поэтому они преобразователи реактивную мощность сдвига и генерируют мощность искажений. Одной из основных задач силовой электроники является повышение коэффициента мощности преобразователей и ослабление негативного влияния на показатели качества электрической сети.
2. Дуговые электропечи мощность которых достигает десятков и сотен МВт. Причиной несинусоиальности потребляемого тока является нелинейность вольамперной характеристики электрической дуги и флуктуации при ее горении.
3. Установки электродуговой сварки, питающиеся через выпрямители.
4. Мощные однофазные потребители, непосредственно подключаемые к трехфазной сети.
5. Нестационарные нагрузки большой мощности, включение и выключение которых, а также резкое изменение мощности приводит к появлению несинусоидальных токов.
Источники мощности искажений делятся на источники канонических и неканонических (аномальных) гармоник. К каноническим гармоникам в однофазных сетях относятся все нечетные гармоники. В трехфазных сетях из этого перечня необходимо исключить гармоники, кратные трем, которые отсутствуют в симметричных режимах, т.е. в трехфазных сетях каноническими являются гармоники с номерами n = 1, 5, 7, 11, 13, 17, 19 и т.д.
|
|
|
Источниками неканонических гармоник являются все потребители, обладающие несимметрией полуволн тока: спектр потребляемого тока содержит в этом случае четные гармоники. Источниками неканонических гармоник в трехфазных сетях ограниченной мощности являются несимметричные нагрузки, токи которых содержат гармоники, кратные трем. Наконец, все нестационарные нагрузки, энергопотребление которых резко меняется в процессе работы, потребляют ток, богатый неканоническими гармониками, причем они могут быть расположены как выше, так и ниже частоты сети.
Особенности работы от сети ограниченной мощности сильно проявляются в автономных системах электропитания: на транспортных средствах, в системах с автономным источником энергии (например, дизель-генератором). Нередко в таких системах необходимо применять оборудование (в том числе и устройства силовой электроники), рассчитанные на эти специфические режимы работы.
Другой специфической сетью ограниченной мощности является выходная сеть полупроводниковых преобразователей – источников переменного тока. Выходное напряжение преобразователя, как правило, обладает богатым гармоническим составом, а мощность преобразователя соизмерима с мощностью нагрузки.
При работе от несинусоидальной сети положения Теории мощности, сформулированные в гл. 1 и 2 нуждаются в уточнениях и дополнениях.
3.2. Составляющие полной мощности
при питании линейной нагрузки
Рассмотрим схему рис. 3.2.
Пусть напряжение сети содержит совокупность канонических (нечетных) гармоник
Комплексное сопротивление нагрузки для k -й гармоники обозначим z k, его модуль и фазу
В случае последовательной RL цепи
Ток нагрузки также состоит из суммы канонических гармоник:
Мгновенная мощность может быть представлена в виде двух составляющих:
p * – это сумма произведений токов и напряжений одной и той же частоты;
p ** - сумма произведений токов и напряжений разных частот:
(3.1)
Мгновенная мощность p * равна
(3.2)
где
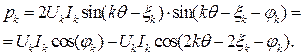(3.3)
Таким образом, каждая из мгновенных мощностей pk содержит постоянную составляющую и имеет переменную составляющую, обуславливающую пульсацию с частотой 2 kf сети. Для каждой гармоники процессы аналогичны работе синусоидальной сети на линейную нагрузку (см. § 1.2).
|
|
|
На каждой из гармоник передается активная мощность
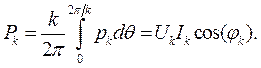(3.4)
и реактивная мощность
(3.5)
Составляющая мгновенной мощности p ** представляет собой сумму произведений колебаний двух частот, в результате умножения которых не возникает постоянной составляющей. Таким образом, составляющая p ** характеризуется мощностью искажения.
При работе несинусоидальной сети на линейную нагрузку полная мощность определяется
. (3.6)
Составляющими полной мощности являются:
· активная мощность, равная сумме активных мощностей гармоник
|
|
|
(3.7)
· реактивная мощность, равная сумме реактивных мощностей гармоник, причем каждая из составляющих может иметь различный знак (для LCR -нагрузок)
|
(3.8)
· мощность искажения
(3.9)
Коэффициент мощности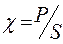 
.
Следует обратить внимание, что выражение 
при питании от несинусоидальной сети несправедливо, и понятие коэффициент искажения не используется.
Для иллюстрации описанных процессов рассмотрим численный пример. На рис. 3.3 приведены временные диаграммы при питании последовательной RL -цепи (R = 1 Ом, L = 0,125 мГн) от источника несинусоидального напряжения u = 100 sin θ + 30· ·sin(3 θ) с основной частотой 1кГц. Результаты расчета составляющих полной мощности приведены в таблице 3.1.
Таблица 3.1
|
| На 1-й Гармонике | На 3-й гармонике | Всего | |
| P, кВт | 3,75 | 0,13 | 3,88 |
| Q, кВА | 1,18 | 0,12 | 1,3 |
| T, кВА | – | – | 0,7 |
| S, кВА | - | - | 4,15 |
| χ | – | – | 0,935 |
Рис. 3.3
3.3. Составляющие полной мощности
при питании нелинейной нагрузки
При работе несинусоидальной сети на нелинейную нагрузку напряжение ток и сети представляют собой суммы гармоник. Принципиальных отличий в энергетических процессах от рассмотренного в § 3.2 режима работы на линейную нагрузку нет. Оперируя величинами тока и напряжения сети, можно провести вычисления составляющих полной мощности по формулам (3.1) – (3.9).
В качестве примера рассмотрим работу однофазного мостового выпрямителя с фазовым управлением (см. § 2.3) от несинусоидальной сети, форма сетевого напряжения прямоугольной формы представлена на рис. 3.4,а. Такой режим работы выпрямителя имеет место, если он получает энергию от силового преобразователя – инвертора напряжения. Схема представлена на рис. 2.7.
|
|
|
Разложение в ряд Фурье e (t)
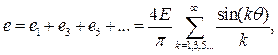
где E – действующее значение e, причем E = Em.
Напряжение на выходе выпрямителя ud (рис. 3.4,б) по-прежнему составлено из отрезков напряжения сети e, на интервале 
ток проводят ключи V 1 и V 2, ud = e, id = i 0. На интервалах 
проводят V 3 и V 4, ud = – e, id = – i 0. Среднее значение выходного напряжения
Ud = 
Ток нагрузки Id(t) = Id =Ud / R представлен на рис. 3.4,б. Ток i 0 (рис. 3.4,а) имеет прямоугольную форму, такую же, как при питании выпрямителя от синусоидальной сети.
Кривые мгновенной мощности на входе и выходе преобразователя совпадают, они повторяют форму ud. Эти кривые приведены на рис. 3.4,в:
Периодом повторения этой функции является половина периода, поэтому активная мощность, выделяемая в нагрузке, может быть найдена путем усреднения на половине периода
P = 
Она же равна активной мощности на входе преобразователя. Мощность, выделяемая на постоянной составляющей Pd = Ud·Id = P. Таким образом, выделение мощности на переменной составляющей в нагрузке отсутствует.
|
Рис. 3.4
Полная мощность S = E · I 0. Коэффициент мощности
Проиллюстрируем формирование составляющих полной мощности. Из разложения в ряд Фурье сетевых напряжения e и тока i 0 выделим первую и третью гармоники, которые приведены на диаграммах рис. 3.4,г и д соответственно. На этих же диаграммах приведены кривые мгновенных мощностей
Эти кривые имеют такой же вид, как при работе синусоидальной сети на комплексную нагрузку. Активные мощности, передаваемые по первой и третьей гармоникам сетевого тока, равны
В представленном на диаграммах рис. 3.4 режиме α = π/6, при этом кривая мгновенной мощности p 3 не содержит постоянной составляющей, поэтому P 3 = 0.
Суммарная активная мощность, передаваемая на всех гармониках,
а реактивная мощность
Мощность искажения 
Зависимости коэффициента мощности χ и коэффициентов KQ и KT от угла задержки включения α приведены на рис. 3.5,а.
|
|
Сравним эти зависимости с кривыми рис. 3.5,б, которые рассчитаны для выпрямителя, питающегося от синусоидальной сети. В рассматриваемом режиме меняются лишь количественные соотношения, но по-прежнему активная мощность падает до нуля при α → 90о(при этом Ud = 0), реактивная мощность достигает своего максимального значения. Иной вид имеет и зависимость мощности искажения.
|
|
|
Увеличение отношения выходного напряжения выпрямителя при α = 0 к действующему значению напряжения сети объясняется тем, что сеть передает активную мощность в нагрузку не только на первой гармонике, но и на высших гармонических составляющих. При работе несинусоидальной сети на выпрямитель этот факт не приводит к негативным последствиям.
Однако передача активной мощности на высших гармониках для ряда линейных и нелинейных нагрузок сетей является нежелательной.
3.4. Работа трехфазной нагрузки от сети
ограниченной мощности
Результаты проведенного анализа можно распространить и на трехфазные нагрузки. Рассмотрим энергетические процессы в характерных режимах.
3.4.1. Симметричная несинусоидальная сеть с симметричной нагрузкой. В этом случае процессы в каждой фазе нагрузки протекают аналогично, отличаясь только сдвигом по фазе. Для одной фазы определяют (в соответствии с методикой § 2.3) полную мощность фазы S ф и ее составляющие – активную и реактивную мощности, а также мощность искажения: P ф, Q ф, T ф, а также коэффициент мощности χ ф. Для трехфазной цепи S = 3 S ф; P = 3 P ф; Q = 3 Q ф; T = 3 T ф. Коэффициент мощности χ = χ ф.
3.4.2. Несимметричная синусоидальная сеть с линейной нагрузкой. При приложении несимметричной системы трехфазных напряжений uA, uB, uC к трехфазной нагрузке, в том числе и к симметричной, протекают несимметричные токи iA, iB, iC, сдвинутые относительно соответствующих фазных напряжений на углы φА, φB и φC. Полная мощность трехфазной цепи определяется известными зависимостями (см. § 1.5) S = UA·IA + UB·IB + + UC·IC; активная мощность P = UA·IA · cos φA + UB·IB cos φB + UC·IC cos φC; реактивная мощность Q = UA·IA sin φA + UB·IB sin φB + UC·IC sin φC; мощность несимметрии 
Коэффициент мощности 
3.4.3. Несимметричная несинусоидальная сеть. Определяем гармонический состав приложенных к фазам нагрузки напряжений и их действующие значения UA, UB , UC . На основе электрического расчета линейной или нелинейной схемы определяем фазные токи, находим их гармонический состав и действующие значения IA, IB , IC . Определяем полную мощность S = UA ·IA + UB ·IB + UC ·IC. Далее находим ее составляющие, суммируя соответствующие значения мощностей, определенные для каждой гармоники (с номером k):
активная мощность
P = 
(UAk·IAk · cos φAk + UBk ·IBk cos φBk + UCk·ICk cos φCk);
реактивная мощность
Q =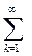 
(UAk ·IAk sin φA + UBk·IBk sin φBk + UCk ·ICk sin φCk);
Обмен реактивной мощностью между фазами несимметричной нагрузки может происходить на всех гармонических составляющих и обуславливает появление мощности искажения N.
При нелинейной нагрузке в системе возникает мощность искажения T.
Таким образом, мощность включает теперь четыре ортогональные составляющие
Рассмотрение достаточно сложных методов расчета мощности несимметрии N и мощности искажения T в данной системе выходит за рамки данного пособия.
Коэффициент мощности
При проведении подобных расчетов используют пакеты прикладных программ для расчета ключевых цепей.
3.5. Нормативы на показатели качества
электрической энергии
Идеальная сеть переменного тока с значительной мере является абстракцией. Повышение качества напряжения сети требует значительных затрат, поэтому необходимо установить некоторые численные параметры, которые регламентировали бы требования к энергоснабжающей организации. С другой стороны при разработке устройств (в том числе и устройств силовой электроники), являющихся потребителями электрической энергии, необходимо учитывать допускаемую стандартом неидеальность сети и обеспечить работоспособность устройств при питании от такой сети.
Для нормирования качества электрической энергии (КЭ), поставляемой энергоснабжающей организацией установлены государственные и отраслевые стандарты. Межгосударственный стандарт СНГ ГОСТ 13109-97 [7] устанавливает нормы качества электрической энергии в сетях общего назначения.
Ниже рассмотрены основные нормативы ГОСТ13109-97 для низковольтных сетей до 1 кВ.
Установлены два вида норм КЭ: нормально допустимые и предельно допустимые. Наибольшие и наименьшие значения параметров КЭ должны находиться в интервале, ограниченном предельно допустимыми значениями. С вероятностью 95 % в течение суток верхнее и нижнее значения показателей КЭ должны находиться в интервале, ограниченном нормально допустимыми значениями.
Показателями КЭ являются:
1) Установившееся отклонение напряжения dU y - изменения напряжения сети, протекающие со скоростью не более 1% в секунду. Нормально допустимые и предельно допустимые значения dU y на выводах приемников электрической энергии равны соответственно ±5 и ±10 % от номинального напряжения электрической сети.
2) Колебания напряжения с большей частотой изменения характеризуются размахом изменения напряжения dUt и дозой фликера. Фликер - субъективное восприятие человеком колебаний светового потока светотехнических приборов, вызванные колебанием напряжения. Предельно допустимое значение суммы установившегося отклонения напряжения dU y и размаха изменений напряжения dU t в точках присоединения к электрическим сетям равно ± 10% от номинального напряжения.
3) Показатели, характеризующие несинусоидальность сети:
А) Коэффициент искажения синусоидальности кривой напряжения - отношение действующего значения высших гармонических составляющих сетевого напряжения Un к действующему значению основной гармоники U ном:
Kн.с.U % = 
100,
где n - номера гармоник. Значения коэффициента искажения: нормально допустимое значение 8%, предельно допустимое значение 12%.
Б) Коэффициент n-ой гармонической составляющей напряжения
KU(n) % = 100 U n / U ном.
Допустимые значения коэффициента приведены в таблице 3.2.
Таблица 3.2
| Нечетные гармоники, не кратные трем | Нечетные гармоники, кратные трем | Четные гармоники | |||
| n | %% | N | %% | n | %% |
| 6,0 | 5,0 | 2,0 | |||
| 5,0 | 1,5 | 1,0 | |||
| 3,5 | 0,3 | 0,5 | |||
| 3,0 | 0,2 | 0,5 | |||
| 2,0 | >21 | 0,2 | 0,5 | ||
| 1,5 | 0,2 | ||||
| 1,5 | > 12 | 0,2 | |||
| 1,5 | |||||
| > 25 | 0,2+1,3´25/ n |
4. Несимметрия напряжении характеризуется следующими показателями:
А) Коэффициент несимметрии напряжений по обратной последовательности K 2 U определяется отношением действующего значения напряжения обратной последовательности основной частоты трехфазного напряжения U 2 (1) к номинальному линейному напряжения U ном.лин:
K 2 U %= 100 U 2(1) / U ном.лин.
Б) Коэффициент нулевой последовательности трехфазной четырехпроводной линии (с нейтралью) определяется отношением действующего значения напряжения нулевой последовательности основной частоты U 0(1) к номинальному фазному напряжения U ном.фаз:
K 0 U %= 100 U 0(1) / U ном.фаз.
Нормально допустимое и предельно допустимое значения коэффициента несимметрии напряжений по обратной последовательности равны 2,0 и 4,0 % соответственно. Нормально допустимое и предельно допустимое значения коэффициента несимметрии напряжений по нулевой последовательности равны 2,0 и 4,0 % соответственно.
5.Нормально допустимое и предельно допустимое значения отклонения частоты равны ± 0,2 и ± 0,4 Гц соответственно.
6. Предельно допустимое значение длительности провала напряжения в электрических сетях равно 30 с. Для защиты ответственной электронной аппаратуры от провалов напряжения используют агрегаты бесперебойного питания.
7. Значения коэффициента временного перенапряжения Кпер U в точках присоединения в зависимости от длительности временных перенапряжений D tпер U приведены в таблице 3.3
Табл. 3.3
| D t пер U, c | До 1 | До 20 | До 60 |
| К пер U | 1,47 | 1,31 | 1,15 |
8.Значение коммутационных импульсных перенапряжений при их длительности на уровне 0,5 амплитуды импульса, равной 1000-5000 мкс, равно 4,5 кВ. Для защиты аппаратуры от коммутационных импульсных перенапряжений применяют сетевые фильтры.
ЗАКЛЮЧЕНИЕ
Мы выяснили, что взаимоотношения потребителя электрической энергии с сетью переменного тока обуславливают целый ряд сложных технико-экономических проблем. Особенно остро встают эти проблемы при проектировании и внедрении устройств силовой электроники, которые являются существенно нелинейными элементами электрической схемы. Если в середине XX века проблемы совместимости преобразователей с сетью играли преимущественно академический характер и нередко игнорировались при создании преобразовательных установок, то в настоящее время эти вопросы во многом являются определяющими. Это приводит к существенному обновлению типов и номенклатуры силовых преобразователей, разработке и появлению на рынке новых типов преобразовательных устройств (корректоры коэффициента мощности, активные выпрямители, кондиционеры сети и др.). Многие новые схемные решения удалось реализовать на базе мощных высокочастотных силовых полупроводниковых приборов, разработанных в конце XX века. Для управления такими преобразовательными устройствами широко используются микропроцессорные устройства управления и другие полупроводниковые микросхемы высокого уровня интеграции.
Разработка новых типов полупроводниковых преобразователей и активных сетевых фильтров стимулируется введением новых международных и государственных стандартов, в которых ожесточаются требования к электромагнитной совместимости сети и преобразователя. Процесс обновления силовой электроники в связи с этим в настоящее время происходит особенно интенсивно, и это ставит перед инженерами, специалистами по Промышленной электронике всё новые интересные задачи, решение многих из них связано с непосредственным применением понятий Теории мощности.
Контрольные вопросы и задачи
1. По каким соотношениям вычисляют действующие значения несинусоидальных токов и напряжений?
|
|
|
2. Найти среднее и амплитудное значение напряжений, приведенных на рисунке, если их действующее значение равно 100 В.
3. Что такое мгновенная мощность? Какой физический смысл имеет полярность мгновенной мощности. Как по кривой мгновенной мощности определить активную мощность?
4. От чего зависит знак реактивной мощности при работе на комплексную линейную нагрузку? Какая составляющая тока переносит активную мощность?
5. Для схемы, приведенной на рисунке, построить кривую мгновенной мощности p(t), найти полную мощность S, активную и реактивную мощности P и Q и коэффициент мощности χ. Напряжение сети E = =220 В, частота 50 Гц, R = 10 Ом, XL 1 = 5 j Ом, ХL 2 = 4 j Ом, XC = – 20 j Ом.
6. К сети 220 В 50 Гц подключена нагрузка – последовательная RL -цепь, R = 10 Ом, XL = j 5 Ом. Нагрузка снабжена параллельным КРМ, полностью компенсирующим реактивную мощности сдвига. Найти емкость конденсатора КРМ C. В каких пределах может изменяться R при L =const, чтобы выполнялось условие: коэффициент мощности χ > 0.95?
7. Объяснить принцип действия параллельного и последовательного КРМ. Каковы преимущества и недостатки каждого из этих типов компенсаторов?
8. Какую форму имеет кривая мгновенной мощности при работе на симметричную трехфазную нагрузку, как рассчитываются полная мощность и ее составляющие?
9. К симметричной синусоидальной трехфазной сети с нулевым проводом (U л = 380 В) подключена несимметричная нагрузка соединенная в звезду: ZA = 10 + j 10 Ом, ZB = 10 Ом, ZC = 10 – j5 Ом. Найти составляющие полной мощности и коэффициент мощности. Объяснить причину появления мощности несимметрии.
10. К симметричной синусоидальной трехфазной сети (U л = 380 В) подключена несимметричная нагрузка, соединенная в треугольник: ZAB = 10 + + j 10 Ом, ZBC = 10 Ом, ZCA = 10 – j5 Ом. Найти составляющие полной мощности и коэффициент мощности.
11. К симметричной синусоидальной трехфазной сети без нулевого провода (Uл = 380 В) подключена несимметричная нагрузка, соединенная в звезду: ZA = 10 + j 10 Ом, ZB = 10 Ом, ZC = 0. Найти составляющие полной мощности и коэффициент мощности.
11. К симметричной синусоидальной трехфазной сети без нулевого провода (Uл = 380 В) подключена несимметричная нагрузка, соединенная в звезду: ZA = 10 + j 10 Ом, ZB = 10 Ом, ZC = 
. Найти составляющие полной мощности и коэффициент мощности.
12. Решить задачу 9 для трехфазной сети без нулевого провода.
13. Объяснить принцип метода симметричных составляющих. Какая составляющая токов в несимметричной трехфазной системе переносит активную мощность? Какая составляющая вызывает пульсации мгновенной мощности?
14. Какая составляющая тока переносит активную мощность при работе синусоидальной сети на нелинейную нагрузку? Объяснить связь величины коэффициента искажений ν и мощности искажений T.
15. Каковы технико-экономические издержки при наличии в сети реактивной мощности сдвига и мощности искажения?
16. Найти гармонический состав и коэффициент искажений ν тока iA 0, показанного на рис. 2.6,б.
17. Найти гармонический состав и коэффициент искажений ν тока i 0, показанного на рис. 2.9,а при α = 45о.
|
19. В управляемом выпрямителе по схеме рис. 2.7 выходное напряжение и ток имеют форму, показанную на рисунке.
|
Напряжение сети E = 220 В, R = 10 Ом, индуктивность в цепи нагрузки велика. Построить временные диаграммы интервалов проводимости ключей, e (θ), i 0(θ). Найти средние значения выходного напряжения и тока Ud и Id, коэффициент мощности χ, коэффициент искажения сетевого тока ν, полную мощность S, активную (P) и реактивную (Q) мощности, мощность искажения T.
20. В управляемом выпрямителе по схеме рис. 2.7 напряжение сети и ток i 0 имеют форму, показанную на рисунке.
|
Напряжение сети E = 220 В, R = 10 Ом, индуктивность в цепи нагрузки велика. Построить временные диаграммы интервалов проводимости ключей, ud (θ), i d(θ). Найти средние значения выходного напряжения и тока Ud и Id, коэффициент мощности χ, коэффициент искажения сетевого тока ν, полную мощность S, активную (P) и реактивную (Q) мощности, мощность искажения T.
21. Объясните принцип действия компенсаторов мощности искажения, схемы которых приведены на рис. 2.11,а и 2.14.
22. Нагрузка – параллельное соединение R = 10 Ом, L = 50 мГн. Напряжение сети e = 200· sin(θ)+50·sin(5 θ), основная частота 50 Гц. Построить кривую мгновенной мощности p (θ), найти полную мощность S и ее составляющие: P, P 1, P 5, Q, Q 1, Q 5, Т, коэффициент мощности χ.
23. Выпрямитель по схеме рис. 2.7 с фазовым управлением связан с сетью e = 200· sin(θ)+50·sin(5 θ), основная частота 50 Гц. Угол задержки включения α = 45о. Сопротивление нагрузки R = 20 Ом, сопротивление индуктивности велико. Построить временные диаграммы e, ud, i 0, id, мгновенной мощности. Найти средние значения выходного напряжения и тока Ud и Id, коэффициент мощности χ, полную мощность S, активную (P) и реактивную (Q) мощности, мощность искажения T.
24. Выпрямитель по схеме рис. 2.7 с широтным управлением связан с сетью e = 500· sin(θ)+150·sin(3 θ), основная частота 50 Гц, α = 30о. Сопротивление нагрузки R = 20 Ом, сопротивление индуктивности велико. Построить временные диаграммы e, ud, i 0, id. Найти средние значения выходного напряжения и тока Ud и Id, коэффициент мощности χ, полную мощность S, активную (P) и реактивную (Q) мощности, мощность искажения T.
25. Какие показатели качества характеризуют несинусоидальность сети? Почему выпрямители влияют на несинусоидальность сети ограниченной мощности?
26. При каких нагрузках ухудшаются показатели несимметрии сети K 2 U и K 0 U?
27. Какие устройства улучшают показатели качества по несинусоидальности напряжения? Опишите принцип дейcтвия этих устройств.
Библиографический список
1. Маевский О.А. Энергетические показатели вентильных преобразователей. – М. Энергия, 1978. – 320 с.
2. Супронович Г. Улучшение коэффициента мощности преобразовательных установок: пер. с польск.. – М.: Энергоатомиздат, 1985. – 136 с.
3. Горбачев Г.Н., Чаплыгин Е.Е. Промышленная электроника: учебник для вузов. - М.: Энергоатомиздат, 1988. – 320 с.
4. Попков О.З. Основы преобразовательной техники. Неуправляемые выпрямители. - М.: Издательство МЭИ, 2001. – 64 с.
5. Попков О.З. Основы преобразовательной техники. Управляемые выпрямители. - М.: Издательство МЭИ, 2001. – 48 с.
6. Попков О.З. Основы преобразовательной техники. Автономные преобразователи. - М.: Издательство МЭИ, 200. – 64 с.
7. ГОСТ 13109-97. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах общего назначения. – М.: Из-во стандартов. 2000.
|
|
|
