Методика выполнения задания 1

При выполнении первого задания рассчитываются показатели описательной статистики. Для этого используются следующие формулы.

1. Выборочное среднее,

,

где – измеренная величина;

– количество измеренных значений.

Выборочное среднее характеризует среднее значение экспериментального показателя в выборке наблюдений. Этот показатель очень часто используется при сравнении различных выборок наблюдений. Пусть в результате эксперимента получена выборка значений: 3, 2, 1, 0, 3, 2, 3. Рассчитаем ее выборочное среднее

2. Выборочная дисперсия,

Выборочная дисперсия характеризует меру рассеивания случайной величины относительно математического ожидания (выборочного среднего значения).

Выборочная дисперсия в условиях предыдущего примера рассчитывается как

3. Выборочная медиана, p_0.5

Выборочная медиана представляет собой то значение в вариационном ряду, которое делит его пополам. Например, в вариационном ряду всего 21 измерение, поэтому значение 11-го измерения и будет значением медианы. Этот показатель очень часто используется в психологических исследованиях.

4. Ассиметрия, А

В том случае, если А < 0, то эмпирическое распределение несимметрично и сдвинуто вправо. При А > 0 распределение имеет сдвиг влево. При А = 0 распределение симметрично.

 

5. Эксцесс, Е. Показатель, характеризующий выпуклость или вогнутость эмпирических распределений

В том случае, если Е больше или равно нулю, то распределение выпукло, в других случаях вогнуто.

6. Квантиль

Квантиль – то значение вариационного ряда, которое соответствует заданному значению вероятности появления признака. При р = 0,25 это значение называется нижний квартиль, при р = 0,75 – верхний квартиль. Например, в выборке из 13 значений нижний квартиль равен 13, верхний – 25, а мода 21.

 

 

7. Размах выборки, L

Дальнейший этап исследований связан с выяснением вида закона распределения случайных величин, так от результатов этого этапа в значительной степени зависит и схема дальнейшего анализа. Для определения вида закона распределения случайной величины проводят группировку вариационного ряда методом классификации. Сначала определяют количество интервалов (у нас по условию оно равно 6), при этом используют следующее правило: количество интервалов группировки данных примерно в три раза меньше общего количества данных. После этого определяют размер интервала классификации как,

где – максимальное и минимальное значения в выборке;

m – количество интервалов.

Далее определяют границы каждого интервала, начиная от первого значения вариационного ряда , где – нижняя и верхняя границы интервала группирования.

После этого подсчитывают количество измерений, попадающих в каждый интервал, и результаты делят на общее число измерений (определяют частности).

На заключительном этапе строят гистограмму – последовательность столбцов, каждый из которых представляет собой интервал группирования данных, а высота его пропорциональна количеству измерений, попавших в этот интервал (рис. 1). На рисунке видно, что результаты эксперимента группируются по интервалам неравномерно. При этом большая часть измерений попадает в интервал от 2 до 3. Кроме того, на рис.1 показана непрерывная линия предполагаемого закона нормального распределения, построенного по вычисленным характеристикам m_х (математическое ожидание) и d_x. (дисперсия). Так как положение этой линии в значительной степени отличается от экспериментальных данных, можно сделать вывод о том, что эмпирическая (построенная нами) функция распределения не подчиняется нормальному закону распределения.

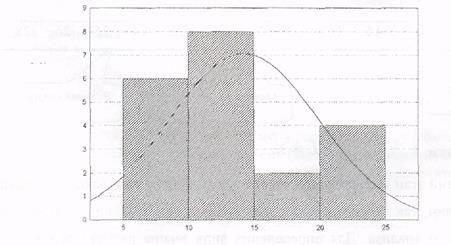
Рис. 1. Гистограмма, построенная по результатам эксперимента

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: