 |
Предельные значения дисбаланса для кругов высотой до 25 мм
|
|
|
|
Предельные значения дисбаланса для кругов высотой до 25 мм
|
Наружный диаметр, мм |
Предельное значение дисбаланса г ∙ мм, в зависимости от его класса | |||
Убедившись в правильности балансировки, эти операции повторяют. Балансировку производят дважды – перед установкой планшайбы с кругом на шпиндель шлифовальной бабки и после предварительной правки по профилю абразивного круга алмазным инструментом.
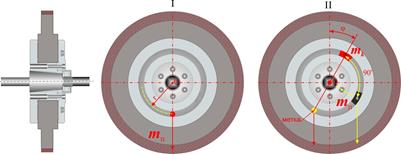
Для балансировки шлифовальных кругов часто используют метод подбора корректирующей массы по отклонению метки, который заключается в установке ее на месте, диаметрально противоположном положению центра масс ротора.
Величина корректирующей массы 
определяется расчетом. Для этого фиксируются два равновесных положения ротора (рис. 10. 4): без пробной массы 
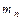(положение I) и с , установленной под углом 90° к «легкому месту» (ЛМ) ротора (положение II).
|
| Рис. 10. 4 Схема определения корректирующей массы методом подбора |
Значение 
определяется из выражения (10. 1):
, (10. 1)
где 
– величина неуравновешенной массы; φ – угол поворота ротора при установке пробной массы.
Величина в зависимости от размеров ротора может достигать значительных величин. Для данного метода существуют готовые номограммы, позволяющие значительно сократить время балансировки.
На практике также используют метод расчета корректирующей массы по колебаниям. Метод заключается в измерении периодов колебани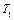й 
и 
ротора, отклоненного на угол φ от положения равновесия без пробной массы 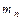и с пробной массой 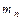, которая устанавливается в «тяжелом месте» (ТМ). Величину корректирующей массы рассчитывают по формуле (10. 2):
|
|
|
. (10. 2)
Периоды колебаний 
и 
оценивают по времени десяти двойных качаний неуравновешенного ротора. Для сокращения времени балансировки используют номограммы.
При динамической неуравновешенности применяют динамическую балансировку. Динамическая неуравновешенность имеет место в том случае, когда центр масс О ротора смещен относительно оси вращения, а главная центральная ось инерции I-I наклонена к оси вращения ротора под углом γ р. Примером динамически неуравновешенного ротора может служить двухколенчатый вал с эксцентрично закрепленным на нем круглым диском (рис. 10. 5).
|
| Рис. 10. 7. Схема двухколенчатого вала с динамической неуравновешенностью |
Опоры А и B нагружены скрещивающимися силами 
и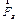 
, векторы которых вращаются вместе с валом. Неуравновешенность ротора количественно выражается через главный вектор дисбаланса 
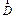и главный момент дисбалансов ротора 
, где 
, 
.
В результате ликвидации динамической неуравновешенности главная центральная ось инерции I-I совмещается с его осью вращения, или аналитически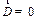 
, 
.
Динамическую неуравновешенность можно устранить двумя корректирующими массами, расположенными в плоскостях коррекции, перпендикулярных оси вращения (рис. 10. 6).
На рис. 10. 6 
и 
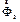– центробежные силы инерции двух сосредоточенных масс 
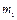и 
. Задача уравновешивания сводится к подбору таких масс противовесов и выбору такого места её установки в плоскостях исправления I и II, чтобы их центробежные силы были равны и противоположно направлены силам инерции.
Неуравновешенность звена в каждой из плоскостей исправления характеризуется величиной дисбалансов:
; 
,
где 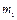и – сосредоточенные массы; 
и 
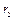– радиусы их расположения.
|
|
|
Очевидно, что противовесы 
и 
должны располагаться противоположно сосредоточенным массам 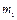и так, чтобы выполнялись условия:
, 
,
где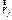 
и 
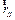– радиусы установки противовесов.
Если придать вращение планшайбе с кругом, то сила инерции неуравновешенной в плоскости I массы , вращаясь, создает момент относительно центра вращения, который будет изменяться по гармоническому закону, так как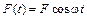 
.
|
| Рис. 10. 6. Схема центробежных сил инерции двух сосредоточенных масс |
При вращении система совершает вынужденные колебания с частотой ω. Благодаря наличию сил трения угловая скорость шпинделя станка после отключения двигателя будет убывать и в какой-то момент совпадёт с частотой свободных колебаний системы. Амплитуда колебаний при этом резко возрастет.
Из теории колебаний известно, что при резонансе амплитуда колебаний А пропорциональна величине возмущающей силы. В зависимости от параметров, измеряемых при балансировке, различают методы амплитуд, фаз и одновременного измерения амплитуд и фаз вибраций.
К методам одноплоскостной балансировки относятся методы амплитуд и кругового обхода. Метод амплитуд требует измерения амплитуд 
начальной вибрации при пуске объекта без пробной массы и амплитуд 
при его пусках с пробными массами, устанавливаемыми в определенных положениях на планшайбе. Метод кругового обхода основан на измерении амплитуд вибрации и при пусках шлифовального станка с пробной массой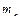 
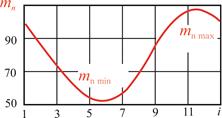
, переставляемой последовательно на равные углы. По данным измерений строят зависимость от положения пробной массы (аналогично рис. 10. 7). Корректируемая масса устанавливается в плоскости (точке расположения) 
, а ее величина определяется по формулам:
, при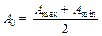 
. (10. 3)
|
| Рис. 10. 7. Кривая зависимости величины пробной массы от точек приложения |
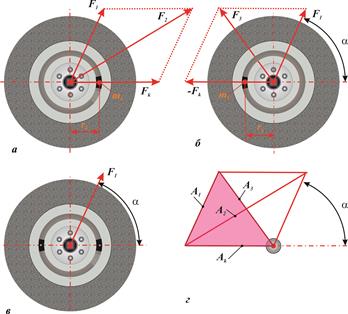
Задача компенсации динамической неуравновешенности также может быть решена методом корректирующих масс (рис. 10. 8), который заключается в следующем.
Если в паз планшайбы установить корректировочный (добавочный) груз с известной массой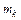 
на известном расстоянии от оси вращения круга 
, то при вращении шпинделя к условной центробежной силе 
добавится сила Fk, зависимая от дисбаланса корректировочного груза. При установке этого груза с противоположной стороны на том же расстоянии, вместо силы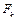 
будет действовать равная ей противоположная сила 
(рис. 10. 8 а, б). Сила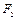 
является суммой векторов и 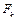. Сила 
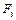является суммой векторов и . Многократно запуская станок и фиксируя амплитуды колебаний при резонансе можно получить средние значения амплитуд в опытах без корректирующего груза, с корректирующим грузом, и с тем же грузом, установленным в противоположной прорези диска.
|
|
|
Предполагая, что эти амплитуды пропорциональны силам, возбуждающим колебания рамы станка при различных опытах, можно математически описать взаимосвязи между амплитудами. Отношения между их величинами можно представить в виде параллелограмма (рис. 10. 8, г), подобного параллелограммам сил (рис. 10. 8 а, б).
Для параллелограмма удвоенная сумма квадратов сторон равна сумме квадратов диагоналей:
. (10. 4)
Отсюда следует, что
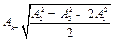. (10. 5)
Вычислив эту амплитуду и предположив, что амплитуды пропорциональны соответствующим им дисбалансам, расположенным в плоскости коррекции, получим:
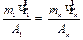. (10. 6)
Дисбаланс ротора, условно отнесенный к плоскости коррекции, можно представить в виде:
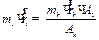. (10. 7)
Это условный эквивалент действительного дисбаланса ротора (его условность связана с приписываемым ему расположением в левой плоскости коррекции). Именно такой дисбаланс должен иметь противовес, располагаемый на противоположной от него стороне оси ротора.
|
| Рис. 10. 8. Схема условных сил в плоскости коррекции (а, б, в) и взаимосвязанных с ними амплитуд (г) |
Его угловое положение по отношению к оси прорезей в корректировочном диске определяется из косоугольного треугольника:
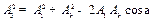. (10. 8)
Отсюда
. (10. 9)
|
|
|
При выполнении балансировки производится 3 опыта:
1) в первом опыте измеряется резонансная амплитуда 
, вызываемая дисбалансом ротора в плоскости I; ;
2) во втором опыте измеряется амплитуда резонанса 
после установки корректирующей массы на расстоянии 
в один из пазов диска в плоскости I (величины и задают произвольно);
3) в третьем опыте измеряется амплитуда резонанса 
после установки той же массы и на том же расстоянии , но в диаметрально противоположном пазу диска.
Параллелограммы амплитуд во втором и третьем опытах равны между собой и в совмещенном виде показаны на рис. 10. 8, г.
Из полученного параллелограмма определяем амплитуду 
, вызываемую добавочной массой и угловое положение дисбаланса (угол a).
Балансировку ротора можно выполнить методом двух пробных пусков. Делается основной пуск установки и замеряется амплитуда колебаний 
. Основываясь на том, что амплитуда вынужденных колебаний пропорциональна дисбалансу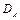 
, справедливо соотношение:
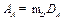, (10. 10)
где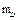 
– коэффициент пропорциональности.
Поскольку коэффициент пропорциональности нам не известен, то делают кроме основного еще два пробных пуска, откуда и берет свое название этот метод.
Перед первым пробным пуском в прорезь диска (на известном расстоянии от оси вращения ротора ) устанавливают корректировочный (добавочный) груз с известной массой , дисбаланс которой равен:
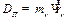. (10. 11)
Делается первый пробный пуск. Теперь колебания с амплитудой будут выражаться моментом суммарного дисбаланса:
, (10. 12)
причем замеренная амплитуда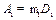 
.
Примечание. В методе «корректирующих масс» не соответствует в методе «двух пробных пусков».
Перед вторым пробным пуском на расстояние (в ту же прорезь диска) устанавливается пробная масса 
, дисбаланс которой удвоится по сравнению с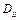 
. Осуществляем второй пробный пуск и замеряем амплитуду колебаний. Тогда справедлива запись:
, (10. 13)
при этом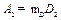 
.
Используя свойства диагоналей параллелограмма (рис. 10. 9), получим модуль дисбаланса :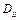
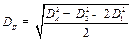(10. 14)
|
| Рис. 10. 9. Схема к балансировке методом «двух пробных пусков» |
Помножив левую и правую части этого уравнения на 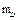, на основании пропорциональности амплитуд и дисбалансов, а также уравнения (10. 8), найдем значение коэффициента пропорциональности :
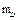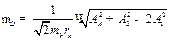. (10. 15)
Из уравнения (10. 7) определяем модуль 
искомого дисбаланса:
|
|
|
. (10. 16)
Для устранения дисбаланса в плоскости необходимо создать дисбаланс, равный по величине, но противоположный по направлению, т. е.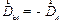 
.
Угол, под которым надо установить корректирующую массу, определим из выражения:
cosjkA 
, (10. 17)
где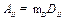 
.
Полученному значению косинуса соответствуют два угла, одинаковых по абсолютной величине, но противоположных по знаку. Верное направление отсчета угла jkA от линии CN неизвестно и его следует определить способом проб.
Метод четырех пробных пусков основан на измерении величин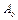 
, 
, 
, 
, 
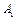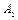при четырех пусках с одинаковой пробной массой 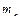, последовательно переставляемой по одному и тому же радиусу на угол 90°. Относительные величины вибраций
; 
; 
; 
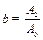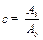(10. 18)
располагают в убывающем порядке: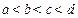 
. Величина корректирующей массы и угол ее установки b определяют из выражений (10. 8):
(10. 19)
|
|
|
