Основные приемы изучения взаимосвязей

Для изучения, измерения и количественного выраже­ния взаимосвязей между явлениями статистикой приме­няются различные методы, такие как: метод сопоставле­ния параллельных рядов, балансовый, графический, ме­тоды аналитических группировок, дисперсионного и кор­реляционного анализа.

Метод параллельных рядов заключается в том, что полученные в результате сводки и обработки материалы располагают в виде параллельных рядов и сопоставляют их между собой для установления характера и тесноты связи.

Балансовый метод состоит в том, что данные взаимо­связанных показателей изображаются в виде таблицы и располагаются таким образом, чтобы итоги между отдель­ными ее частями были равны, т.е. чтобы был баланс. Ба­лансовый метод используется для характеристики взаи­мосвязи между производством и распределением про­дуктов, денежными доходами и расходами населения и т.д. Почти все внутренние и внешние хозяйственные свя­зи выражаются в виде балансов.

Метод аналитических группировок. Сущность метода аналитических группировок состоит в том, что единицы статистической совокупности группируются, как правило, по факторному признаку и для каждой группы рассчиты­вается средняя или относительная величина по результа­тивному признаку. Затем изменения средних или относи­тельных значений результативного признака сопоставляются с изменениями факторного признака для выявления характера связи между ними.

Дисперсионный анализ дает прежде всего возможность определить значение систематической и случайной вариа­ций в общей вариации, а также установить роль интересу­ющего нас фактора в изменении результативного призна­ка.

Для характеристики тесноты корреляционной связи между признаками в аналитических группировках меж­групповую дисперсию сопоставляют с общей. Это сопо­ставление называется корреляционным отношением и обозначается:

(8.5.)

Оно характеризует долю вариации результативного признака, вызванной действием факторного признака, положенного в основание группировки. Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до 1. Чем ближе корреляционное отноше­ние к 1, тем большее влияние оказывает факторный при­знак на результативный. Если же факторный признак не влияет на результативный, то вариация, обусловленная им, будет равна нулю (d ² = 0) и корреляционное отношение также будет равно нулю (h² = 0), что говорит о полном отсутствии связи. И наоборот, если результативный при­знак изменяется только под воздействием одного фактор­ного признака, то вариация, обусловленная этим призна­ком, будет равна общей вариации (h²=h² ) и корреляци­онное отношение будет равно единице (h² = 1), что го­ворит о существовании полной связи.

Дисперсионный анализ позволяет не только опреде­лить роль случайной и систематической вариаций в об­щей вариации, но и оценить достоверность вариации, обнаруженной методом аналитических группировок. Опре­деление достоверности вариации дает возможность с за­данной степенью вероятности установить, вызвана ли меж­групповая вариация признаком, положенным в основание группировки, или она является результатом действия слу­чайных причин. Для оценки существенности корреляци­онного отношения пользуются критическими значениями корреляционного отношения h²при разных уровнях веро­ятности или значимости a.

Уровень значимости — это достаточно малое значе­ние вероятности, отвечающее событиям, которые в дан­ных условиях исследования будут считаться практически невозможными. Появление такого события считается ука­занием на неправильность начального предположения. Чаще всего пользуются уровнями a = 0,05 или a = 0,01. Критические значения корреляционного отношения содержатся в специальных таблицах.

В этих таблицах распределение h² при случайных вы­борках зависит от числа степеней свободы факторной и случайной дисперсии. Число степеней свободы фактор­ной дисперсии равно:

 

К₁=m-1 (8.6.)

 

где m — число групп, а для случайной дисперсии:

K₁=n – m (8.7.)

где п — число вариант; m — число групп.

При проверке существенности связи чаще пользуются критерием Фишера, потому что при больших числах сте­пеней свободы его табличные значения мало изменяются в отличие от корреляционного отношения, которое требу­ет более громоздких таблиц. Критерий Фишера представ­ляет собой отношение межгрупповой дисперсии к сред­ней из внутригрупповых дисперсий, исчисленных с уче­том числа степеней свободы:

(8.8)

Для этих отношений составляются таблицы, по кото­рым можно определить, какая величина F при данном числе степеней свободы по факторной вариации (K₁) и остаточной вариации (К₂ ) дает основание утверждать с определенной вероятностью (например, 0,95; 0,99), что положенный в основание группировки признак является существенным, или не дает такого основания, и, следо­вательно, группировочный признак является несуществен­ным.

Зная корреляционное отношение, можно определить критерий Фишера по следующей формуле:

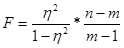(8.9.)

Подобный дисперсионный анализ может проводиться при группировке по одному факторному признаку или при комбинационной группировке по двум и более факторам.
В таком случае необходима оценка достоверности влияния не только каждого положенного в основание группировки фактора в отдельности, но и результата их взаимо­действия. Последний определяется как разность между эффектом совместного влияния двух группировочных признаков и суммой эффектов влияния каждого из этих факторных признаков, взятых в отдельности. Это осложняет расчеты суммы квадратов отклонений и числа степеней свободы вариации. Но сам принцип дисперсионного анализа, основанный на сопоставлении факторной дисперсии со случайной для оценки достоверности результатов ста­тистической группировки, остается применим независимо от числа признаков группировки.

Корреляционный анализ

Корреляционный анализ решает две основные задачи.

Первая задача заключается в определении формы свя­зи, т.е. в установлении математической формы, в кото­рой выражается данная связь. Это очень важно, так как от правильного выбора формы связи зависит конечный ре­зультат изучения взаимосвязи между признаками.

Вторая задача состоит в измерении тесноты, т.е. меры связи между признаками с целью установить степень вли­яния данного фактора на результат. Она решается мате­матически путем определения параметров корреляцион­ного уравнения.

Затем проводятся оценка и анализ полученных резуль­татов при помощи специальных показателей корреляци­онного метода (коэффициентов детерминации, линейной и множественной корреляции и т.д.), а также проверка существенности связи между изучаемыми признаками.

Определяющая роль в выборе формы связи между явлениями принадлежит теоретичес­кому анализу. Так, например, чем больше размер основ­ного капитала предприятия (факторный признак), тем боль­ше при прочих равных условиях оно выпускает продук­ции (результативный признак). С ростом факторного при­знака здесь, как правило, равномерно растет и результа­тивный, поэтому зависимость между ними может быть выражена уравнением прямой Y = а₀ + а₁ x, которое назы­вается линейным уравнением регрессии.

Параметр а₁ называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу. При х=0 а₀ = Y. Увеличение количества внесенных удобрений приводит, при прочих равных условиях, к росту урожайности, но чрезмерное внесение их без изменения других элементов к дальнейшему повышению урожайности не приводит, а, наоборот, снижает ее. Такая зависимость может быть вы­ражена уравнением параболы Y = а₀ + а₁ x + а₂ x^2..

Параметр а₂ характеризует степень ускорения или за­медления кривизны параболы, и при а₂ > 0 парабола име­ет минимум, а при а₂ < 0 — максимум. Параметр а₁ ха­рактеризует угол наклона кривой, а параметр а₀ — начало кривой.

Однако с помощью теоретического анализа не всегда удается установить форму связи. В таких случаях прихо­дится только предполагать о наличии определенной фор­мы связи. Проверить эти предположения можно при по­мощи графического анализа, который используется для выбора формы связи между явлениями, хотя графический метод изучения связи применяется и самостоятельно.

Применение мето­дов корреляционного анализа дает возможность выражать связь между признаками аналитически — в виде уравне­ния — и придавать ей количественное выражение. Рас­смотрим применение приемов корреляционного анализа на конкретном примере.

Допустим, что между стоимостью основного капитала и выпуском продукции существует прямолинейная связь, которая выражается уравнением прямой Y = а₀ + а₁ x. Не­обходимо найти параметры а₀ и a₁ что позволит опреде­лить теоретические значения Y для разных значений х. Причем а₀ и a₁ должны быть такими, чтобы было достиг­нуто максимальное приближение к первоначальным (эм­пирическим) значениям теоретических значений Y. Эта за­дача решается при помощи способа наименьших квадра­тов, основное условие которого сводится к определению параметров а₀ и a₁ таким образом, чтобы å (у_i - Y) ² = min.

Математически доказано, что условие минимума обеспе­чивается, если параметры а₀ и a₁ определяются при помо­щи системы двух нормальных уравнений, отвечающих требованию метода наименьших квадратов:

åy=na₀ +a₁åx

åxy=a_0*åx ² (8.10)

Первое уравнение есть сумма всех первоначальных уравнений. Второе получается умножением обеих частей уравнения прямой на один и тот же множитель. Математически доказано, что условие å (у_i - Y) ² = min соблюдается, если в качестве такого множителя принять значе­ние факторного признака, т.е. если уравнение прямой умножить на x.

Кроме рассмотренных функций связи в экономичес­ком анализе часто применяются степенная, показательная и гиперболическая функции.

Степенная функция имеет вид Y = а₀ х^а1. Параметр a₁ степенного уравнения называется показателем эластично­сти и указывает, на сколько процентов изменится у при возрастании х на 1 %. При х = 1 а₀ =. Y.

Для определения параметров степенной функции вна­чале ее приводят к линейному виду путем логарифмиро­вания: l g y = lg a₀ + а₁ lg x₁, а затем строят систему нор­мальных уравнений:

(8.11)

Решив систему двух нормальных уравнений, находят логарифмы параметров логарифмической функции а₀ и а₁ а затем и сами параметры а₀ и а₁ При помощи степенной функции определяют, например, зависимость между фондом заработной платы и выпуском продукции, затратами труда и выпуском продукции и т.д.

Если факторный признак x растет в арифметической про­грессии, а результативный у — в геометрической, то такая зависимость выражается показательной функцией Y = а_{0 *} а₁ ². Для определения параметров показательной функции ее так­же вначале приводят к линейному виду путем логарифми­рования: lg у = lg а₀ + х lg a₁, а затем строят систему нор­мальных уравнений:

(8.12)

Вычислив соответствующие данные и решив систему двух нормальных уравнений, находят параметры показа­тельной функции а_о и а_1.

В ряде случаев обратная связь между факторным и результативным признаками может быть выражена урав­нением гиперболы:

(8.13)

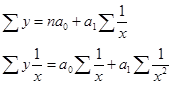И здесь задача заключается в нахождении параметров а₀ и a_t при помощи системы двух нормальных уравнений:

(8.14)

При помощи гиперболической функции изучают, на­пример, связь между выпуском продукции и себестоимо­стью, уровнем издержек обращения (в % к товарообороту) и товарооборотом в торговле, сроками уборки и урожай­ностью и т.д.

Таким образом, применение различных функций в ка­честве уравнения связи сводится к определению парамет­ров уравнения по способу наименьших квадратов при по­мощи системы нормальных уравнений.

В малых совокупностях значение коэффициента рег­рессии подвержено случайным колебаниям. Поэтому воз­никает необходимость в определении достоверности ко­эффициента регрессии. Достоверность коэффициента ре­грессии определяется так же, как и в выборочном наблю­дении, т.е. устанавливаются средняя и предельная ошиб­ки для выборочной средней и доли. Средняя ошибка коэффициента регрессии определяется по формуле:

(8.15)

где s₀² — случайная дисперсия; s ²— общая дисперсия, п - число коррелируемых пар.

Измерение тесноты связи

Чтобы измерить тесноту прямолинейной связи между двумя признаками, пользуются парным коэффициентом корреляции, который обозначается r

Так как при корреляционной связи имеют дело не с приращением функции в связи с изменением аргумента, а с сопряженной вариацией результативных и факторных признаков, то определение тесноты связи, по существу, сводится к изучению этой сопряженности, т.е. того, в ка­кой мере отклонение от среднего уровня одного признака сопряжено с отклонением другого. Это значит, что при наличии полной прямой связи все значения (х —X) и (у — Y) должны иметь одинаковые знаки, при полной обратной — разные, при частичной связи знаки в преобладающем чис­ле случаев будут совпадать, а при отсутствии связи — совпадать примерно в равном числе случаев.

Для оценки существенности коэффициента корреляции пользуются специально разработанной таблицей критичес­ких значений г.

Коэффициент корреляции r_xy. применяется только в тех случаях, когда между явлениями существует прямолиней­ная связь.

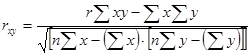(8.16.)

Если же связь криволинейная, то пользуются индексом корреляции, который рассчитывается по форму­ле:

(8.17)

где у — первоначальные значения; — среднее значение; Y— теоретические (выравненные) значения переменной величины.

Показатель остаточной, случайной дисперсии опреде­ляется по формуле:

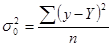
(8.18)

Она характеризует размер отклонений эмпирических значений результативного признака y от теоретических Y, т.е. случайную вариацию.

Общая дисперсия

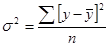
(8.19)

характеризует размер отклонений эмпирических значений результативного признака у от , т.е. общую вариацию. Отношение случайной дисперсии к общей характеризует долю случайной вариации в общей вариации, а

(8.20.)

есть не что иное, как доля факторной вариации

(8.21)

в общей, потому что по правилу сложения дисперсий об­щая дисперсия равна сумме факторной и случайной дис­персий:

s=s_Y²+s₀² (8.22)

Подставим в формулу индекса корреляции соответству­ющие обозначения случайной, общей и факторной дис­персий и получим:

 

(8.23)

Таким образом, индекс корреляции характеризует долю факторной вариации в общей:

(8.24)

однако с той лишь разницей, что вместо групповых сред­них берутся теоретические значения Y.

Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости случайная вариация å(y-Y)²=0, индекс корреляции равен 1. При отсутствии связи R = 0, потому что Y = у.

Коэффициент корреляции является мерой тесноты связи только для линейной формы связи, а индекс корреля­ции — и для линейной, и для криволинейной. При прямо­линейной связи коэффициент корреляции по своей абсо­лютной величине равен индексу корреляции:

(8.25)

 

Если индекс корреляции возвести в квадрат, то полу­чим коэффициент детерминации

(8.26)

Он характеризует роль факторной вариации в общей вариации и по построению аналогичен корреляционному отношению з². Как и корреляционное отношение, коэф­фициент детерминации R² может быть исчислен при по­мощи дисперсионного анализа, так как дисперсионный анализ позволяет расчленить общую дисперсию на фак­торную и случайную. Однако при дисперсионном анализе для разложения дисперсии пользуются методом группи­ровок, а при корреляционном анализе — корреляционны­ми уравнениями.

Коэффициент детерминации является наиболее конк­ретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, поло­женного в основание группировки.

При прямолинейной парной связи факторную диспер­сию можно определить без вычисления теоретических зна­чений Y по следующей формуле:

(8.27)

Множественная корреляция

До сих пор мы рассматривали корреляционные связи между двумя признаками: результативным (у) и фактор­ным (х). Например, выпуск продукции зависит не только от размера основного капитала, но и от уровня квалифи­кации рабочих, состояния оборудования, обеспеченности и качества сырья и материалов, организации труда и т.д. В связи с этим возникает необходимость в изучении, из­мерении связи между результативным признаком, двумя и более факторными. Этим занимается множественная корреляция.

Множественная корреляция решает три задачи. Она определяет:

1) форму связи;

2) тесноту связи;

3) влияние отдельных факторов на общий результат.

Определение формы свя­зи сводится обычно к отысканию уравнения связи у с фак­торами x,z,w,...у. Так, линейное уравнение зависимости результативного признака от двух факторных определяет­ся по формуле

(8.28)

Для определения параметров а₀, а_} и а₂, по способу наименьших квадратов необходимо решить следующую систему трех нормальных уравнений:

(8.29.)

При определении тесноты связи для множественной зависимости пользуются коэф­фициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреля­ции. Так, при изучении связи между результативным признаком у и двумя факторными признаками — х и z, нужно предварительно определить тесноту связи между у и х, между у и z, т.е. вычислить коэффициенты парной кор­реляции, а затем для определения тесноты связи резуль­тативного признака от двух факторных исчислить коэф­фициент множественной корреляции по следующей фор­муле:

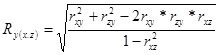(8.30.)

где r_xy, r_zy, r_xz — парные коэффициенты корреляции.

Коэффициент множественной корреляции колеблется в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный резуль­тат.

Если коэффициент множественной корреляции возве­сти в квадрат, то получим совокупный коэффициент де­терминации, который характеризует долю вариации резуль­тативного признака у под воздействием всех изучаемых факторных признаков.

Совокупный коэффициент детерминации, как и при парной корреляции, можно исчислить по следующей фор­муле:

(8.31)

где — дисперсия факторных признаков, 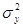— диспер­сия результативного признака. Однако вычисление теоретических значений Y при множественной корреляции и сложно, и громоздко. Поэтому факторную дисперсию исчисляют по следующей формуле:

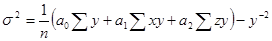(8.32)

 

Проверка существенности связи при множественной корреляции, по сути, ничем не отличается от проверки при парной корреляции.

Поскольку факторные признаки действуют не изоли­рованно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным при­знаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных ко­эффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между х и у при по­стоянном z рассчитывается по следующей формуле:

(8.33)

В настоящее время на практике широкое распростра­нение получил многофакторный корреляционный анализ.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: