Методы измерения тесноты связи

Измерение тесноты связи при помощи дисперсионно­го и корреляционного анализа связано с определенными сложностями и требует громоздких вычислений. Для ори­ентировочной оценки тесноты связи пользуются прибли­женными показателями, не требующими сложных, тру­доемких расчетов. К ним относятся: коэффициент кор­реляции знаков Фехнера, коэффициент корреляции ран­гов, коэффициент ассоциации и коэффициент взаимной сопряженности.

Коэффициент корреляции знаков основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков, а не на сопоставлении попарно размеров отклонений индивидуальных значений факторного и результативного признаков от средней (х— х) и (у — у):

(8.34)

где и — число пар с одинаковыми знаками отклонений х и у от х и у; v — число пар с разными знаками отклонений х и у от х и у. Коэффициент корреляции знаков колеблется в пределах от -1 до +1. Чем ближе коэффициент к 1, тем теснее связь. Если и > v, то i > 0, так как число согласо­ванных знаков больше, чем несогласованных, и связь пря­мая. При и < v имеем i < 0, потому что число несогласованных знаков больше, чем согласованных, и связь об­ратная. Если и = v, то I=0, и связи нет.

Коэффициент кор­реляции рангов исчисляется не по первичным данным, а по рангам (порядковым номерам), которые присваивают­ся всем значениям изучаемых признаков, расположенным и порядке их возрастания. Если значения признака совпа­дают, то определяется средний ранг путем деления сум­мы рангов на число значений. Коэффициент корреляции рангов определяется по формуле:

(8.35)

где d² — квадрат разности рангов для каждой едини­цы, d =х — у; п — число рангов; s — средний ранг.

Коэффициент корреляции рангов также колеблется в пределах от -1 до +1. Если ранги по обоим признакам совпадают, то зd² =0, значит, р = 1 и, следовательно, связь полная прямая. Если р = -1, связь полная обрат­ная, при р =0 связь между признаками отсутствует.

Коэффициент ассоциации применяется для установления меры связи между двумя качественными альтернативными признаками. Для его вычисления строится комбинационная четырехклеточная таблица, которая выражает связь между двумя альтерна­тивными явлениями.

Коэффициент ассоциации рассчитывается по формуле:

(8.36)

Коэффициент ассоциации также изменяется от -1 до +1. Чем А ближе к единице, тем сильнее связаны между собой изучаемые признаки. При ad> bс связь прямая, а при ad< bс связь обратная, при ad = bс A = 0 и связь отсутствует.

В тех слу­чаях, когда требуется установить связь между качествен­ными признаками, каждый из которых состоит из трех и более групп, применяется коэффициент взаимной сопря­женности.

Различия между условным и безусловным распреде­лением свидетельствуют о влиянии факторного признака на распределение совокупности по результативному при­знаку, т.е. о наличии связи между факторным и результа­тивным признаками, а чем больше эти различия, тем в большей мере признаки связаны между собой, тем теснее связь между ними.

Коэффици­ентом взаимной сопряженности определяется по сле­дующей формуле:

(8.37)

где п — число единиц совокупности; m₁ и т₂ — число групп по первому и второму признакам; ч² — показатель абсолютной квадратической сопряженности Пирсона, ха­рактеризующий близость условных распределений к безусловным, который, как и критерий ч²исчисляется по формуле:

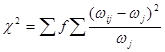(8.38)

где 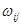. — частости условного распределения в i-й строке; —частости безусловного распределения; j — номер столбца.

Если признаки независимы, то w_ij.. = ., откуда ч² = О и, значит, С = 0. Если же связь функциональная, то коэф­фициент взаимной сопряженности будет равен единице.

Вопросы для теоретического контроля знаний:

1. Определите понятие «статистическая связь».

2. Какие вы знаете формы и методы изучения статистической связи?

3. Укажите основные задачи корреляционно – регрессионного анализа.

4. Каковы определенные значения корреляционного отношения?

5. Что такое множественная корреляция?

6. В чем состоит различие между корреляционной и функциональной связью?

7. Какие основные проблемы решает исследователь при изучении корреляционной зависимости?

8. Какие показатели являются мерой тесноты связи между двумя признаками?

9. Как оценить существенность линейного коэффициента корреляции?

10. Как определяется парная регрессия на основе метода наименьших квадратов и метода группировок?

11. Что такое множественная регрессия?

12. Какое значение имеет расчет индекса корреляции?

13. Какие решения можно принимать на основе уравнения регрессии?

14. Укажите собственно – корреляционные параметрические методы изучения связи. Оценка существенности корреляции

15. Раскройте суть методов изучения связи социальных явлений

16. Какие непараметрические показатели связи вы знаете?

17. Назовите ранговые коэффициенты связи.

18. Для чего рассчитываются частные коэффициенты корреляции?

19. Как подходить к отбору факторов для включения их в уравнение множественной регрессии?

 

Примеры решения задач:

1. По данным о сумме активов и кредитных вложений коммерческих банков необходимо определить направление и тесноту связи между признаками

Таблица 8.1.

Распределение кредитных вложений и сумм активов коммерческих банков

№ п/п	Банк	Кредитные вложения, млрд. руб., х	Сумма активов, млрд. руб., у	Х2	ху	ух
	Комплексбанк					1140,6
	Белорусбанк					1502,5
	Приорбанк					1632,9
	Белбизнесбанк					2007,3
	Белбанк					2191,9
	Белпромстройбанк					2862,4
	Балагропромбанк					3419,4
Итого					14757,0

Сопоставив полученные данные ряда данных х и у, можно наблюдать наличие прямой зависимости между признаками, когда увеличение кредитных вложений увеличивает сумму активов коммерческих банков. Исходя из этого можно сделать вывод, что связь между признаками прямая и ее можно описать уравнением прямой.

Определим параметры уравнения прямой на основе метода наименьших квадратов, решив систему нормальных уравнений:

na₀ + a₁ x = y;

a₀ x +a_{1 x}² = xy.

Получаем:

7а₀ + 8671 а₁ = 14757;

8671а₀ +14266159 а₁ 21956214.

а₀ = 816,2878; а₁ = 1,0429.

Аналитическая связь описывается уравнением:

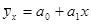
Исходя из полученных результатов получаем:

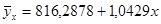
Следовательно, с увеличением кредитных вложений на 1 млрд. руб. сумма активов возрастет на 1,0429 млрд. руб.

2. По данным о сумме активов (у), кредитных вложений (х₁) и величине собственного капитала (х₂) коммерческих банков построить множественное уравнение связи:

 

№ банка	Сумма активов, млрд. руб., у	Кредитные вложения, млрд. руб., х1	Собственный капитал, млрд. руб., х2
Итого

 

Связь предполагается линейная

 

Решение:

 

Таблица 8.2.

Расчетная таблица для определения параметров уравнения регрессии

 

ух1	х21	у2	х1х2	х22	ух2	ух

 

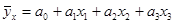
Система нормальных уравнений имеет вид:

 

7а₀ + 8671а₁ + 1046 а₂ = 14757;

8671 а₀ + 14266159 а₁ + 1515415 а₂ = 21956214;

1046а₀ + 1515415а₁ + 175876а₂ = 2534726.

Отсюда: а₀ = -443, 4; а₁ = 0, 0368; а₂ = 16,77;

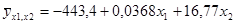
Расчеты показали, что увеличением кредитных вложений на 1 млрд. руб. и собственного капитала коммерческих банков на 1 млрд. руб. стоимость их активов возрастает соответственно на 0, 0368 и 16, 77 млрд. руб.

 

3. По данным задачи 2 оценить тесноту связи между стоимостью активов (у) и кредитными вложениями (х₁), используя различные модификации коэффициента корреляции. Проверить его значимость.

Решение:

Эмпирическое корреляционное отношение:

Задания для самостоятельной работы студентов:

1. Имеются следующие данные:

 

№ серии	Средневзвешенная цена, х	Объем продаж, у
	84,42	79,5
	82,46	279,7
	80,13	71,4
	63,42	242,8
	76,17	76,3
	75,13	74,7
	74,84	210,7
	73,03	75,1
	73,41	75,5
	71,34	335,3

Составьте линейное уравнение регрессии. Вычислите параметры и рассчитайте линейный коэффициент корреляции и корреляционное отношение. Сравните их, сделайте выводы.

2. По данным группировки 40 предприятий легкой промышленности по величине балансовой прибыли и объему произведенной продукции построить уравнение связи (табл. 8.3.)

Таблица 8.3.

Расчетная таблица для определения параметров уравнения регрессии по данным группировки предприятий легкой промышленности по величине балансовой прибыли в 1 квартале 2003г. (цифры условные)

 

Балансовая прибыль, млн. руб.	Объем произведенной продукции, млн. руб.
300-4000	400-500	500-600	600-700	700-800
10-20
20-30
30-40
40-50
50-60

3. Установите направление и характер связи между четырмя факторами по 15 банкам Японии, применив метод приведения параллельных данных:

 

№ банка	Суммарный актив, млрд. долл.	Объем вложений акционеров, млрд. долл.	Чистый доход, млрд. долл.	Депозиты, млрд.долл.
	507,2	19,5	352,9	448,1
	506,6	19,8	187,1	451,9
	487,8	21,1	375,2	447,9
	496,0	18,6	287,9	444,3
	493,6	19,6	444,0	443,2
	458,9	11,7	462,4	411,7
	429,3	10,5	459,5	328,6
	386,9	13,6	511,3	314,7
	311,5	10,8	328,6	259,4
	302,2	10,9	350,0	187,7
	262,0	10,3	298,7	238,5
	242,4	10,6	529,3	269,4
	231,9	8,5	320,0	284,0
	214,3	6,7	502,0	172,3
	208,4	8,3	194,9	166,4

4. Составьте линейное уравнение регрессии зависимости чистого дохода от величины суммарных активов 15 крупнейших банков Японии. Определите параметры уравнения а₀ и а₁. Проанализируйте полученные параметры.

 

№ банка	Суммарный актив, млрд. долл.	Объем вложений акционеров, млрд. долл.	Чистый доход, млрд. долл.	Депозиты, млрд.долл.
	507,2	19,5	352,9	448,1
	506,6	19,8	187,1	451,9
	487,8	21,1	375,2	447,9
	496,0	18,6	287,9	444,3
	493,6	19,6	444,0	443,2
	458,9	11,7	462,4	411,7
	429,3	10,5	459,5	328,6
	386,9	13,6	511,3	314,7
	311,5	10,8	328,6	259,4
	302,2	10,9	350,0	187,7
	262,0	10,3	298,7	238,5
	242,4	10,6	529,3	269,4
	231,9	8,5	320,0	284,0
	214,3	6,7	502,0	172,3
	208,4	8,3	194,9	166,4

Литература:

1. Елисеева И.И., Юзбашев М.М. Общая теория статистики, М.: Финансы и статистика, 1996.- с.190-250, с.708-749.

2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М.: Инфра – М, 2000. –с.221-279, с.298-338.

3. Гусаров В.М. Статистика. М.: ЮНИТА – ДАНА, 2001. –с.181-216.

4. Общая теория статистики под ред.Спирина А.А. М.: Финансы и статистика, 1996.-с.237-278.

5. Статистика: курс лекций под ред. Ионина В.Г. Изд – во НГАЭИУ, М.: Инфра – М, 1997. –с.128-148.

6. Курс социально – экономической статистики под ред. Назарова М.Г. М.: Финстатинформ, Юнита – Дана, 2000. с.708-749.

7. Теория статистики под ред. Шмойловой Р.А. М.: Финансы и статистика, 2002. – с.268 – 332.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: