 |
Математическое ожидание (среднее значение)
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По курсу: «Информатика»
(раздел: «компьютерные технологии вычисления в математическом моделировании»)
Москва, 2010г.
Оглавление
Введение. 5
ЛАБОРАТОРНАЯ РАБОТА № 1 «Статистическая обработка результатов эксперимента» 5
Теоретические сведения. 6
Математическая постановка задачи. 6
Определение значимости коэффициента корреляции. 8
Пример выполнения работы.. 8
Таблица значений критерия Стьюдента. 9
БЛОК-СХЕМА.. 11
ПРОГРАММА НА ЯЗЫКЕ QBASIC.. 12
РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ... 14
ПРИМЕР РАБОТЫ в EXCEL.. 14
Контрольные вопросы.. 15
ЛАБОРАТОРНАЯ РАБОТА № 2 «Численное интегрирование». 15
1. Цель работы. 15
2. Основные теоретические сведения. 16
1). Метод прямоугольников. 16
2) Метод трапеций. 18
3) Метод парабол. 18
3. Порядок выполнения работы.. 19
Пример выполнения работы.. 19
БЛОК-СХЕМА.. 20
ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC.. 22
РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ В Qbasic. 24
Результат расчета в ППП ЭВРИКА. 25
Методические указания к выполнению лабораторной работы на ПК.. 25
Контрольные вопросы.. 26
Варианты заданий для самостоятельного решения. 26
Задание. 26
ЛАБОРАТОРНАЯ РАБОТА № 3 «Уточнение корня уравнения». 29
1. Цель работы.. 29
2. Основные теоретические положения. 29
1). Метод дихотомии. 29
2). Метод касательных. 31
3). Метод простой итерации. 31
4). Метод хорд. 33
3. Порядок выполнения работы.. 34
Пример выполнения лабораторной работы. 35
БЛОК-СХЕМА.. 36
ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC.. 38
РЕЗУЛЬТАТЫ РАБОТЫ В QBASIC.. 41
РЕЗУЛЬТАТЫ РАБОТЫ в Eureka. 42
Контрольные вопросы.. 42
Варианты заданий для самостоятельного решения. 43
Задание. 43
ЛАБОРАТОРНАЯ РАБОТА № 4 «Методы численного решения дифференциальных уравнений. Уравнения 1-го порядка». 48
|
|
|
Цель работы.. 48
Метод Эйлера. 51
Метод Эйлера - Коши. 51
Метод Руге - Кутта. 51
Правило Рунге - Ромберга. 52
Пример решения поставленной задачи. 52
БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ.. 53
ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC.. 55
Построение в Excel графика решений. 58
Контрольные вопросы.. 60
Варианты заданий к лабораторной работе. 62
ЛАБОРАТОРНАЯ РАБОТА № 5 Символьные переменные. 64
Цель работы.. 64
Инструменты обработки текстовых величин. 67
Базовые алгоритмы обработки текста. 75
Сортировка текстовых массивов. 81
Контрольные вопросы.. 93
Варианты заданий для самостоятельного решения. 94
ЛАБОРАТОРНАЯ РАБОТА № 6 Оптимизация технологического процесса. 96
Методы оптимизации функции 1-ой переменной. 96
Цель работы.. 96
Оптимизация функций одной переменной. 96
Методы оптимизации функций одной переменной. 101
Метод поразрядного приближения. 101
Метод дихотомии. 101
Метод Фибоначчи. 102
Метод золотого сечения. 103
Использование ППП Eureka и Excel при решении задач оптимизации. 104
Содержание отчета. 105
Пример выполнения лабораторной работы.. 106
БЛОК-СХЕМА.. 106
ПРОГРАММА НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ QBASIC.. 108
РЕЗУЛЬТАТ в Qbasic. 110
Решение задачи с использованием ППП Eureka. 110
Задания. 111
Контрольные вопросы.. 112
ЛАБОРАТОРНАЯ РАБОТА № 7 Работа с файлами последовательного доступа. 112
Цель работы.. 112
Работа с файлами. 112
Требования к имени файла. 113
Расширение файла. 113
Операции над файлами. 115
Порядок выполнения работы.. 120
Содержание отчета. 121
Пример решения задачи. 121
ПРОГРАММА НА ЯЗЫКЕ QBasic. 122
РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ... 123
Контрольные вопросы.. 124
Варианты заданий к лабораторной работе. 124
Список литературы.. 135
Введение
Широкое внедрение математических методов в самые разнообразные сферы деятельности сегодня уже никого не удивляет. Это не только технические и экономические науки, но и развивающиеся прикладные науки управления: менеджмент, логистика, социально-экономическое прогнозирование и т.д.
|
|
|
Математическое моделирование становится одним из главных направлений в технике, экономике, социологии, биологии и других областях. Поэтому специалистам различных направлений необходимо владеть концепциями и методами математического моделирования, иметь представление об инструментах, применяемых в моделировании.
При изучении курса информатики, студент знакомится с основами алгоритмизации и программирования, с пакетами прикладных программ общего назначения.
Данный лабораторный практикум по курсу «Информатики» включает следующие темы:
1. статистическая обработка результатов эксперимента
2. вычисление интегралов
3. решение нелинейных уравнений
4. решение дифференциальных уравнений
5. оптимизация технологического процессов
6. работа с файлами последовательного доступа
7. символьные переменные.
ЛАБОРАТОРНАЯ РАБОТА № 1
«Статистическая обработка результатов эксперимента»
Цель работы ознакомление с основными характеристиками случайных величин.
В результате эксперимента определились такие показатели, как рост и вес человека.
| рост | х1 | х2 | х3 | ……… | ……… | ……… | ……… Хn |
| вес | Y1 | Y2 | Y3 | ……… | ……… | ……… | ……… Yn |
Обозначим хi – рост, yi – вес. Количество экспериментов- n, где n – размер выборки, i – текущий индекс.
Необходимо определить характеристики случайных величин (величин х и у).
Теоретические сведения
Математическая постановка задачи
(характеристики случайных величин)
Математическое ожидание (среднее значение)
по х: 
по у: 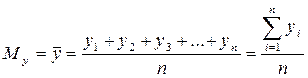
Математическое ожидание характеризует положение случайной величины на числовой оси.
Дисперсия
по х: 
| по у: 
| Где Mx, My – математическое ожидание. |
Дисперсия характеризует разброс случайных величин. В данных формулах – разброс относительно математического ожидания.
|
|
|


