Задача с вертикальными углами 3 глава

I. Традиционная логика весьма изобретательно подо­шла к этим проблемам. Как в огромном разнообразии проблематики мышления найти главное? Следующим об­разом. Мышление интересуется истиной. Истинность или ложность — это качества высказываний, суждений, и толь­ко их. Элементарные суждения утверждают или отрицают какой-то предикат субъектов в форме «все S суть Р», или «ни одно S не есть Р», или «некоторые S суть Р», или «некоторые S не суть Р». Суждения содержат общие понятия — понятия классов. Они — основа всякого мыш­ления. Чтобы суждение было корректно, важно правильна обращаться с его содержанием и объемом. На основе суж­дений делаются умозаключения. Логика изучает формаль­ные условия, при которых заключения оказываются пра­вильными или неправильными. Определенные комбинации суждений позволяют получать «новые» правильные суж­дения. Такие силлогизмы, с их посылками и выводами, являются венцом, самой сутью традиционной логики. Ло-

гика устанавливает различные формы силлогизма, кото­рые гарантируют правильность вывода.

Хотя большинство приводимых в учебниках силлогиз­мов кажутся совершенно бесплодными, как в классиче­ском примере:

Все люди смертны;

Сократ — человек;

Сократ смертен,

встречаются примеры настоящих открытий, которые мо­гут в первом приближении рассматриваться как силло­гизмы, например открытие планеты Нептун. Но и фор­мально, и по существу эти силлогизмы не отличаются друг от друга ¹. Основные правила и характеристики и этих глуповатых, и действительно осмысленных силлогиз­мов совпадают.

Традиционная логика формулирует критерии, кото­рые гарантируют точность, валидность, непротиворечи­вость общих понятий, суждений, выводов и силлогизмов. Основные главы классической логики относятся к этим те­мам. Конечно, иногда правила традиционной логики напо­минают нам эффективные правила дорожного движения.

Если оставить в стороне различия в терминологии и разногласия по второстепенным вопросам, то можно на­звать следующие характерные операции традиционной ло­гики:

Таблица I

определение

сравнение и различение

анализ

абстрагирование

обобщение

классификация

категоризация

образование суждений

умозаключения

составление силлогизмов и т. д. ²

¹ См.: Wertheimer M. Über Schlussprozesse im produktiven Denken. — In: Drei Abhandlungen zur Gestalttheorie. Erlangen Phi­losophische Akademie, 1925, S. 164—184; Ellis W. D. A source book
of gestalt psychology. Selection 23. New York, Harcourt, Brace, 1939.

² Суть этих операций подробно обсуждалась. Для наших целей не имеет значения, определены ли они на менталистском, бихевио-

Эти операции, выделенные, определенные и используе­мые логиками, исследовались и исследуются психологами. В результате возникло много экспериментальных исследо­ваний, посвященных абстрагированию, обобщению, опре­делению, умозаключению и т. д.

Некоторые психологи полагают, что человек умеет мыслить, что он умен, если он может правильно и легко осуществлять операции традиционной логики. Неспособ­ность формировать общие понятия, абстрагировать, делать выводы из силлогизмов определенных формальных типов рассматривается как умственная неполноценность, кото­рая определяется и измеряется в экспериментах ¹.

Как бы ни оценивали мы классическую логику, она обладала и обладает большими достоинствами:

явным стремлением к истине;

сосредоточением внимания на важнейшем различии между простым утверждением, убеждением и точным суждением;

подчеркиванием различия между недостаточно ясными понятиями, туманными обобщениями и точными форму­лировками;

разработкой множества формальных критериев, позво­ляющих обнаружить ошибки, неясности, неправомерные обобщения, поспешные выводы и т. д.;

подчеркиванием важности доказательства;

основательностью правил вывода;

требованием убедительности и строгости каждого от­дельного шага мышления.

Система традиционной логики, основы которой были заложены в «Органоне» Аристотеля, в течение многих веков считалась окончательной; и хотя в нее были вне­сены некоторые уточнения, они не меняли ее основного характера. В период Ренессанса возникла новая область, развитие которой оказало существенное влияние на фор­мирование современной науки. Ее главным достоинством

ристском, прагматическом или каком-либо другом языке, хотя с точки зрения философии существуют большие различия между этими взглядами.

Некоторые современные исследователи считают, что тради­ционная логика не связана с реальным поведением. Это заблужде­ние. Ибо применение логики к поведению можно обосновать примерно следующим образом: поведение будет неразумным, не достигнет цели, приведет к неблагоприятным последствиям, если оно определяется факторами, аналогичными ошибкам в традицион­ной логике.

было введение в качестве фундаментальной новой про­цедуры, которой прежде не придавалось большого значе­ния ввиду ее недостаточной доказательности. Это — метод индукции, с его упором на опыт и экспериментирование. Описание этого метода достигло своего наибольшего со­вершенства в известном каноне правил индукции Джона Стюарта Милля.

Iа. Упор здесь делается не на рациональном выведе­нии из общих положений, а на сборе фактов, эмпириче­ском изучении инвариантных связей между ними и на наблюдении за последствиями изменений, происходящих в реальных ситуациях, — то есть на процедурах, которые приводят к формулировке общих положений ¹. Силлогизмы рассматриваются как инструменты, с помощью которых можно извлечь следствия из таких гипотетических допу­щений с целью их проверки.

Широко известно, что индуктивная логика добавила к классическим правилам и операциям следующее:

Таблица Iа

эмпирические наблюдения

тщательный сбор фактов

эмпирическое изучение проблем

введение экспериментальных методов

корреляция фактов

разработка решающих экспериментов

И. Вторая крупная теория мышления основана на классической теории ассоцианизма. Мышление — это це­почка идей (или в более современных терминах — связь стимулов и реакций или элементов поведения). Способ трактовки мышления ясен: мы должны изучать законы, управляющие последовательностью идей (или в современ­ных терминах — элементов поведения). «Идея» в класси­ческой ассоциативной теории является чем-то вроде следа ощущения, в более современных терминах — копией, сле­дом стимулов. Каков основной закон следования, связи этих элементов? Ответ — подкупающий своей теоретиче­ской простотой — таков: если два предмета а и b часто встречаются вместе, то последующее предъявление а вы-

¹ Главным здесь является изучение корреляции двух рядов разных событий и формулирование законов функционирования, за­менивших простую классификацию.

зовет в субъекте b ¹. Эти элементы связаны между собой, сущности, так же, как номер телефона моего знакомого связан с его именем, или как связаны между собой бес­смысленные слоги в экспериментах по заучиванию серий таких слогов, или как связано слюновыделение у собаки с определенным звуковым сигналом.

Привычка, прошлый опыт, в смысле повторяемости смежных элементов, — скорее инерция, а не разум — та­ковы существенные факторы. Именно это утверждал Дэ­вид Юм. По сравнению с классическим ассоцианизмом эта теория сейчас является очень сложной, но старая идея повторения, смежности все еще остается ее центральным пунктом. Ведущий представитель этого подхода недавно недвусмысленно заявил, что современная теория условных рефлексов имеет, по существу, ту же природу, что и клас­сический ассоцианизм.

Список операций выглядит здесь следующим образом:

Таблица II

ассоциации, приобретенные на основе повторения связи

роль частоты повторения, новизны

припоминание прошлого опыта

пробы и ошибки со случайным успехом

научение на основе повторения успешной пробы

действия в соответствии с условными реакциями и привычками

Эти операции и процессы сейчас широко изучаются с помощью хорошо разработанных методов.

Многие психологи скажут: способность мыслить — это следствие работы ассоциативных связей; ее можно изме­рить количеством ассоциаций, приобретенных субъектом, легкостью и правильностью заучивания и припоминания этих связей ¹.

¹ В дальнейшем развитии науки в этот закон были внесены не­которые уточнения.

См., например: Thorndike E. L. Psychology of arithmetic. New York, Macmillan, 1922, p. 190.

«Педагогика прошлого допускала на практике крупные ошибки, основанные на двух ошибках психологии мышления. Последняя рассматривала рассудок как некую магическую силу или сущность, которая действует вопреки обычным законам научения и противоречитим; и она очень резко отделяла «понимание принципов» с помощью логики от «механической» работы по вычислению... запоминанию фактов и т. п., осуществляемых с помощью простого заучивания и памяти.

Несомненно, и у этого подхода есть свои достоинства, которые касаются очень тонких особенностей, наблюдае­мых в такого рода научении и поведении.

Оба подхода сталкивались с большими трудностями при объяснении осмысленных продуктивных процессов мышления.

Рассмотрим сначала традиционную логику. На протя­жении многих веков вновь и вновь возникало глубокое недовольство тем, как традиционная логика трактовала такие процессы ¹. По сравнению с подлинными, осмыслен­ными, продуктивными процессами проблемы, да и обыч­ные примеры традиционной логики часто выглядят бес­смысленными, плоскими и скучными. Логическая трак­товка, будучи достаточно строгой, все же часто кажется весьма бесплодной, нудной, пустой и непродуктивной.

Рассудок, или анализирующее дискурсивное мышление, вовсе не противостоит законам научения и не независим от них, а явля­ется в действительности необходимым результатом этих законов. Более тщательное изучение анализирующего мышления покажет, что для его объяснения не потребуется никаких иных принципов, кроме законов готовности, тренировки и эффекта; что оно является лишь крайним случаем того, что происходит в процессе ассоциа­тивного научения, описываемого в терминах «поэлементных» дей­ствий...» (см. главу 6).

Аналогичным образом У. Пиллсбери в «Recent naturalistic theo­ries of reasoning» («Scientia», 1924) пишет: «Животное решает за­дачу в результате ряда проб. Почти так же ряд случайных мыслей приводит к решению научной проблемы...» (с. 25). «Никогда нель­зя заранее предсказать, когда будет сделано плодотворное предпо­ложение. Обычно до появления верного предположения будет сде­лан ряд неадекватных. Они могут быть предсказаны другим лицом, даже ребенком или человеком, совершенно незнакомым с пробле­мой. В процессе решения думающий находится в состоянии готов­ности принять предложенное решение.

Его установка очень похожа на ту, которую можно предполо­жить у действующего методом проб и ошибок животного. Эта ус­тановка так же слабо контролируется. В сущности, такой процесс осуществляется методом проб и ошибок и отличается от поведения животного только тем, что пробы в поисках способа преодоления трудностей осуществляются в воображении, а не в реальных дей­ствиях... Это всегда процесс, состоящий из ряда проб и ошибок, ря­да предположений, возникающих по ассоциации» (с. 30). Следует, однако, признать, что в более поздних публикациях Пиллсбери со­вершенно по-иному рассматривал эту ситуацию.

¹ См., например, определенные течения, направленные против традиционной логики, в конце средних веков, или великолепный фрагмент молодого Спинозы «Совершенствование понимания». Это были трагические порывы, порожденные чувством глубокой неудов­летворенности, но и они не привели к созданию действительно конструктивного подхода.

Когда мы пытаемся описать процессы подлинного мыш­ления в терминах традиционной формальной логики, ре­зультат часто оказывается неудовлетворительным: мы имеем ряд корректных операций, но смысл процесса и все, что было в нем живого, убедительного, творческого, как будто исчезают. Можно иметь цепь логических операций, каждая из которых вполне корректна сама по себе, но вместе взятые они не отражают разумный ход мыслей. И действительно, встречаются логически мыслящие люди, которые в определенных ситуациях осуществляют ряд правильных операций, но последние весьма далеки от подлинного полета мыслей. Не следует недооценивать роль традиционной логической тренировки: она ведет к строгости и обоснованности каждого шага, способствует развитию критичности ума, но сама по себе, очевидно, не приводит к продуктивному мышлению ¹. Короче говоря, можно быть пустым и бессмысленным, хотя и точным, и всегда трудно описать подлинно продуктивное мыш­ление.

Кстати, осознание последнего обстоятельства — наряду с другими — привело некоторых логиков к следующему категорическому утверждению: логика, которая занима­ется проблемами правильности и валидности, не имеет ничего общего с реальным продуктивным мышлением. Было также указано, что причина этого состоит в том, что логика не связана с временем и, следовательно, в принципе не имеет дела с процессами актуального мыш­ления, которые вполне реальны и существуют во време­ни. Это разделение оказалось, очевидно, полезным для решения определенных проблем, но с более широкой точ­ки зрения такие утверждения часто напоминают жалобы лисы на незрелость винограда.

Аналогичные трудности возникают и в ассоциативной теории: как отличить разумное мышление от бессмыслен­ных комбинаций, как объяснить творческие стороны мыш­ления ².

Полезное во многих отношениях обсуждение методологии в традиционной логике не может оказать реальной помощи в этом вопросе. См. эвристические идеи (а также логические машины) Буридана, Раймунда Луллия и Джевонса.

В первом отношении характерна блестящая книга Гуго Лип­мана («Über Ideenflucht», 1904).

Обсуждая конкретные примеры «полета мыслей» у душевно­больных, он обнаружил, что критерии, предложенные ассоциатив-

Если решение задачи достигается в результате прос­того припоминания, механического повторения того, что было заучено ранее, благодаря случайному открытию в серии слепых проб, то я бы не решился назвать такой процесс разумным мышлением; и сомнительно, сможет ли нагромождение только таких явлений, пусть даже в больших количествах, создать адекватную картину мысли­тельных процессов. Чтобы как-то объяснить возникнове­ние новых решений, был предложен еще ряд гипотез (на­пример, теория констелляции Зельца, или понятие систем­ной иерархии навыков), которые по самой своей сути оказались почти бесполезными.

В последние десятилетия возникли другие взгляды и понятия, которые открыли новые направления в теории мышления: например, подход гегелевской и марксистской диалектики, подчеркивающий значение динамики разви­тия «внутренних противоречий» и значение трех стадий: тезиса, антитезиса, синтеза; широкое развитие логистики и математической логики (Уайтхед, Рассел и др.), кото­рое обогащает проблематику и методы традиционной ло­гики изучением логики отношений, сетей отношений, ана­лизом форм вывода, отличных от силлогизмов; феномено­логия (Гуссерль), подчеркивающая значение созерцания сущностей в ходе «феноменологической редукции»; праг­матизм (особенно Джона Дьюи) с его подчеркиванием влияния действия и деятельности вместо призрачного мышления, прогресса в настоящем и будущем; а также в психологии — появившаяся одновременно с подходом, опи­сываемым в этой книге, «Denkpsychologie» ¹ Вюрцбургской школы (Кюльпе, Ах, Бюлер, Зельц и др.) с подчеркива­нием влияния «Aufgabe» — роли данной задачи, «мыслей» как «unanschauliche Vorstellungen»² отношений, схем

ной теорией, в действительности недостаточны даже для разграни­чения некоторых видов «пляски идей» от осмысленной речи.

Недавняя формулировка раскрывает основные черты современ­ной формы ассоциативной теории в наиболее сжатом виде. Я ци­тирую статью Кларка Халла «Mind, mechanism and adaptive beha­vior» («Psychological Review», 1937, vol. 44, p. 1—32).

«Корректной, или «правильной», реакцией называется поведе­ние, результат которого подкрепляется. Некорректным, или «оши­бочным», называется поведение, которое тормозится» (с. 15). Мы видим, что главной проблемой является вопрос повторения. Эти важные определения, несомненно, согласуются с духом ассоциатив­ной теории.

¹ Психология мышления (нем.). — Прим. перев.

² Ненаглядные представления (нем.). — Прим. перев.

и т. д.; «натуралистический подход» (Д. Дьюи, У. Пиллсбе­ри и др.), который концентрирует внимание на условиях, дающих толчок продуктивному мышлению в той или иной ситуации.

Большинство из этих подходов важны своими фило­софскими и психологическими аспектами. И хотя они все еще далеки от удовлетворительного решения нашей глав­ной проблемы и упомянутых нами важных вопросов, не­которые из них действительно внесли свой вклад в науку. Другие же снова оказались под влиянием двух классиче­ских подходов. Иными словами, если сквозь новые фор­мулировки мы доберемся до тех операций, из которых они в действительности исходят, то с удивлением обна­ружим, что это, в сущности, те же самые операции двух традиционных подходов. Это напоминает один из тех слу­чаев, которые часто наблюдались в истории логики. Во введении или в какой-нибудь из первых глав книги на­мечается новый подход, совершенно отличный от привыч­ной логической трактовки; действительно, некоторые поло­жения очень напоминают формулировки гештальттеории. Однако, когда дело доходит до конкретного рассмотрения проблемы, вновь всплывают старые операции, старые пра­вила и установки.

Здесь я смог лишь кратко упомянуть эти подходы. Я полагаю, что специалист поймет, что в них соответст­вует нашему подходу и что в корне от него отличается.

Эта книга сосредоточивает внимание на некоторых элементарных, основных вопросах. Природа обсуждаемых проблем позволяет нам рассматривать мышление в тер­минах «относительно закрытых систем», как будто мыш­ление, связанное с решением проблемы, является процес­сом, происходящим независимо от более широкого кон­текста. Только вскользь мы коснемся места, роли и функ­ции такого процесса внутри структуры личности субъекта и внутри структуры его социального поля. Пока же до­статочно отметить, что законы поля, обсуждаемые в этой книге, по-видимому, являются основой адекватной трак­товки этих процессов в пределах более крупных областей.

ГЛАВА 1

Площадь параллелограмма

Среди проблем, над которыми я работал, была задача на определение площади параллелограмма.

Не знаю, получите ли вы от результатов моих опытов такое же удовольствие, какое испытал я. Мне кажется, что получите, если последите за мной, разберетесь в су­ществе проблемы и почувствуете трудности, которые воз­никали на пути и для преодоления которых я должен был находить средства и методы, чтобы психологически уяс­нить выдвинутую проблему.

I

1. Я прихожу в класс. Учитель говорит: «На преды­дущем уроке мы научились определять площадь прямо­угольника. Все ли знают, как это делать?»

Ученики отвечают: «Все». Один из них выкрикивает: «Площадь прямоугольника равняется произведению двух его сторон». Учитель одобряет ответ и затем предлагает несколько задач с различными размерами сторон, которые все были сейчас же решены.

«А теперь, — говорит учитель, — мы пойдем дальше». Он чертит на доске параллелограмм: «Это параллелограмм. Параллелограммом называется плоский четырехугольник, противоположные стороны которого равны и параллель-

Рис. 1

ны». Тут один ученик поднимает руку: «Скажите, пожа­луйста, чему равны стороны?» «О, стороны могут быть самой разной длины, — отвечает учитель. — В данном слу-

чае величина одной из сторон равна 11 дюймам, другой — 5 дюймам». «Тогда площадь равна 5x11 квадратным дюй­мам». «Нет, — говорит учитель, — это неверно. Сейчас вы узнаете, как определяется площадь параллелограмма». Он обозначает вершины буквами а, b, с, d.

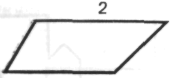
«Я опускаю один перпендикуляр из левого верхнего угла и другой — из правого верхнего угла.

Продолжаю основание вправо.

Обозначаю новые точки буквами e и f».

Рис. 2

С помощью этого чертежа он приступает затем к обычному доказательству теоремы, согласно которой пло­щадь параллелограмма равна произведению основания на высоту, устанавливая равенство некоторых отрезков и уг­лов и равенство двух треугольников. В каждом случав он приводит ранее выученные теоремы, постулаты или ак­сиомы, с помощью которых обосновывает равенство. Нако­нец, он заключает, что теперь доказано, что площадь параллелограмма равна произведению основания на вы­соту.

«Вы найдете доказательство теоремы, которое я вам показал, в своих учебниках на с. 62. Выучите урок дома, тщательно повторите его, чтобы твердо запомнить».

Затем учитель предлагает несколько задач, в ко­торых требуется определить площади параллелограммов различных размеров, с разными сторонами и углами. По­скольку этот класс был «хорошим», задачи были решены правильно. В конце урока учитель задает в качестве до­машнего задания еще десять задач такого же типа.

2.Днем позже я снова оказался в том же классе на следующем уроке.

Урок начался с того, что учитель вызвал ученика и попросил его показать, как определяется площадь парал­лелограмма. Ученик блестяще продемонстрировал это.

Было видно, что он выучил урок. Учитель шепнул мне: «И это не самый лучший из моих учеников. Без сомне­ния, остальные тоже хорошо выучили урок». Письменная контрольная работа дала хорошие результаты.

Многие скажут: «Замечательный класс; цель обучения достигнута». Но, наблюдая за классом, я чувствовал ка­кое-то беспокойство. «Что они выучили? — спросил я се­бя. — Думают ли они вообще? Поняли ли они решение? Не является ли все, что они делают, лишь слепым повто­рением? Безусловно, ученики быстро выполнили все за­дания учителя и, таким образом, усвоили нечто общее. Они могли не только слово в слово повторить сказанное учителем, наблюдался также и некоторый перенос. Но по­няли ли они вообще, в чем тут дело? Как я могу это вы­яснить? Что нужно сделать?»

Я попросил у учителя разрешения задать классу во­прос. «Пожалуйста», — с готовностью ответил учитель.

Я подошел к доске и начертил такую фигуру.

 

Рис. 3 Рис. 4

Некоторые ученики явно растерялись.

Один ученик поднял руку: «Учитель нам этого не объ­яснял».

Остальные занялись задачей. Они срисовали чертеж, провели вспомогательные линии, как их и учили, опустив перпендикуляры из двух верхних углов и продолжив осно­вание (рис. 4). Они были сбиты с толку, озадачены.

Другие же совсем не казались несчастными. Они уве­ренно писали под чертежом: «Площадь равна произведе­нию основания на высоту» — правильное, но, по-видимо­му, совершенно слепое утверждение. Когда же их спро-

сили, могут ли они доказать это с помощью данного чер­тежа, они были весьма озадачены¹.

Третьи вели себя совершенно иначе. Их лица светле­ли, они улыбались и проводили на рисунке следующие линии или поворачивали лист на 45° и тогда выполняли задание (рис. 5А и 5Б).

Рис. 5А Рис. 5Б

Увидев, что только небольшое число учеников справи­лось с задачей, учитель с оттенком неудовольствия сказал мне: «Вы, конечно, предложили им необычный чертеж. Естественно, что они не смогли с ним справиться».

Между нами говоря, не думаете ли и вы: «Не удиви­тельно, что, получив такую незнакомую фигуру, многие не смогли с ней справиться». Но разве она менее знако­ма, чем те вариации первоначальной фигуры, которые да­вал им ранее учитель и с которыми они справились? Учи­тель давал задачи, которые сильно варьировались в от­ношении длины сторон, величины углов и площадей. Эти вариации были явными, и ученикам они вовсе не казались сложными. Вы, быть может, заметили, что мой паралле­лограмм — это просто повернутая первоначальная фигура, предложенная учителем. В отношении всех своих частей она не больше отличается от первоначальной фигуры, чем вариации, предложенные учителем.

¹ Мальчик из другого класса, видя их затруднения, шепнул мне: «В нашем классе проходили задачи с этими перекрывающи­мися фигурами. Тут виноват учитель. Почему он не рассказал, как работать с такими чертежами?» К моему удивлению, именно с этого сложного доказательства иногда начинается изложение в учебниках. Ученикам не только трудно понять его; оно также со­вершенно необязательно для решения задач.

 

Здесь я коротко расскажу об экспериментальной рабо­те с детьми, которых научили определять сначала пло­щадь прямоугольника, а затем площадь параллелограмма (научили проводить вспомогательные линии и получать результат: произведение основания на высоту) и которые знали или не знали доказательство. Потом им задавали вопросы о фигурах, отличавшихся от первоначальной.

Рис. 6

3. Встречаются крайние случаи бессмысленных реак­ций, когда ученик после предъявления такой простой фи­гуры, слепо повторяя слова учителя, бормочет: «Один перпендикуляр из левого верхнего угла», проводит его и затем говорит: «Другой — из правого верхнего угла», про­водит и его, затем: «Продолжить линию основания впра­во» — и, таким образом, получает следующий чертеж:

Рис. 7

4. Однако бывает, что даже шестилетний ребенок, ни­чего не знающий о геометрии, едва знакомый со способом определения площади прямоугольника, находит самостоя­тельно красивое и оригинальное решение для параллело­грамма, хотя его вовсе этому не учили. Некоторые из этих случаев будут описаны в третьей части данной главы.

Бывает также, что, выучив или обнаружив, как опре­деляется площадь параллелограмма, дети, которых просят найти площадь трапеции или любой из приведенных ниже фигур, оказываются вовсе не беспомощными и после неко­торых колебаний, иногда после небольшой подсказки, предлагают прекрасные, подлинные решения типа опи­санных ниже.

Вот эти задания:

Рис. 8

Для всех этих фигур решение возможно посредством осмысленного изменения фигуры (А -ответы), а не слепого и безуспешного применения заученных операций или некоторых из них (В -ответы).

А —ответы

 

Рис. 8А

Испытуемые превращают фигуры в прямоугольники, сдвигая треугольники. Они не дают

В —ответы

 

Рис. 8Б

5. Но остальные дают В -ответы или беспорядочно че­редуют А- и В- ответы. Многие ученики вообще отказы­ваются приступить к решению задач 1, 2 и 3, говоря: «Откуда нам знать? Мы этого не учили».

6. Тогда я провел с детьми эксперимент. Сразу же после демонстрации того, как определяется с помощью вспомогательных линий площадь параллелограмма, я клал

Примеры

А -фигур В -фигур

Рис. 9

перед ними отдельные фигуры или пары А- и B -фигур. В этих парах фигур один из членов пары, B -фигура, не имеет осмысленного A -решения, тогда как для A -фигуры возможно A -решение. Некоторым детям кажется, что А- и B -фигуры не отличаются друг от друга. Все они являются новыми. «Откуда нам знать!» — вот их позиция. Они либо никак не реагируют, либо если и реагируют, то не дифференцируют А- и B -фигуры, проводят вспомо­гательные линии и отвечают наугад.

Другие же последовательно решают A -задачи и иногда через короткое время отвергают B -задачи со словами: «Этого я не могу сделать, я не знаю, чему равна пло­щадь», или даже: «Я не знаю, какова площадь этих не­больших остаточных элементов». В отличие от этих слу­чаев в A -случаях площадь остатков, как правило, не упо­минается; или же ребенок говорит: «Я, конечно, не знаю

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: