 |
Определение коэффициента потерь на трение. Исследования И. Никурадзе
|
|
|
|
Для определения λ при турбулентном режиме предложен ряд эмпирических и полуэмпирических формул, полученных многими авторами в результате исследования различных областей гидравлического трения. Однако фундаментальным исследованием стала работа И. И. Никурадзе, который в 1933 г. опубликовал результаты своих многочисленных опытов, представленных в виде особого графика.
В своих опытах Никурадзе исследовал напорное движение жидкости в круглоцилиндрических трубах, имеющих однозернистую равномерно распределенную (равнозернистую) шероховатость, которую он создавал путем наклеивания калиброванных песчинок высотой Δ на внутреннюю поверхность трубы.
Полученный Никурадзе график представляет собой семейство кривых, построенных в логарифмических координатах (по горизонтальной оси отложены величины lg Re D, а по вертикальной — lg 100λ) по точкам, соответствующим опытам с трубами с различной относительной шероховатостью Δ r = Δ: D, от Δ r = 0,00197 до Δ r = 0,0666.
Рассмотрим подробно график Никурадзе (рисунок 3.20). Все поле графика можно условно разбить на пять областей.
Первая область — область ламинарного режима при Re < 2300, (lg Re≤3,36), здесь все опытные точки независимо от шероховатости уложились на одну прямую линию I, уравнение которой λ = 64 / Re.
Вторая область, расположенная между вертикалями III и IV, — область неустойчивого режима или переходная (числа Рейнольдса лежат в пределах от 2300 до 10000). Здесь возможно существование как ламинарного, так и турбулентного режимов, экспериментальные точки имеют значительный разброс.
Третья область — область гидравлически гладких труб» при турбулентном режиме, здесь толщина вязкого подслоя существенно больше высоты выступов шероховатости и турбулентное ядро потока не соприкасается с ними. Поэтому в этой области коэффициент λ = f (Re) не зависит от шероховатости. Область гладких труб представлена на графике прямой линией II, уравнение которой
|
|
|
. (3.30)
Эта эмпирическая формула была получена Блазиусом в 1913г. в результате обработки многочисленных опытов по исследованию движения жидкости в круглых гладких латунных трубах при числах Рейнольдса Re от 2300 до 100000.
Четвертая область — область турбулентного режима доквадратичного сопротивления шероховатых труб, лежит между прямой II и линией АВ, образованной точками, отделяющими горизонтальные участки кривых с некоторой заданной точностью. Можно видеть, что в этой области каждая кривая отвечает определенному значению относительной шероховатости. Здесь турбулентное ядро постепенно раскрывает шероховатость, поэтому имеет место наиболее общий случай λ = f (Re,Δ r).
Пятая область — область турбулентного режима квадратичного сопротивления шероховатых труб, располагается правее и выше линий АВ. Здесь коэффициент λне зависит от числа Рейнольдса Re (все линии графика — прямые, параллельные горизонтальной оси). Коэффициент λ, а следовательно, и потеря напора hтр зависят от шероховатости λ = f (Δ r). Таким образом, как видно из формулы Вейсбаха - Дарси, для этой области сопротивления потеря напора по длине прямо пропорциональна квадрату средней скорости.
В заключение необходимо отметить, что общий качественный характер зависимостей коэффициента гидравлического трения λ, полученный Никурадзе для труб круглого сечения, распространяется и на другие потоки, в том числе ибезнапорные, что было подтверждено опытами А. П. Зегжды, в которых исследовалось безнапорное движение жидкости в лотке прямоугольного сечения, имеющего различную равнозернистую шероховатость. Важно также подчеркнуть, что после указанных работ отпала необходимость создавать особые расчетные зависимости для различных жидкостей, так как род жидкости учитывается числом Рейнольдса.
|
|
|
3.9.3 Практические способы определения коэффициента гидравлического трения λ для напорных технических труб
Трубы, находящиеся в эксплуатации, подвергаются коррозии и покрываются различными отложениями, имеют разнозернистую шероховатость; выступы шероховатости различной формы и размеров, расстояние между ними неодинаковое (рисунок 3.20).
Опыты, проведенные рядом авторов с техническими трубами, показали, что характер зависимости коэффициента λ от числа Рейнольдса отличается от результатов, полученных Никурадзе, особенно в области доквадратичного сопротивления. Здесь в отличие от графика Никурадзе кривые Δ r = const, опускаясь вниз, постепенно переходят от вида, соответствующего области гладкого сопротивления (где согласно формуле Блазиуса 
), к виду, отвечающему области квадратичного сопротивления. Таким образом, в области доквадратичного сопротивления потеря напора по длине пропорциональна средней скорости υв степени 1,75 < т < 2,0. Такой постепенный переход объясняют тем, что в случае разнозернистой шероховатости при увеличении числа Рейнольдса, а следовательно, уменьшении толщины вязкого подслоя δ выступы шероховатости вступают в соприкосновение с турбулентным потоков не все одновременно, а сначала наиболее высокие, затем средние и только при числах Re, соответствующих квадратичной области сопротивления, вязкий подслой «раскрывает» все выступы шероховатости.
Имея в виду разнозернистую шероховатость, в расчетные зависимости для технических труб вводят некоторую среднюю высоту выступов, именуемую эквивалентной шероховатостью, которую обозначим 
.
При турбулентном режиме для определения коэффициента λ в случае движения жидкости в напорных технических трубах используются или экспериментальные графики, или эмпирические и полуэмпирические формулы. Эти формулы обычно рекомендуются для одной из соответствующих областей сопротивления, приведенных в предыдущем параграфе. Следовательно, прежде чем обращаться к той или иной формуле, необходимо установить область сопротивления, граничными условиями существования которой являются так называемые нижнее 
и верхнее 
предельные числа Рейнольдса.
|
|
|
Согласно А. Д. Альтшулю эти числа могут быть определены по приближенным формулам:
, 
,
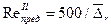где 
.
В случае 10000 < Re < , где Re — число Рейнольдса, соответствующее рассматриваемому потоку, получаем практически область гладких труб, для которой обычно рекомендуются либо формула Л. Прандтля
, (3.31)
или более удобная формула Блазиуса
,
справедливая при числах Рейнольдса Re < 100000.
Область доквадратичного сопротивления отвечает числам Рейнольдса, лежащим в пределах
< Re< .
Для определения коэффициента λв этой области сопротивления рекомендуется обобщенная формула Кольбрука, которую он предложил в 1938 г., основываясь на своих опытах с учетом исследований других авторов
, (3.32)
или более удобная для вычислений формула А. Д. Альтшуля
. (3.33)
В случае Re ≥ имеем квадратичную область сопротивления, для которой формула упрощается и приобретает вид формулы Л. Прандтля для шероховатых труб
, (3.34)
а формула А, Д. Альтшуля (87) приводится к формуле Шифринсона 
.
Величину средней высоты выступов шероховатости , которая входит в расчетные формулы, установить непосредственным измерением практически невозможно, так как на распределение скоростей по сечению и касательные напряжения влияет не только высота выступов, но их форма, а также их шаг расположения на стенке. Поэтому значение для данной трубы находят экспериментально следующим образом. Рассматривая квадратичную область сопротивления опытным путем, пользуясь формулой Вейсбаха-Дарси (3.29), определяют для данной трубы величину λ. Затем по формуле (88) вычисляют искомое значение . Найденную таким образом величину называют эквивалентной шероховатостью, численные значения которой для разных труб приводятся в справочных таблицах.
|
|
|
